2019年 センター試験 数学ⅡB 第2問 微積

2019年センター試験数学ⅡB 第2問微積の解説をします。

まだ問題を解いていない人は解いてから解説を読んでください。

2019年センターⅡB 微積$p,~q$ を実数とし，関数 $f(x)=x^3+px^2+qx$ は $x=-1$ で極値2をとるとする。また，座標平面上の曲線 $y=f(x)$ を $C$，放物線 $y=-kx^2$ を $D$，放物線 $D$ 上の点 $(a,~-ka^2)$ をAとする。ただし，$k>0,~a>0$ である。
(1) 関数 $f(x)$ が $x=-1$ で極値をとるので，$f'(-1)=\myBox{ア}$ である。これと $f(-1)=2$ より，$p=\myBox{イ}$，$q=\myBox{ウエ}$ である。よって，$f(x)$ は $x=\myBox{オ}$ で極小値 $\myBox{カキ}$ をとる。
(2) 点Aにおける放物線 $D$ の接線を $\ell$ とする。$D$ と $\ell$ および $x$ 軸で囲まれた図形の面積 $S$ を $a$ と $k$ を用いて表そう。
　$\ell$ の方程式は

\begin{align*}
y=\myBox{クケ}~kax+ka^{~\myBox{コ}}\cdots\cdots①
\end{align*}

と表せる。$\ell$ と $x$ 軸の交点の $x$ 座標は $\dfrac{\myBox{サ}}{\myBox{シ}}$ であり，$D$ と $x$ 軸および直線 $x=a$ で囲まれた図形の面積は $\dfrac{k}{\myBox{ス}}~a^{~\myBox{セ}}$ である。よって，$S=\dfrac{k}{\myBox{ソタ}}~a^{\mybox{セ}}$ である。
(3) さらに，点Aが曲線 $C$ 上にあり，かつ(2)の接線 $\ell$ が $C$ にも接するとする。このときの(2)の $S$ の値を求めよう。
　Aが $C$ 上にあるので，$k=\dfrac{\mybox{チ}}{\mybox{ツ}}-\mybox{テ}$ である。
　$\ell$ と $C$ の接点の $x$ 座標を $b$ とすると，$\ell$ の方程式は $b$ を用いて

\begin{align*}
y=\mybox{ト}\left(b^2-\mybox{ナ}\right)x-\mybox{ニ}~b^3\cdots\cdots②
\end{align*}

と表される。②の右辺を $g(x)$ とおくと

\begin{align*}
f(x)-g(x)=\left(x-\mybox{ヌ}\right)^2\left(x+\mybox{ネ}~b\right)
\end{align*}

と因数分解されるので，$a=-\myBox{ネ}~b$ となる。①と②の表す直線の傾きを比較することにより，$a^2=\dfrac{\myBox{ノハ}}{\myBox{ヒ}}$ である。
　したがって，求める $S$ の値は $\dfrac{\myBox{フ}}{\myBox{ヘホ}}$ である。

Contents

1 (1)の考え方と解答
2 (2)の考え方と解答
3 (3)の考え方と解答
4 2019年センター数学ⅡB微積を解いた感想

(1)の考え方と解答

ヒロ

一般的に，関数 $f(x)$ が $x=a$ で極値をとるとき，$f'(a)=0$ が成り立つことを利用しよう。

【ア～エの解答】
関数 $f(x)$ が $x=-1$ で極値をとるから，$f'(-1)=0$ である。$f(x)=x^3+px^2+qx$ より

\begin{align*}
f'(x)=3x^2+2px+q
\end{align*}

であるから

\begin{align*}
&3-2p+q=0 \\[4pt]
&2p-q=3
\end{align*}

$f(-1)=2$ より

\begin{align*}
&8+4p+2q=2 \\[4pt]
&2p+q=-3
\end{align*}

よって，$p=0,~q=-3$

ヒロ

次は極小値を求める問題。

ヒロ

いま，$f(x)=x^3-3x$ になっていて，これは奇関数であることに気付けるようにしよう。

ヒロ

つまり，$y=f(x)$ のグラフは原点に関して対称ということ。ということは，$x=-1$ で極値2をとることが分かっているのだから，$x=1$ で極値 $-2$ をとることも分かる。

【オ～キの解答】
$y=f(x)$ は奇関数で，$x^3$ の係数が正だから，$x=1$ で極小値をとることが分かる。よって，極小値は

\begin{align*}
f(1)=1-3=-2
\end{align*}

(2)の考え方と解答

(2) 点Aにおける放物線 $D$ の接線を $\ell$ とする。$D$ と $\ell$ および $x$ 軸で囲まれた図形の面積 $S$ を $a$ と $k$ を用いて表そう。
　$\ell$ の方程式は
\begin{align*}
y=\myBox{クケ}~kax+ka^{~\myBox{コ}}\cdots\cdots①
\end{align*}
と表せる。$\ell$ と $x$ 軸の交点の $x$ 座標は $\dfrac{\myBox{サ}}{\myBox{シ}}$ であり，$D$ と $x$ 軸および直線 $x=a$ で囲まれた図形の面積は $\dfrac{k}{\myBox{ス}}~a^{~\myBox{セ}}$ である。よって，$S=\dfrac{k}{\myBox{ソタ}}~a^{\mybox{セ}}$ である。

ヒロ

放物線 $y=-kx^2$ 上の点における接線 $\ell$ の方程式を求める問題。

ヒロ

2乗に比例する性質を利用して接線の方程式を簡単に求める方法を知っていれば少し楽になる。

【ク～コの解答】
$y’=-2kx$ であるから，$\ell$ の傾きは $-2ka$ である。

\begin{align*}
&y=-2kax+ka^2
\end{align*}

ヒロ

次は接線 $\ell$ と $x$ 軸との交点の $x$ 座標を求める問題。

ヒロ

これは放物線上の2点における接線の交点についての知識があれば，楽勝だね。

【サシの解答】
$x$ 軸も $D$ の接線だから，求める交点の $x$ 座標は

\begin{align*}
\dfrac{0+a}{2}=\dfrac{a}{2}
\end{align*}

である。

ヒロ

次の面積は3分の1公式で求めよう。定積分の式も積分計算も不要になるまで練習しよう。

【スセの解答】
求めるのは次の図の斜線部分の面積である。

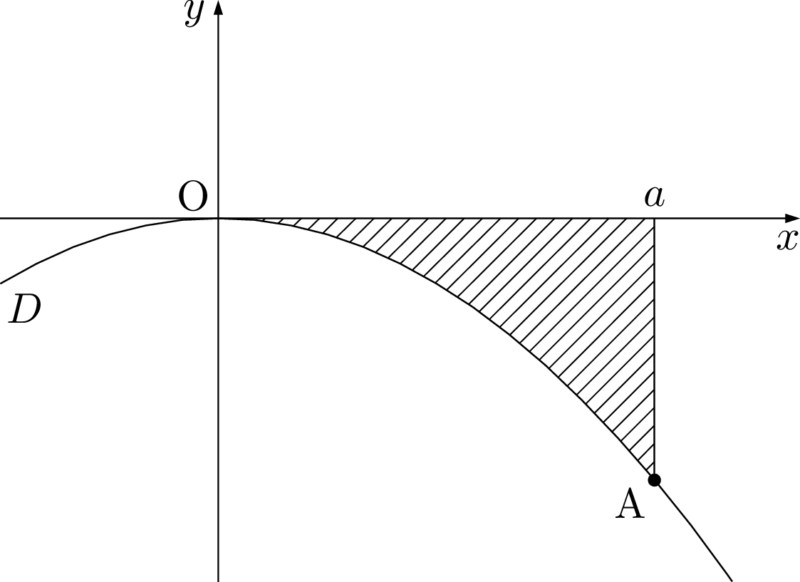
3分の1公式より，求める面積は $\dfrac{k}{3}a^3$ である。

ヒロ

最後の面積 $S$ は12分の1公式を利用しよう。これも定積分の式や積分計算をせずに求められるようにしよう。

【ソタの解答】
$S$ は図の斜線部分の面積である。

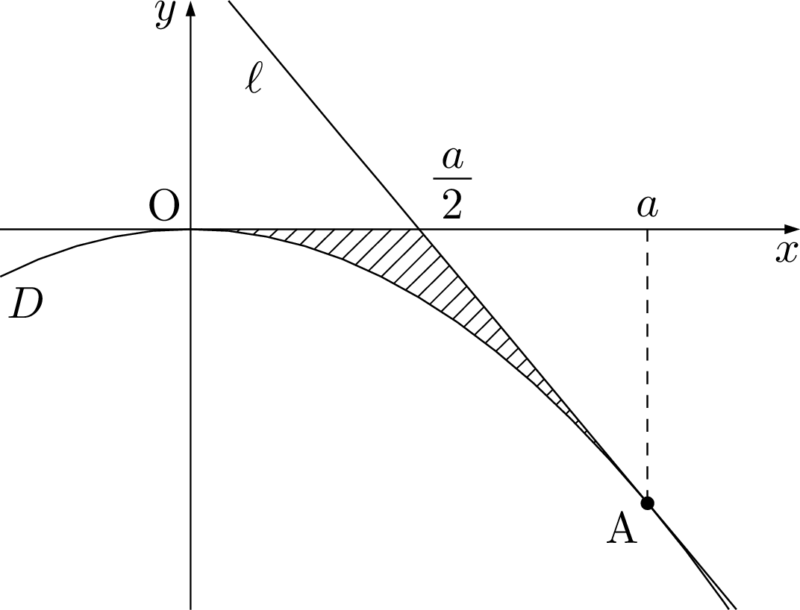
12分の1公式より，$S=\dfrac{k}{12}a^3$

(3)の考え方と解答

(3) さらに，点Aが曲線 $C$ 上にあり，かつ(2)の接線 $\ell$ が $C$ にも接するとする。このときの(2)の $S$ の値を求めよう。
　Aが $C$ 上にあるので，$k=\dfrac{\mybox{チ}}{\mybox{ツ}}-\mybox{テ}$ である。
　$\ell$ と $C$ の接点の $x$ 座標を $b$ とすると，$\ell$ の方程式は $b$ を用いて
\begin{align*}
y=\mybox{ト}\left(b^2-\mybox{ナ}\right)x-\mybox{ニ}~b^3\cdots\cdots②
\end{align*}
と表される。②の右辺を $g(x)$ とおくと
\begin{align*}
f(x)-g(x)=\left(x-\mybox{ヌ}\right)^2\left(x+\mybox{ネ}~b\right)
\end{align*}
と因数分解されるので，$a=-\myBox{ネ}~b$ となる。①と②の表す直線の傾きを比較することにより，$a^2=\dfrac{\myBox{ノハ}}{\myBox{ヒ}}$ である。
　したがって，求める $S$ の値は $\dfrac{\myBox{フ}}{\myBox{ヘホ}}$ である。

ヒロ

点が曲線上にある条件を考えよう。

ヒロ

例えば，点 $(p,~q)$ が曲線 $y=f(x)$ 上にあるとき，$q=f(p)$ が成り立つ。

【チ～テの解答】
点 $\mathrm{A}(a,~-ka^2)$ が$C:y=x^3-3x$ 上にあるから

\begin{align*}
&-ka^2=a^3-3a \\[4pt]
&k=\dfrac{3}{a}-a
\end{align*}

ヒロ

$\ell$ が $C$ にも接していて，その接点の $x$ 座標を $b$ としたときの $\ell$ の方程式を求める問題。

ヒロ

単純に，$C$ 上の点で $x$ 座標が $b$ である点における接線の方程式を求めれば良いね。

【ト～ニの解答】
$C:y=x^3-3x$ より，$y’=3x^2-3$ であるから，$\ell$ の方程式は次のようになる。

\begin{align*}
&y=(3b^2-3)(x-b)+b^3-3b \\[4pt]
&y=3(b^2-1)x-2b^3
\end{align*}

ヒロ

次は $f(x)-g(x)$ を因数分解する問題。

ヒロ

$C:y=f(x)$ は3次関数で，$\ell:y=g(x)$ は $C$ 上の点 $(b,~f(b))$ における接線ということを利用して，なるべく少ない時間で因数分解しよう。

【ヌネの解答】
まず，$x=b$ で接しているから，$f(x)-g(x)=0$ は $x=b$ を重解としてもつ，すなわち $f(x)-g(x)$ は $(x-b)^2$ を因数にもつことが分かる。また，$C$ の変曲点が原点だから，3次関数の等間隔性によって，$C$ と $\ell$ の交点のうち，接点以外の点の $x$ 座標が $-2b$ であることも分かる。したがって，

\begin{align*}
f(x)-g(x)=(x-b)^2(x+2b)
\end{align*}

ヒロ

ここで，問題文から，$f(x)-g(x)$ が因数分解されたことによって，$a=-2b$ となることが分かると読み取れるけど，すぐに理解できない人は，「何故こうなるんだろう？」と考えてはいけない。

ヒロ

仮に5分考えて理由が分かったとしても，1点も増えないし，ただ時間を浪費するだけなので得るものはほとんどない。

ヒロ

練習として，この問題を解いていたとしても，全部解き終わってからじっくり考えるようにしよう。

【 $a=-2b$ である理由】
いま，点Aは $C$ 上にもあり，$\ell$ 上にもある。点Aの $x$ 座標は $a$ だから，$f(a)=g(a)$ が成り立つ。よって，

\begin{align*}
f(x)-g(x)=(x-b)^2(x+2b)
\end{align*}

に $x=a$ を代入すると

\begin{align*}
&f(a)-g(a)=(a-b)^2(a+2b) \\[4pt]
&(a-b)^2(a+2b)=0
\end{align*}

ここで，どう考えても $\ell$ と $C$ の接点が点Aにはならない（グラフを参照）から，$a\neq b$ であり，$a=-2b$ となる。

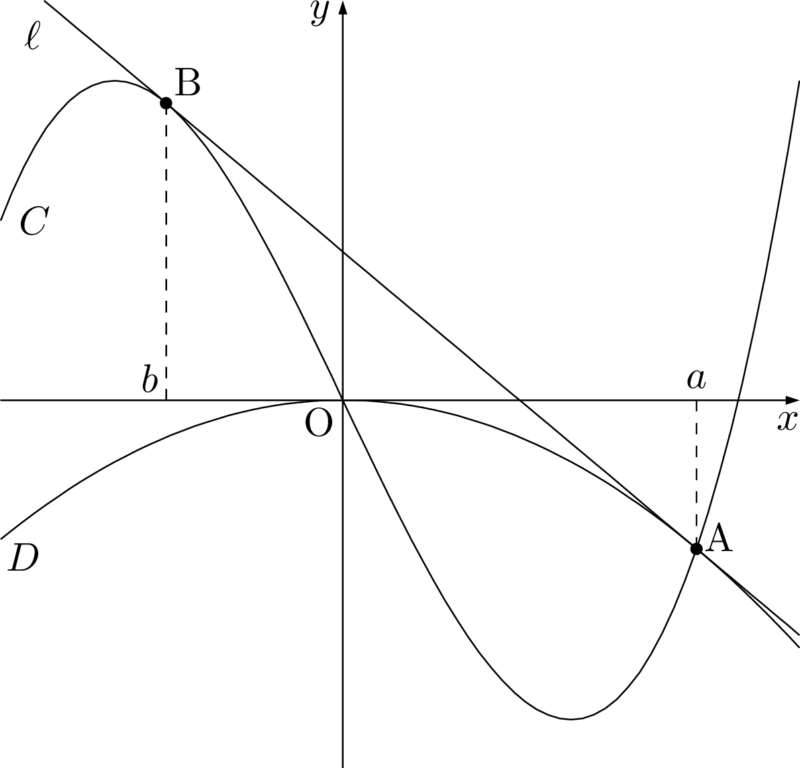
また，このことは3次関数の接点・変曲点・もう1つの交点に関する $1:2$ の法則からも $a=-2b$ となることは明らかである。

ヒロ

次は問題文の誘導通りに①と②の表す傾きを比較しよう。

【ノ～ヒの解答】
①と②より

\begin{align*}
&-2ka=3(b^2-1) \\[4pt]
&-2\left(\dfrac{3}{a}-a\right)a=3\left\{\left(-\dfrac{1}{2}a\right)^2-1\right\} \\[4pt]
&-6+2a^2=\dfrac{3}{4}a^2-3 \\[4pt]
&\dfrac{5}{4}a^2=3 \\[4pt]
&a^2=\dfrac{12}{5}
\end{align*}

ヒロ

最後は(2)で求めた式を利用して $S$ の値を求めよう。

【フ～ホの解答】

\begin{align*}
S&=\dfrac{1}{12}a^2\times ka \\[4pt]
&=\dfrac{1}{12}a^2(3-a^2) \\[4pt]
&=\dfrac{1}{12}\Cdota\dfrac{12}{5}\Cdota\left(3-\dfrac{12}{5}\right) \\[4pt]
&=\dfrac{3}{25}
\end{align*}