Contents
アステロイド曲線で囲まれる部分の面積

ヒロ
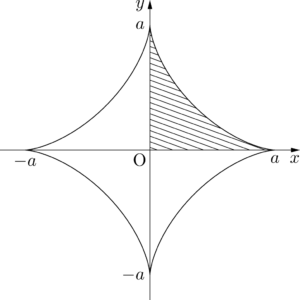
アステロイド曲線で囲まれる部分の面積 $S$ を求めよう。
斜線部分の面積の4倍が $S$ である。

\begin{align*}
S&=4\dint{0}{a}y\;dx \\[4pt]
&=4\dint{\frac{\pi}{2}}{0}y\dfrac{dx}{d\theta}\;d\theta \\[4pt]
&=4\dint{\frac{\pi}{2}}{0}a\sin^3\theta\cdot3a\cos^2\theta(-\sin\theta)\;d\theta \\[4pt]
&=12a^2\dint{0}{\frac{\pi}{2}}\sin^4\theta\cos^2\theta\;d\theta \\[4pt]
&=12a^2\dint{0}{\frac{\pi}{2}}(\sin^4\theta-\sin^6\theta)\;d\theta
\end{align*}
ここで $I_n=\dint{0}{\frac{\pi}{2}}\sin^n\theta\;d\theta$ とおくとS&=4\dint{0}{a}y\;dx \\[4pt]
&=4\dint{\frac{\pi}{2}}{0}y\dfrac{dx}{d\theta}\;d\theta \\[4pt]
&=4\dint{\frac{\pi}{2}}{0}a\sin^3\theta\cdot3a\cos^2\theta(-\sin\theta)\;d\theta \\[4pt]
&=12a^2\dint{0}{\frac{\pi}{2}}\sin^4\theta\cos^2\theta\;d\theta \\[4pt]
&=12a^2\dint{0}{\frac{\pi}{2}}(\sin^4\theta-\sin^6\theta)\;d\theta
\end{align*}
\begin{align*}
S=12a^2(I_4-I_6)
\end{align*}
と表すことができる。S=12a^2(I_4-I_6)
\end{align*}

ヒロ
$I_4$ や $I_6$ を求めるのではなく,$I_n$ を $n$ で表した方が,書く量は少ないと思うので,一般的に求めた方が良い。

ヒロ
前回の記事で求めているから,ここではその過程を省略する。
\begin{align*}
S&=12a^2\left(\dfrac{3}{4}\cdot\dfrac{1}{2}\cdot\dfrac{\pi}{2}
-\dfrac{5}{6}\Cdota\dfrac{3}{4}\Cdota\dfrac{1}{2}\Cdota\dfrac{\pi}{2}\right) \\[4pt]
&=12a^2\Cdota\dfrac{1}{6}\Cdota\dfrac{3}{4}\Cdota\dfrac{1}{2}\Cdota\dfrac{\pi}{2} \\[4pt]
&=\dfrac{3}{8}\pi a^2
\end{align*}
S&=12a^2\left(\dfrac{3}{4}\cdot\dfrac{1}{2}\cdot\dfrac{\pi}{2}
-\dfrac{5}{6}\Cdota\dfrac{3}{4}\Cdota\dfrac{1}{2}\Cdota\dfrac{\pi}{2}\right) \\[4pt]
&=12a^2\Cdota\dfrac{1}{6}\Cdota\dfrac{3}{4}\Cdota\dfrac{1}{2}\Cdota\dfrac{\pi}{2} \\[4pt]
&=\dfrac{3}{8}\pi a^2
\end{align*}
アステロイド曲線の長さ

ヒロ
アステロイド曲線の長さを求めよう。

ヒロ
面積のときと同様に,第1象限の部分の長さを求めて4倍すればよい。
$\dfrac{dx}{d\theta},~\dfrac{dy}{d\theta}$ は
よって
\begin{align*}
\begin{cases}
\dfrac{dx}{d\theta}=-3a\cos^2\theta\sin\theta \\[4pt]
\dfrac{dy}{d\theta}=3a\sin^2\theta\cos\theta
\end{cases}
\end{align*}
となるから\begin{cases}
\dfrac{dx}{d\theta}=-3a\cos^2\theta\sin\theta \\[4pt]
\dfrac{dy}{d\theta}=3a\sin^2\theta\cos\theta
\end{cases}
\end{align*}
\begin{align*}
&\sqrt{\left(\dfrac{dx}{d\theta}\right)^2+\left(\dfrac{dy}{d\theta}\right)^2} \\[4pt]
&=\sqrt{9a^2\cos^4\theta\sin^2\theta+9a^2\sin^4\theta\cos^2\theta} \\[4pt]
&=\sqrt{9a^2\sin^2\theta\cos^2\theta(\cos^2\theta+\sin^2\theta)} \\[4pt]
&=\abs{3a\sin\theta\cos\theta} \\[4pt]
&=\dfrac{3}{2}a\abs{\sin2\theta}
\end{align*}
$0\leqq \theta\leqq\dfrac{\pi}{2}$ のとき,$0\leqq2\theta\leqq\pi$ であるから,$\sin2\theta\geqq0$&\sqrt{\left(\dfrac{dx}{d\theta}\right)^2+\left(\dfrac{dy}{d\theta}\right)^2} \\[4pt]
&=\sqrt{9a^2\cos^4\theta\sin^2\theta+9a^2\sin^4\theta\cos^2\theta} \\[4pt]
&=\sqrt{9a^2\sin^2\theta\cos^2\theta(\cos^2\theta+\sin^2\theta)} \\[4pt]
&=\abs{3a\sin\theta\cos\theta} \\[4pt]
&=\dfrac{3}{2}a\abs{\sin2\theta}
\end{align*}
よって
\begin{align*}
\sqrt{\left(\dfrac{dx}{d\theta}\right)^2+\left(\dfrac{dy}{d\theta}\right)^2}=\dfrac{3}{2}a\sin2\theta
\end{align*}
したがって,求めるアステロイド曲線の長さを $L$ とすると\sqrt{\left(\dfrac{dx}{d\theta}\right)^2+\left(\dfrac{dy}{d\theta}\right)^2}=\dfrac{3}{2}a\sin2\theta
\end{align*}
\begin{align*}
L&=4\dint{0}{\frac{\pi}{2}}\sqrt{\left(\dfrac{dx}{d\theta}\right)^2+\left(\dfrac{dy}{d\theta}\right)^2}\;d\theta \\[4pt]
&=4\dint{0}{\frac{\pi}{2}}\dfrac{3}{2}a\sin2\theta\;d\theta \\[4pt]
&=3a\tint{-\cos2\theta}{0}{\frac{\pi}{2}} \\[4pt]
&=6a
\end{align*}
L&=4\dint{0}{\frac{\pi}{2}}\sqrt{\left(\dfrac{dx}{d\theta}\right)^2+\left(\dfrac{dy}{d\theta}\right)^2}\;d\theta \\[4pt]
&=4\dint{0}{\frac{\pi}{2}}\dfrac{3}{2}a\sin2\theta\;d\theta \\[4pt]
&=3a\tint{-\cos2\theta}{0}{\frac{\pi}{2}} \\[4pt]
&=6a
\end{align*}