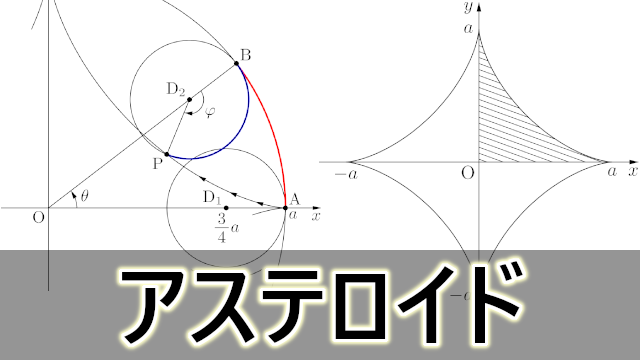
Contents
アステロイド曲線の方程式

ヒロ
極座標を直交座標に置き換えて,$x,~y$ が満たす方程式を考えてみよう。
$\cos^2\theta+\sin^2\theta=1$ より
\begin{align*}
&\left(a\cos^3\theta\right)^{\frac23}+\left(a\sin^3\theta\right)^{\frac23}=a^{\frac23} \\[4pt]
&x^{\frac23}+y^{\frac23}=a^{\frac23}
\end{align*}
&\left(a\cos^3\theta\right)^{\frac23}+\left(a\sin^3\theta\right)^{\frac23}=a^{\frac23} \\[4pt]
&x^{\frac23}+y^{\frac23}=a^{\frac23}
\end{align*}
アステロイド曲線の描画

ヒロ
媒介変数表示されたアステロイド曲線を描こう。

ヒロ
対称性を考慮すれば,調べる範囲を狭くできるが,ここでは $0\leqq\theta\leqq2\pi$ の範囲の増減表を書いておく。
$\begin{cases}
x=a\cos^3\theta \\[4pt]
y=a\sin^3\theta
\end{cases}$より,
$\dfrac{dx}{d\theta}=0$ とすると,
x=a\cos^3\theta \\[4pt]
y=a\sin^3\theta
\end{cases}$より,
\begin{align*}
\begin{cases}
\dfrac{dx}{d\theta}=-3a\cos^2\theta\sin\theta \\[4pt]
\dfrac{dy}{d\theta}=3a\sin^2\theta\cos\theta
\end{cases}
\end{align*}
\begin{cases}
\dfrac{dx}{d\theta}=-3a\cos^2\theta\sin\theta \\[4pt]
\dfrac{dy}{d\theta}=3a\sin^2\theta\cos\theta
\end{cases}
\end{align*}
$\dfrac{dx}{d\theta}=0$ とすると,
\begin{align*}
\theta=0,~\dfrac{\pi}{2},~\pi,~\dfrac{3}{2}\pi,~2\pi
\end{align*}
$\dfrac{dy}{d\theta}=0$ とすると,\theta=0,~\dfrac{\pi}{2},~\pi,~\dfrac{3}{2}\pi,~2\pi
\end{align*}
\begin{align*}
\theta=0,~\dfrac{\pi}{2},~\pi,~\dfrac{3}{2}\pi,~2\pi
\end{align*}
よって,増減は次のようになる。\theta=0,~\dfrac{\pi}{2},~\pi,~\dfrac{3}{2}\pi,~2\pi
\end{align*}
\begin{align*}
\begin{array}{|c||c|c|c|c|c|c|c|c|c|}\hline
\theta & 0 & \cdots & \dfrac{\pi}{2} & \cdots & \pi & \cdots & \dfrac{3}{2}\pi & \cdots & 2\pi \\\hline
\dfrac{dx}{d\theta} & 0 & – & 0 & – & 0 & + & 0 & + & 0 \\\hline
\dfrac{dy}{d\theta}& 0 & + & 0 & – & 0 & – & 0 & + & 0 \\\hline
(x,~y) & (a,~0) & \nwarrow & (0,~a) & \swarrow & (-a,~0) & \searrow & (0,~-a) & \nearrow & (a,~0) \\\hline
\end{array}
\end{align*}
ここで\begin{array}{|c||c|c|c|c|c|c|c|c|c|}\hline
\theta & 0 & \cdots & \dfrac{\pi}{2} & \cdots & \pi & \cdots & \dfrac{3}{2}\pi & \cdots & 2\pi \\\hline
\dfrac{dx}{d\theta} & 0 & – & 0 & – & 0 & + & 0 & + & 0 \\\hline
\dfrac{dy}{d\theta}& 0 & + & 0 & – & 0 & – & 0 & + & 0 \\\hline
(x,~y) & (a,~0) & \nwarrow & (0,~a) & \swarrow & (-a,~0) & \searrow & (0,~-a) & \nearrow & (a,~0) \\\hline
\end{array}
\end{align*}
\begin{align*}
\dfrac{dy}{dx}&=\dfrac{3a\sin^2\theta\cos\theta}{-3a\cos^2\theta\sin\theta} =-\tan\theta
\end{align*}
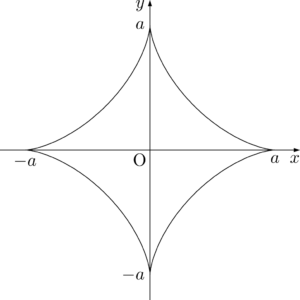
であることを考えると,アステロイドのグラフは図のようになる。\dfrac{dy}{dx}&=\dfrac{3a\sin^2\theta\cos\theta}{-3a\cos^2\theta\sin\theta} =-\tan\theta
\end{align*}


ヒロ
増減だけでは凹凸が分からないため,円のようなグラフを描いてしまうかもしれない。正しく描くために $\dfrac{dy}{dx}$ を考えることで,凹凸が分かる。
例えば,点 $(a,~0)$ では $\dfrac{dy}{dx}=0$ となるから,曲線は $x$ 軸に接していることが分かる。$\theta$ を増加させていくと,点 $(0,~a)$ では $\dfrac{dy}{dx}=\dlim{\theta\to\frac{\pi}{2}-0}(-\tan\theta)=-\infty$ となるから,曲線は $y$ 軸に接していることが分かる。