Contents
2直線のなす角とタンジェントの加法定理

ヒロ
直線と $x$ 軸のなす角とタンジェントの関係を理解することができれば,2直線のなす角とタンジェントの加法定理についても簡単に理解できるだろう。
【2直線のなす角】
2直線 $l:y=ax+b$,$m:y=cx+d$ と $x$ 軸の正の方向とのなす角をそれぞれ $\alpha$,$\beta$$(\alpha<\beta)$ とし,$l,~m$ のなす鋭角を $\theta$ とすると
$\alpha-\beta$ と $\pi-(\alpha-\beta)$ のうち,鋭角である方が $\theta$ である。$\alpha-\beta$ が鋭角のときは,$\theta=\alpha-\beta$ となり,$\pi-(\alpha-\beta)$ が鋭角のときは,$\theta=\pi-(\alpha-\beta)$ となる。
一般に,$\tan(\pi-x)=-\tan x$ が成り立つから,
2直線 $l:y=ax+b$,$m:y=cx+d$ と $x$ 軸の正の方向とのなす角をそれぞれ $\alpha$,$\beta$$(\alpha<\beta)$ とし,$l,~m$ のなす鋭角を $\theta$ とすると
\begin{align*} \alpha-\beta=\theta,~\pi-\theta \end{align*}
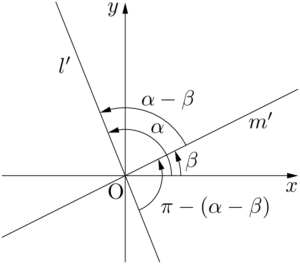
が成り立つ。これについては,2直線が原点を通るように平行移動した2直線 $l’,~m’$ のなす角を考えると理解しやすいだろう。平行移動しているから,2直線 $l’,~m’$ と $x$ 軸の正の方向となす角はそれぞれ $\alpha,~\beta$ である。
$\alpha-\beta$ と $\pi-(\alpha-\beta)$ のうち,鋭角である方が $\theta$ である。$\alpha-\beta$ が鋭角のときは,$\theta=\alpha-\beta$ となり,$\pi-(\alpha-\beta)$ が鋭角のときは,$\theta=\pi-(\alpha-\beta)$ となる。
一般に,$\tan(\pi-x)=-\tan x$ が成り立つから,
\begin{align*} &\tan\theta=\pm\tan(\alpha-\beta) \end{align*}
となる。よって \begin{align*} \tan\theta=\abs{\tan(\alpha-\beta)} \end{align*}
となるから,加法定理を用いて右辺を計算することで $\tan\theta$ の値を求めることができ,$\theta$ も求めることができる。2直線のなす角に関する問題
2020年 立教大座標平面において,2直線 $x+2y-4=0$,$-3x+4y+1=0$ のなす角を $\theta$ とするとき,$\cos\theta=\myhako$ である。ただし,$0<\theta<\dfrac{\pi}{2}$ とする。
【考え方と解答】
2直線 $x+2y-4=0$,$-3x+4y+1=0$ と $x$ 軸のなす角をそれぞれ $\alpha,~\beta$ とすると,
2直線 $x+2y-4=0$,$-3x+4y+1=0$ と $x$ 軸のなす角をそれぞれ $\alpha,~\beta$ とすると,
\begin{align*} \tan\alpha=-\dfrac{1}{2},~\tan\beta=\dfrac{3}{4} \end{align*}
となる。よって \begin{align*} \tan\theta&=\abs{\tan(\alpha-\beta)} \\[4pt] &=\abs{\dfrac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}} \\[4pt] &=\abs{\dfrac{-\dfrac{1}{2}-\dfrac{3}{4}}{1+\left(-\dfrac{1}{2}\right)\Cdota\dfrac{3}{4}}} \\[4pt] &=\abs{\dfrac{-4-6}{8-3}}=2 \end{align*}
$1+\tan^2\theta=\dfrac{1}{\cos^2\theta}$ より \begin{align*} \cos^2\theta&=\dfrac{1}{1+\tan^2\theta} \\[4pt] &=\dfrac{1}{1+2^2}=\dfrac{1}{5} \end{align*}
$0<\theta<\dfrac{\pi}{2}$ のとき,$\cos\theta>0$ であるから,$\cos\theta=\dfrac{1}{\sqrt{5}}$
ヒロ
空欄を埋めるだけなので,次のように求めても良い。
【別の考え方と解答】
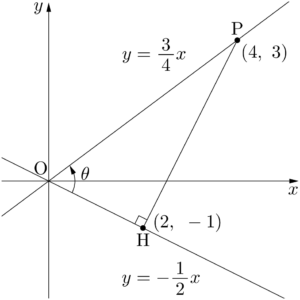
2直線が原点を通るように平行移動すると,2直線は $y=-\dfrac{1}{2}x$,$y=\dfrac{3}{4}x$ となり,これらのなす角が $\theta$ となる。

上図において,$\cos\theta$ を求めれば良いから,$y=\dfrac{3}{4}x$ 上の点Pを適当に定め,$y=-\dfrac{1}{2}x$ に垂線PHを下ろして,直角三角形OPHを考える。点Pの座標をP$(4,~3)$ とすると,点Pを通り,$y=-\dfrac{1}{2}x$ に垂直な直線の方程式は $y=2x-5$ となる。
$y=2x-5$ と $y=-\dfrac{1}{2}x$ を連立して $y$ を消去すると
OPとOHの長さを求めると
2直線が原点を通るように平行移動すると,2直線は $y=-\dfrac{1}{2}x$,$y=\dfrac{3}{4}x$ となり,これらのなす角が $\theta$ となる。

上図において,$\cos\theta$ を求めれば良いから,$y=\dfrac{3}{4}x$ 上の点Pを適当に定め,$y=-\dfrac{1}{2}x$ に垂線PHを下ろして,直角三角形OPHを考える。点Pの座標をP$(4,~3)$ とすると,点Pを通り,$y=-\dfrac{1}{2}x$ に垂直な直線の方程式は $y=2x-5$ となる。
$y=2x-5$ と $y=-\dfrac{1}{2}x$ を連立して $y$ を消去すると
\begin{align*}
&2x-5=-\dfrac{1}{2}x \\[4pt]
&4x-10=-x \\[4pt]
&x=2
\end{align*}
このとき,$y=-1$ となるから,Hの座標はH$(2,~-1)$ である。&2x-5=-\dfrac{1}{2}x \\[4pt]
&4x-10=-x \\[4pt]
&x=2
\end{align*}

OPとOHの長さを求めると
\begin{align*}
&\text{OP}=\sqrt{4^3+3^2}=5 \\[4pt]
&\text{OQ}=\sqrt{2^2+(-1)^2}=\sqrt{5}
\end{align*}
となるから,&\text{OP}=\sqrt{4^3+3^2}=5 \\[4pt]
&\text{OQ}=\sqrt{2^2+(-1)^2}=\sqrt{5}
\end{align*}
\begin{align*}
\cos\theta=\dfrac{\text{OH}}{\text{OP}}=\dfrac{\sqrt{5}}{5}
\end{align*}
\cos\theta=\dfrac{\text{OH}}{\text{OP}}=\dfrac{\sqrt{5}}{5}
\end{align*}


















