Contents
2直線のなす角に関する問題
2020年 近畿大$k$ を正の実数とする。座標平面上において,方程式
$l$ と $x$ 軸との交点をB,$m$ と $x$ 軸との交点をCとすると,$\kaku{BAC}=\dfrac{\pi}{3}$ のとき,$k=\dfrac{\myhako+\myhako\sqrt{\myhako}}{\myhako}$ である。
\begin{align*}
16kx^2+(8k-8)xy-4y^2-(8k^2+42k)x-(4k^2-21)y+21k^2=0
\end{align*}
は2つの直線16kx^2+(8k-8)xy-4y^2-(8k^2+42k)x-(4k^2-21)y+21k^2=0
\end{align*}
\begin{align*}
&l:\myhako\,kx-y-k^2=0 \\[4pt]
&m:\myhako\,x+\myhako\,y-21=0
\end{align*}
を表す。$l$ と $m$ の交点をAとする。&l:\myhako\,kx-y-k^2=0 \\[4pt]
&m:\myhako\,x+\myhako\,y-21=0
\end{align*}
$l$ と $x$ 軸との交点をB,$m$ と $x$ 軸との交点をCとすると,$\kaku{BAC}=\dfrac{\pi}{3}$ のとき,$k=\dfrac{\myhako+\myhako\sqrt{\myhako}}{\myhako}$ である。
【前半の問題の考え方と解答】
与えられた方程式を因数分解して,2直線の方程式を求めよう。与えられた方程式より
与えられた方程式を因数分解して,2直線の方程式を求めよう。与えられた方程式より
\begin{align*}
&16kx^2+\{(8k-8)y-(8k^2+42k)\}x-\{4y^2+(4k^2-21)y-21k^2\}=0 \\[4pt]
&16kx^2+\{(8k-8)y-(8k^2+42k)\}x-(y+k^2)(4y-21)=0 \\[4pt]
&\{2kx-(y+k^2)\}(8x+4y-21)=0 \\[4pt]
&2kx-y-k^2=0~または~8x+4y-21=0
\end{align*}
よって,与えられた方程式は2直線&16kx^2+\{(8k-8)y-(8k^2+42k)\}x-\{4y^2+(4k^2-21)y-21k^2\}=0 \\[4pt]
&16kx^2+\{(8k-8)y-(8k^2+42k)\}x-(y+k^2)(4y-21)=0 \\[4pt]
&\{2kx-(y+k^2)\}(8x+4y-21)=0 \\[4pt]
&2kx-y-k^2=0~または~8x+4y-21=0
\end{align*}
\begin{align*}
&l:2kx-y-k^2=0 \\[4pt]
&m:8x+4y-21=0
\end{align*}
を表す。&l:2kx-y-k^2=0 \\[4pt]
&m:8x+4y-21=0
\end{align*}

ヒロ
次は2直線のなす角に関する問題だから,タンジェントの加法定理を利用しよう。
【後半の問題の考え方と解答】
2直線 $l,~m$ と $x$ 軸の正の方向となす角をそれぞれ $\alpha,~\beta$ とすると
2直線 $l,~m$ と $x$ 軸の正の方向となす角をそれぞれ $\alpha,~\beta$ とすると
\begin{align*}
\tan\alpha=2k,~\tan\beta=-2
\end{align*}
が成り立つ。$\kaku{BAC}=\beta-\alpha$ より,\tan\alpha=2k,~\tan\beta=-2
\end{align*}
\begin{align*}
&\tan(\beta-\alpha)=\dfrac{\tan\beta-\tan\alpha}{1+\tan\beta\tan\alpha} \\[4pt]
&\tan\dfrac{\pi}{3}=\dfrac{-2-2k}{1+(-2)\Cdota2k} \\[4pt]
&\sqrt{3}(1-4k)=-2-2k \\[4pt]
&(4\sqrt{3}-2)k=\sqrt{3}+2 \\[4pt]
&k=\dfrac{\sqrt{3}+2}{4\sqrt{3}-2}
\end{align*}
分母・分子に $4\sqrt{3}+2$ をかけて&\tan(\beta-\alpha)=\dfrac{\tan\beta-\tan\alpha}{1+\tan\beta\tan\alpha} \\[4pt]
&\tan\dfrac{\pi}{3}=\dfrac{-2-2k}{1+(-2)\Cdota2k} \\[4pt]
&\sqrt{3}(1-4k)=-2-2k \\[4pt]
&(4\sqrt{3}-2)k=\sqrt{3}+2 \\[4pt]
&k=\dfrac{\sqrt{3}+2}{4\sqrt{3}-2}
\end{align*}
\begin{align*}
k&=\dfrac{(\sqrt{3}+2)(4\sqrt{3}+2)}{(4\sqrt{3}-2)(4\sqrt{3}+2)} \\[4pt]
&=\dfrac{16+10\sqrt{3}}{44} \\[4pt]
&=\dfrac{8+5\sqrt{3}}{22}
\end{align*}
k&=\dfrac{(\sqrt{3}+2)(4\sqrt{3}+2)}{(4\sqrt{3}-2)(4\sqrt{3}+2)} \\[4pt]
&=\dfrac{16+10\sqrt{3}}{44} \\[4pt]
&=\dfrac{8+5\sqrt{3}}{22}
\end{align*}
弦のなす角に関する問題
2018年 津田塾大$a,~b$ を $0<a<b$ を満たす定数とする。2定点A$(0,~a)$,B$(0,~b)$ と,$x$ 軸上を動く点P$(t,~0)$ を考える。ただし,$t>0$ とする。
(1) 3点A,B,Pを通る円 $C$ の中心の座標を $t,~a,~b$ を用いて表せ。
(2) $\tan\kaku{BPA}$ を $t,~a,~b$ を用いて表せ。
(3) 円 $C$ が $x$ 軸と接するときの $t$ を $a,~b$ を用いて表せ。
(4) $\kaku{BPA}$ の大きさを最大にする $t$ を $a,~b$ を用いて表せ。
(1) 3点A,B,Pを通る円 $C$ の中心の座標を $t,~a,~b$ を用いて表せ。
(2) $\tan\kaku{BPA}$ を $t,~a,~b$ を用いて表せ。
(3) 円 $C$ が $x$ 軸と接するときの $t$ を $a,~b$ を用いて表せ。
(4) $\kaku{BPA}$ の大きさを最大にする $t$ を $a,~b$ を用いて表せ。
【(1)の考え方と解答】
2定点A,Bを通る円は
2定点A,Bを通る円は
\begin{align*}
x^2+(y-a)(y-b)+kx=0~\cdots\cdots(*)
\end{align*}
と表せる。これが点P$(t,~0)$ を通るときx^2+(y-a)(y-b)+kx=0~\cdots\cdots(*)
\end{align*}
\begin{align*}
&t^2+ab+kt=0 \\[4pt]
&k=-t-\dfrac{ab}{t}
\end{align*}
よって,3点A,B,Pを通る円 $C$ の方程式は&t^2+ab+kt=0 \\[4pt]
&k=-t-\dfrac{ab}{t}
\end{align*}
\begin{align*}
&x^2+(y-a)(y-b)-\left(t+\dfrac{ab}{t}\right)x=0 \\[4pt]
&\left\{x-\dfrac{1}{2}\left(t+\dfrac{ab}{t}\right)\right\}^2+\left(y-\dfrac{a+b}{2}\right)^2=\dfrac{1}{4}\left(t+\dfrac{ab}{t}\right)^2+\dfrac{1}{4}(a+b)^2-ab \\[4pt]
&\left\{x-\dfrac{1}{2}\left(t+\dfrac{ab}{t}\right)\right\}^2+\left(y-\dfrac{a+b}{2}\right)^2=\dfrac{1}{4}\left(a^2+b^2+t^2+\dfrac{a^2b^2}{t^2}\right)
\end{align*}
よって,求める円 $C$ の中心の座標は&x^2+(y-a)(y-b)-\left(t+\dfrac{ab}{t}\right)x=0 \\[4pt]
&\left\{x-\dfrac{1}{2}\left(t+\dfrac{ab}{t}\right)\right\}^2+\left(y-\dfrac{a+b}{2}\right)^2=\dfrac{1}{4}\left(t+\dfrac{ab}{t}\right)^2+\dfrac{1}{4}(a+b)^2-ab \\[4pt]
&\left\{x-\dfrac{1}{2}\left(t+\dfrac{ab}{t}\right)\right\}^2+\left(y-\dfrac{a+b}{2}\right)^2=\dfrac{1}{4}\left(a^2+b^2+t^2+\dfrac{a^2b^2}{t^2}\right)
\end{align*}
\begin{align*}
\left(\dfrac{1}{2}\left(t+\dfrac{ab}{t}\right),~\dfrac{a+b}{2}\right)
\end{align*}
\left(\dfrac{1}{2}\left(t+\dfrac{ab}{t}\right),~\dfrac{a+b}{2}\right)
\end{align*}

ヒロ
(*)と表せる理由が分からない人は,次の記事を読むと理解できるだろう。
(2) $\tan\kaku{BPA}$ を $t,~a,~b$ を用いて表せ。
【(2)の考え方と解答】
2直線AP,BPと $x$ 軸の正の方向とのなす角をそれぞれ $\alpha,~\beta$ とすると,
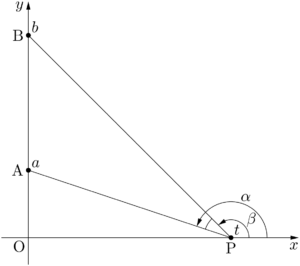
$\kaku{BPA}=\beta-\alpha$ であるから
2直線AP,BPと $x$ 軸の正の方向とのなす角をそれぞれ $\alpha,~\beta$ とすると,
\begin{align*}
\tan\alpha=-\dfrac{a}{t},~\tan\beta=-\dfrac{b}{t}
\end{align*}
となる。\tan\alpha=-\dfrac{a}{t},~\tan\beta=-\dfrac{b}{t}
\end{align*}

$\kaku{BPA}=\beta-\alpha$ であるから
\begin{align*}
\tan\kaku{BPA}&=\tan(\alpha-\beta) \\[4pt]
&=\dfrac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta} \\[4pt]
&=\dfrac{-\dfrac{a}{t}+\dfrac{b}{t}}{1+\left(-\dfrac{a}{t}\right)\Cdota\left(-\dfrac{b}{t}\right)} \\[4pt]
&=\dfrac{b-a}{t+\dfrac{ab}{t}}
\end{align*}
\tan\kaku{BPA}&=\tan(\alpha-\beta) \\[4pt]
&=\dfrac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta} \\[4pt]
&=\dfrac{-\dfrac{a}{t}+\dfrac{b}{t}}{1+\left(-\dfrac{a}{t}\right)\Cdota\left(-\dfrac{b}{t}\right)} \\[4pt]
&=\dfrac{b-a}{t+\dfrac{ab}{t}}
\end{align*}
(3) 円 $C$ が $x$ 軸と接するときの $t$ を $a,~b$ を用いて表せ。
【(3)の考え方と解答】
円 $C$ の $y$ 座標は正であるから,$C$ が $x$ 軸と接するときは,$C$ の中心の $y$ 座標と半径が等しいときである。(1)の結果より
円 $C$ の $y$ 座標は正であるから,$C$ が $x$ 軸と接するときは,$C$ の中心の $y$ 座標と半径が等しいときである。(1)の結果より
\begin{align*}
&\dfrac{a+b}{2}=\dfrac{1}{2}\sqrt{a^2+b^2+t^2+\dfrac{a^2b^2}{t^2}}
\end{align*}
両辺2乗して&\dfrac{a+b}{2}=\dfrac{1}{2}\sqrt{a^2+b^2+t^2+\dfrac{a^2b^2}{t^2}}
\end{align*}
\begin{align*}
&(a+b)^2=a^2+b^2+t^2+\dfrac{a^2b^2}{t^2} \\[4pt]
&t^2-2ab+\dfrac{a^2b^2}{t^2}=0 \\[4pt]
&\left(t-\dfrac{ab}{t}\right)^2=0 \\[4pt]
&t-\dfrac{ab}{t}=0 \\[4pt]
&t^2=ab
\end{align*}
$t>0$ より,$t=\sqrt{ab}$&(a+b)^2=a^2+b^2+t^2+\dfrac{a^2b^2}{t^2} \\[4pt]
&t^2-2ab+\dfrac{a^2b^2}{t^2}=0 \\[4pt]
&\left(t-\dfrac{ab}{t}\right)^2=0 \\[4pt]
&t-\dfrac{ab}{t}=0 \\[4pt]
&t^2=ab
\end{align*}
(4) $\kaku{BPA}$ の大きさを最大にする $t$ を $a,~b$ を用いて表せ。
【(4)の考え方と解答】
$0<\kaku{BPA}<\dfrac{\pi}{2}$ であるから,$\kaku{BPA}$ の大きさが最大になるのは,$\tan\kaku{BPA}$ が最大になるときである。したがって,(2)の結果より,$t+\dfrac{ab}{t}$ が最小になるときであると分かる。
$t>0,~ab>0$ であるから,相加・相乗平均の関係より
よって,$\kaku{BPA}$ の大きさを最大にする $t$ は,$t=\sqrt{ab}$ である。
$0<\kaku{BPA}<\dfrac{\pi}{2}$ であるから,$\kaku{BPA}$ の大きさが最大になるのは,$\tan\kaku{BPA}$ が最大になるときである。したがって,(2)の結果より,$t+\dfrac{ab}{t}$ が最小になるときであると分かる。
$t>0,~ab>0$ であるから,相加・相乗平均の関係より
\begin{align*}
t+\dfrac{ab}{t}\geqq2\sqrt{t\Cdota\dfrac{ab}{t}}=2\sqrt{ab}
\end{align*}
が成り立つ。等号が成り立つのは,$t=\dfrac{ab}{t}$ すなわち $t=\sqrt{ab}$ のときである。t+\dfrac{ab}{t}\geqq2\sqrt{t\Cdota\dfrac{ab}{t}}=2\sqrt{ab}
\end{align*}
よって,$\kaku{BPA}$ の大きさを最大にする $t$ は,$t=\sqrt{ab}$ である。



















