定積分を含む不等式の証明に関する問題演習として,2010年の東京大学で行われた入試問題を扱います。これまで記事で書いてきた考え方を使うことで,解けるようになっていることを期待します。
2010年 東京大学 第二問の考え方

定積分を含む不等式の証明の考え方には,図形の面積の大小関係を考える方法や数式をうまく変形する方法などがあるが,フル活用して次の問題を解いてみよう。
\dfrac{1}{2(k+1)}<\dint{0}{1}\dfrac{1-x}{k+x}\;dx<\dfrac{1}{2k}
\end{align*}
\dfrac{m-n}{2(m+1)(n+1)}<\log\dfrac mn-\Sum{k=n+1}{m}\dfrac1k<\dfrac{m-n}{2mn}
\end{align*}
(1)の考え方

(1)は積分範囲が0から1の定積分で表すことを考えよう。

そんなこと言われても困ります。ヒント下さい!

被積分関数の分母に $x$ が残ると,積分したときに $\log\abs{x}$ が現れてしまって,$x=0$ では定義されないからうまくいかないよね?

ということは,分母には $x$ が残らないようにしないといけないってことですね。

そういうことになるね。でもそれだけ聞いて「なるほど!じゃあこういうことだな!」とサクサク進められる人は少ない。式だけで考えるのが難しいなら,グラフも活用しよう。

じゃあ,まずは定積分で表された式がどんな図形の面積かを考えてみます。
f(x)=\dfrac{1+k}{k+x}-1
\end{align*}
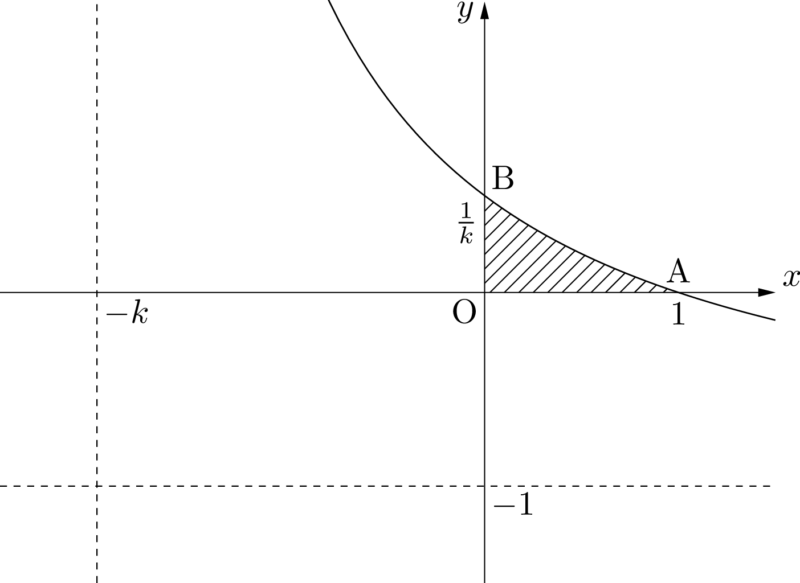

分数式の変形は大丈夫みたいだけど,軽くポイントを押さえておくよ。
$f(x)$ を $g(x)$ で割ったときの商を $Q(x)$,余りを $r(x)$ とすると,
f(x)=g(x)Q(x)+r(x)
\end{align*}
\dfrac{f(x)}{g(x)}=Q(x)+\dfrac{r(x)}{g(x)}
\end{align*}
ここで,$g(x)$ が1次式,例えば $ax+b$ であるとすると,余りは定数となり,それを $R$ とすると,剰余の定理より
R=f\left(-\dfrac{b}{a}\right)
\end{align*}
\dfrac{ax+b}{cx+d}=\dfrac{-\dfrac{ad}{c}+b}{cx+d}+\dfrac{a}{c}
\end{align*}

全然軽くなくて,ガッツリ説明してますね・・・

では話を戻して,続きを考えよう。いまは斜線部分より面積が大きい図形と小さい図形を考えないといけないんだね。

そうですね!

まずは斜線部分より面積が大きい図形を考えようか。

こんな感じですか?
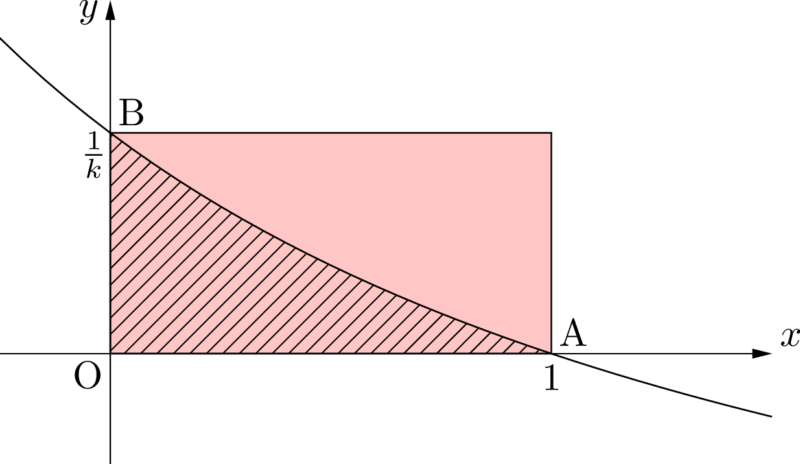

それは長方形?

はい!ダメですか?

確かに大きいんだけど,大きすぎないか?面積計算してみて?

$1\times\dfrac{1}{k}=\dfrac{1}{k}$ ですね。

最右辺は $\dfrac{1}{2k}$ だよ?よく考えてみよう!

あっ!そうか。不等式のこと全く考えてませんでした。半分にすれば良いから,AとBを結んで $\sankaku{OAB}$ にすれば良かったんですね。
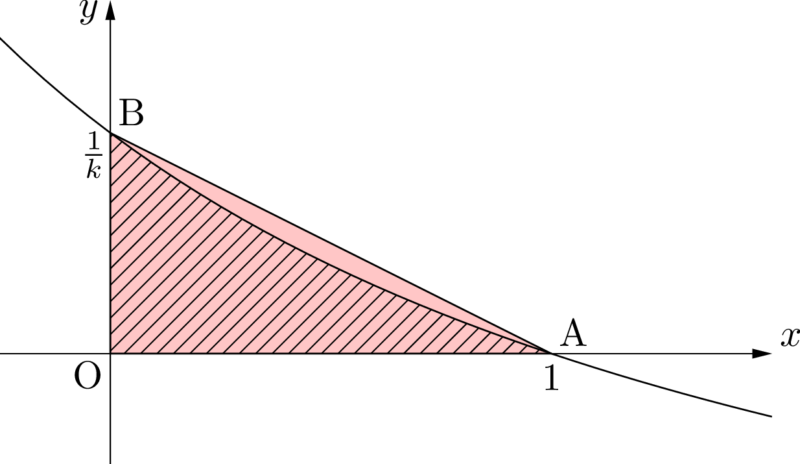

そうだね。なるべく少しだけ面積が異なる図形になるようにした方が良いよ。

はい,分かりました。

では,次は面積が小さい図形を考えよう。

こんな感じですか?
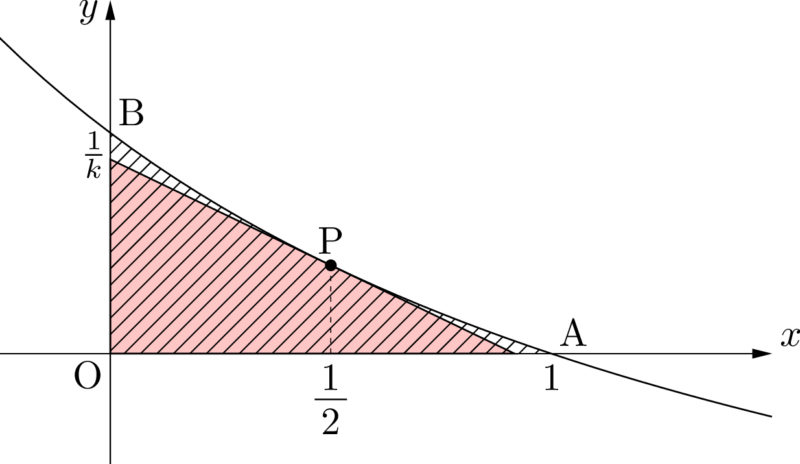

それってどんな直線?

点Pで接する直線です。

ちょうど真ん中の $\dfrac{1}{2}$ の点を選んだ理由は?

う~ん・・・なんとなくです。

その三角形の面積が $\dfrac{1}{2(k+1)}$ なら問題ないけど,そうなってるかな?

分からないけど,そうならない気がします・・・

面積が $\dfrac{1}{2(k+1)}$ になれば良いんだから,こういうのはどうですか?
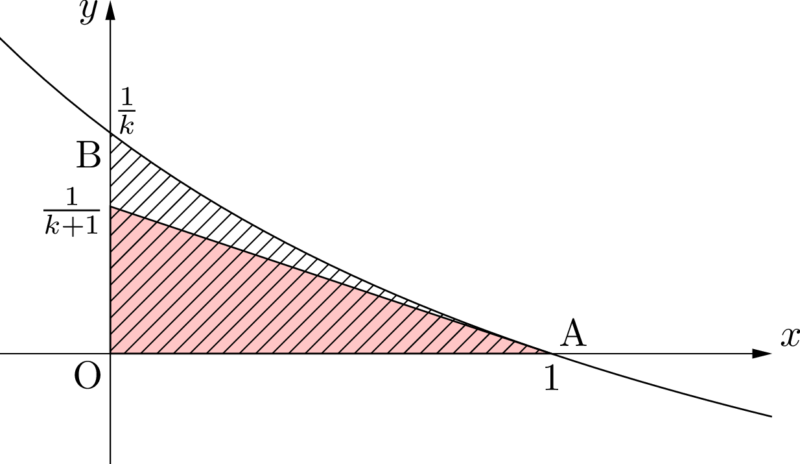

確かにそれなら面積は $\dfrac{1}{2(k+1)}$ になるけど,別の問題が発生するね。

どういうことですか?

まず,正確な情報がないまま,自分の都合の良いように図を描いてしまっている。「点Aの付近で接線が $y=f(x)$ のグラフより上側になることはないか?」ということを気にしないといけないよ。
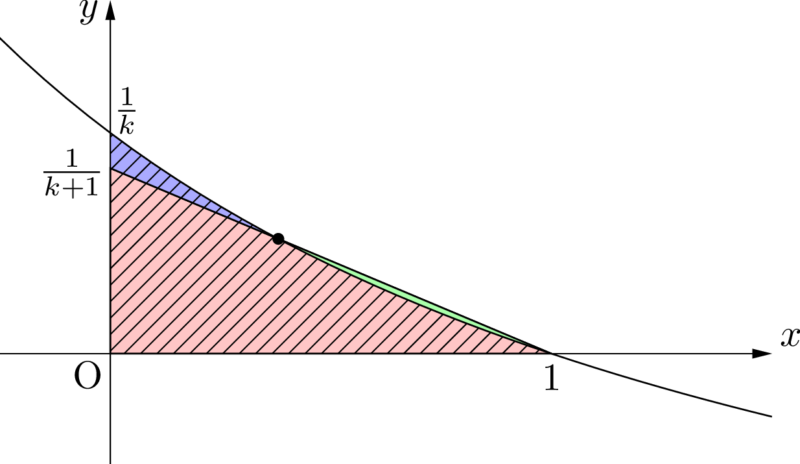

もし,緑色の部分が青色の部分より大きい場合は斜線部分の面積(赤色 $+$ 青色)より,考えた三角形の面積(赤色 $+$ 緑色)の方が大きくなってしまう。

でもグラフを見れば,青色の部分の方が大きいから大丈夫なんじゃないですか?

いや・・・それは都合が良いようにグラフを描いているからそう見えているだけで,実際もそうなっているかは,ちゃんと確認しないと分からないよね?

なるほど・・・確かに都合良く描いてしまっている気がします。

何が言いたいかと言うと,事実と異なる場合があるから,適当に描いたグラフを信じすぎるなということ。あとは細かい部分については,他に共有点があるのかないのかを気にしよう。

じゃあ今回の場合はどうすれば良いんですか?

点Aにおける接線なら,$y=f(x)$ のグラフが下に凸だから $0<x<1$ の範囲では他に共有点はないから都合が良い。あとは切片が $\dfrac{1}{k+1}$ なら全く文句がない状態。実際に確かめてみよう。
f'(x)=-\dfrac{1+k}{(k+x)^2}
\end{align*}
f'(1)=-\dfrac{1+k}{(k+1)^2}=-\dfrac{1}{k+1}
\end{align*}
&y=-\dfrac{1}{k+1}(x-1) \\[4pt]
&y=-\dfrac{x}{k+1}+\dfrac{1}{k+1}
\end{align*}

切片が $\dfrac{1}{k+1}$ だから完璧ですね!

それでは考えを整理しよう。
&y=-\dfrac{1}{k}x+\dfrac{1}{k} \\[4pt]
&y=\dfrac{1-x}{k}
\end{align*}
&y=-\dfrac{x}{k+1}+\dfrac{1}{k+1} \\[4pt]
&y=\dfrac{1-x}{k+1}
\end{align*}
\dint{0}{1}\dfrac{1-x}{k+1}\;dx<\dint{0}{1}\dfrac{1-x}{k+x}\;dx<\dint{0}{1}\dfrac{1-x}{k}\;dx
\end{align*}
\dfrac{1-x}{k+1}\leqq\dfrac{1-x}{k+x}\leqq\dfrac{1-x}{k}
\end{align*}
\dfrac{1}{k+1}\leqq\dfrac{1}{k+x}\leqq\dfrac{1}{k}
\end{align*}
k\leqq k+x\leqq k+1
\end{align*}

なるほど・・・ここまで来たら,その不等式が成り立つことは分かるから,証明としては逆に書いていけば良いってことですね!

そういうこと。では答案を仕上げよう。
(1)の解答
$0\leqq x\leqq1$ のとき,$k\leqq k+x\leqq 1+k$ であるから
\dfrac{1}{k+1}\leqq\dfrac{1}{k+x}\leqq\dfrac{1}{k}
\end{align*}
\dfrac{1-x}{k+1}\leqq\dfrac{1-x}{k+x}\leqq\dfrac{1-x}{k}
\end{align*}
\dint{0}{1}\dfrac{1-x}{k+1}\;dx<\dint{0}{1}\dfrac{1-x}{k+x}\;dx<\dint{0}{1}\dfrac{1-x}{k}\;dx
\end{align*}
\dint{0}{1}\dfrac{1-x}{k+1}\;dx&=\Tint{-\dfrac{(1-x)^2}{2(k+1)}}{0}{1} \\[4pt]
&=\dfrac{1}{2(k+1)} \\[4pt]
\dint{0}{1}\dfrac{1-x}{k}\;dx&=\Tint{-\dfrac{(1-x)^2}{2k}}{0}{1} \\[4pt]
&=\dfrac{1}{2k}
\end{align*}
\dfrac{1}{2(k+1)}<\dint{0}{1}\dfrac{1-x}{k+x}\;dx<\dfrac{1}{2k}
\end{align*}
(2)の考え方

それでは(2)を考えよう。気になる部分はどこ?

最左辺と最右辺が同じような式になってますね。

そうだね。最右辺の $m,~n$ をそれぞれ $m+1,~n+1$ にしたものが最左辺になってるね。

あとは中央の $\log$ が気になります。

入試問題だから,(1)を利用するのだろうなと予想しよう。そうすると,中央の定積分を行うと $\log$ が出てくるのは分かるから,実際にどうなるか確かめるために定積分の計算をしてみよう。
\dint{0}{1}\dfrac{1-x}{k+x}\;dx&=\dint{0}{1}\left(\dfrac{1+k}{k+x}-1\right)\;dx \\[4pt]
&=\Tint{(1+k)\log\abs{k+x}-x}{0}{1} \\[4pt]
&=(1+k)\{\log(k+1)-\log k\}-1
\end{align*}

さて,ここで考えるヒントが $\Sum{k=n+1}{m}\dfrac{1}{k}$ にある。$\Sigma$ を含む不等式の証明では,$\Sigma$ を用いて表すのが基本だったね。

ということは $\log\dfrac{m}{n}$ も $\Sum{k=n+1}{m}$ で表すということですか?

そういうことになるね。定積分をした結果と見比べて考えよう。$\log\dfrac{m}{n}=\log m-\log n$ と表せるのがヒント。

ちょっとやってみます。
\log\dfrac{m}{n}=\Sum{k=n+1}{m}\{\log k-\log(k-1)\}
\end{align*}

でも(1)の不等式と $k$ が1ずれているのと,前に $k+1$ が掛かってます。

そうだね。$k$ のずれは調整すれば良いね。
\Sum{k=n+1}{m}\{\log k-\log(k-1)\}=\Sum{k=n}{m-1}\{\log(k+1)-\log k\}
\end{align*}

でも,前に掛かっている $k+1$ があると,いまやってもらったシグマ計算も意味がなくなるから,処理方法を考えないといけない。つまり $k+1$ をなくせば良いね。

なくせば良いって言われても・・・そのままはなくせないから,どうしたらなくせるかってことを考えろってことですね。

う~ん・・・・じゃあ,もう,これしかないですね。$k+1$ で割る!

いいね!
\dfrac{1}{2(k+1)}<(1+k)\{\log(k+1)-\log k\}-1<\dfrac{1}{2k}
\end{align*}
\dfrac{1}{2(k+1)^2}<\log(k+1)-\log k-\dfrac{1}{k+1}<\dfrac{1}{2k(k+1)}
\end{align*}

$k+1$ が邪魔だから割ったけど,それによって,他の部分もうまくいく形になったね。

じゃあ,この不等式で $k=n,~n+1,~\cdots,~m-1$ として辺々を加えれば証明できるってことですか?

残念ながら,そんなに甘くない。最左辺に着目しよう。部分分数分解して差を作れる最右辺とは違って,最左辺のシグマ計算はできない形なんだ。

でも,とりあえず右側の不等式については,なんとなく証明できそうだから,計算してみよう。
&\Sum{k=n}{m-1}\left\{\log(k+1)-\log k-\dfrac{1}{k+1}\right\}<\Sum{k=n}{m-1}\dfrac{1}{2k(k+1)} \\[4pt]
&\log\dfrac{m}{n}-\Sum{k=n}{m-1}\dfrac{1}{k+1}<\Sum{k=n}{m-1}\dfrac{1}{2}\left(\dfrac{1}{k}-\dfrac{1}{k+1}\right) \\[4pt]
&\log\dfrac{m}{n}-\Sum{k=n+1}{m}\dfrac{1}{k}<\dfrac{1}{2}\left(\dfrac{1}{n}-\dfrac{1}{m}\right) \\[4pt]
&\log\dfrac{m}{n}-\Sum{k=n+1}{m}\dfrac{1}{k}<\dfrac{m-n}{2mn}
\end{align*}

右側の不等式が出てきました!あとは左側ですね・・・

まずは,最左辺を $\Sigma$ を使って表してみよう。
\dfrac{m-n}{2(m+1)(n+1)}=\Sum{k=n}{m-1}\dfrac{1}{2(k+1)(k+2)}
\end{align*}

いまやっているのは不等式の証明だから,大小関係が成り立つことを示すことができれば良いんだよ。

前にも言ったけど,$A>B$ を示したいけど,$A>C$ が成り立つことが分かったのなら,追加で $C>B$ が成り立つことを示せば,$A>B$ が成り立つことを証明できるよね。

ということは,$\dfrac{1}{2(k+1)(k+2)}<\dfrac{1}{2(k+1)^2}$ を証明すれば良いってことですね!でもこれは証明するというか当たり前に成り立ちますね。

そうだね。これで(2)もできるね。
(2)の解答
\dint{0}{1}\dfrac{1-x}{k+x}\;dx&=\dint{0}{1}\left(\dfrac{1+k}{k+x}-1\right)\;dx \\[4pt]
&=\Tint{(1+k)\log\abs{k+x}-x}{0}{1} \\[4pt]
&=(1+k)\{\log(k+1)-\log k\}-1
\end{align*}
&\dfrac{1}{2(k+1)}<(1+k)\{\log(k+1)-\log k\}-1<\dfrac{1}{2k} \\[4pt]
&\dfrac{1}{2(k+1)^2}<\log(k+1)-\log k-\dfrac{1}{k+1}<\dfrac{1}{2k(k+1)}
\end{align*}
\dfrac{1}{2(k+1)(k+2)}<\log(k+1)-\log k-\dfrac{1}{k+1}<\dfrac{1}{2k(k+1)}
\end{align*}
&\Sum{k=n}{m-1}\dfrac{1}{2(k+1)(k+2)}<\Sum{k=n}{m-1}\left\{\log(k+1)-\log k-\dfrac{1}{k+1}\right\}<\Sum{k=n}{m-1}\dfrac{1}{2k(k+1)} \\[4pt]
&\Sum{k=n}{m-1}\dfrac{1}{2}\left(\dfrac{1}{k+1}-\dfrac{1}{k+2}\right) <\log\dfrac{m}{n}-\Sum{k=n}{m-1}\dfrac{1}{k+1}<\Sum{k=n}{m-1}\dfrac{1}{2}\left(\dfrac{1}{k}-\dfrac{1}{k+1}\right) \\[4pt]
&\dfrac{1}{2}\left(\dfrac{1}{n+1}-\dfrac{1}{m+1}\right)<\log\dfrac{m}{n}-\Sum{k=n+1}{m}\dfrac{1}{k}<\dfrac{1}{2}\left(\dfrac{1}{n}-\dfrac{1}{m}\right) \\[4pt]
&\dfrac{m-n}{2(m+1)(n+1)}<\log\dfrac{m}{n}-\Sum{k=n+1}{m}\dfrac{1}{k}<\dfrac{m-n}{2mn}
\end{align*}
調和数列の和の近似

part3の記事でも書いたように,調和数列の和は発散するのだが,この問題を通して,調和数列の和の評価式が得られたことになる。
\dfrac{m-n}{2(m+1)(n+1)}<\log\dfrac{m}{n}-\Sum{k=n+1}{m}\dfrac{1}{k}<\dfrac{m-n}{2mn}
\end{align*}
&\dfrac{m-1}{4(m+1)}<\log m-\Sum{k=2}{m}\dfrac{1}{k}<\dfrac{m-1}{2m} \\[4pt]
&\log m-\dfrac{m-1}{2m}<\Sum{k=2}{m}\dfrac{1}{k}<\log m-\dfrac{m-1}{4(m+1)} \\[4pt]
&1+\log m-\dfrac{m-1}{2m}<\Sum{k=1}{m}\dfrac{1}{k}<1+\log m-\dfrac{m-1}{4(m+1)}
\end{align*}
1+\log m-\dfrac{m-1}{2m}\leqq\Sum{k=1}{m}\dfrac{1}{k}\leqq1+\log m-\dfrac{m-1}{4(m+1)}
\end{align*}

これで調和数列の和の近似値が知りたくなったら,自然対数表を見ればすぐに出せるね!

そんな日は来ない気がしますけどね・・・
まとめ

定積分や和の記号 $\Sigma$ を含む不等式の証明において,式変形による解法だけでは難しい場合は図形の面積の大小関係に着目して問題を解く手助けにしよう。

また,証明すべきゴールの不等式から何を証明すれば良いかを考えることは非常に有効な方法なので覚えておこう。























