ここでは2016年センター試験 数学ⅡB 第1問三角関数の解説をします。
まだ問題を解いていない人は解いてから解説を読んでください。
2016年 センターⅡB 三角関数$k$ を正の定数として
(1) $0<x<\dfrac{\pi}{2}$ の範囲で①を満たす $x$ の個数について考えよう。
①の両辺に $\sin^2x\cos^2x$ をかけ,2倍角の公式を用いて変形すると
(2) $k=\dfrac{4}{25}$ とし,$\dfrac{\pi}{4}<x<\dfrac{\pi}{2}$ の範囲で①を満たす $x$ について考えよう。
②により $\sin2x=\dfrac{\myBox{ヌ}}{\myBox{ネ}}$ であるから
\begin{align*}
\cos^2x-\sin^2x+k\left(\dfrac{1}{\cos^2x}-\dfrac{1}{\sin^2x}\right)=0 ~\cdots\cdots①
\end{align*}
を満たす $x$ について考える。\cos^2x-\sin^2x+k\left(\dfrac{1}{\cos^2x}-\dfrac{1}{\sin^2x}\right)=0 ~\cdots\cdots①
\end{align*}
(1) $0<x<\dfrac{\pi}{2}$ の範囲で①を満たす $x$ の個数について考えよう。
①の両辺に $\sin^2x\cos^2x$ をかけ,2倍角の公式を用いて変形すると
\begin{align*}
\left(\dfrac{\sin^22x}{\myBox{チ}}-k\right)\cos2x=0 ~\cdots\cdots②
\end{align*}
を得る。したがって,$k$ の値に関係なく,$x=\dfrac{\pi}{\myBox{ツ}}$ のときはつねに①が成り立つ。また,$0<x<\dfrac{\pi}{2}$ の範囲で $0<\sin^22x\leqq1$ であるから,$k>\dfrac{\myBox{テ}}{\myBox{ト}}$ のとき,①を満たす $x$ は $\dfrac{\pi}{\mybox{ツ}}$ のみである。一方,$0<k<\dfrac{\mybox{テ}}{\mybox{ト}}$ のとき,①を満たす $x$ の個数は $\myBox{ナ}$ 個であり,$k=\dfrac{\mybox{テ}}{\mybox{ト}}$ のときは $\myBox{ニ}$ 個である。\left(\dfrac{\sin^22x}{\myBox{チ}}-k\right)\cos2x=0 ~\cdots\cdots②
\end{align*}
(2) $k=\dfrac{4}{25}$ とし,$\dfrac{\pi}{4}<x<\dfrac{\pi}{2}$ の範囲で①を満たす $x$ について考えよう。
②により $\sin2x=\dfrac{\myBox{ヌ}}{\myBox{ネ}}$ であるから
\begin{align*}
\cos2x=\dfrac{\myBox{ノハ}}{\myBox{ヒ}}
\end{align*}
である。したがって\cos2x=\dfrac{\myBox{ノハ}}{\myBox{ヒ}}
\end{align*}
\begin{align*}
\cos x=\dfrac{\sqrt{\myBox{フ}}}{\myBox{ヘ}}
\end{align*}
である。\cos x=\dfrac{\sqrt{\myBox{フ}}}{\myBox{ヘ}}
\end{align*}
(1)の解答

ヒロ
誘導通りに変形していこう。
【チの解答】
①の両辺に $\sin^2x\cos^2x$ をかけると
①の両辺に $\sin^2x\cos^2x$ をかけると
\begin{align*}
&\sin^2x\cos^2x(\cos^2x-\sin^2x)+k(\sin^2x-\cos^2x)=0 \\[4pt]
&(\sin^2x\cos^2x-k)(\cos^2x-\sin^2x)=0 \\[4pt]
&\left(\dfrac{\sin^22x}{4}-k\right)\cos2x=0
\end{align*}
&\sin^2x\cos^2x(\cos^2x-\sin^2x)+k(\sin^2x-\cos^2x)=0 \\[4pt]
&(\sin^2x\cos^2x-k)(\cos^2x-\sin^2x)=0 \\[4pt]
&\left(\dfrac{\sin^22x}{4}-k\right)\cos2x=0
\end{align*}

ヒロ
$k$ の値に関係ない①の解を求めよう。
【ツの解答】
$k$ の値に関係なく①が成り立つのは
$k$ の値に関係なく①が成り立つのは
\begin{align*}
\cos2x=0
\end{align*}
となるときである。$0<2x<\pi$ より\cos2x=0
\end{align*}
\begin{align*}
&2x=\dfrac{\pi}{2} \\[4pt]
&x=\dfrac{\pi}{4}
\end{align*}
&2x=\dfrac{\pi}{2} \\[4pt]
&x=\dfrac{\pi}{4}
\end{align*}

ヒロ
次の $\myBox{テ}$ と $\myBox{ト}$ はちゃんと意味を考えよう。
【テ~ナの解答】
①を満たす $x$ が $\dfrac{\pi}{4}$ のみになるのは,
ここで,$0<x<\dfrac{\pi}{2}$ のとき,$0<\sin^22x\leqq1$ より,
よって,$k>\dfrac{1}{4}$ のとき,①を満たす $x$ は $\dfrac{\pi}{4}$ のみである。
①を満たす $x$ が $\dfrac{\pi}{4}$ のみになるのは,
\begin{align*}
\dfrac{\sin^22x}{4}-k=0
\end{align*}
が解をもたないときである。\dfrac{\sin^22x}{4}-k=0
\end{align*}
ここで,$0<x<\dfrac{\pi}{2}$ のとき,$0<\sin^22x\leqq1$ より,
\begin{align*}
&-k<\dfrac{\sin^22x}{4}-k\leqq\dfrac{1}{4}-k
\end{align*}
となる。$k>0$ であることを考えると,&-k<\dfrac{\sin^22x}{4}-k\leqq\dfrac{1}{4}-k
\end{align*}
\begin{align*}
\dfrac{1}{4}-k<0
\end{align*}
となるとき,$\dfrac{\sin^22x}{4}-k=0$ は解をもたない。\dfrac{1}{4}-k<0
\end{align*}
よって,$k>\dfrac{1}{4}$ のとき,①を満たす $x$ は $\dfrac{\pi}{4}$ のみである。

ヒロ
次は解の個数を求める問題。
【ナニの解答】
$0<k<\dfrac{1}{4}$ のとき,$\dfrac{\sin^22x}{4}-k$ は負の値 $-k$ から,正の値 $\dfrac{1}{4}-k$ まで取り得るから
2個とも $\dfrac{\pi}{4}$ と異なるから,$x=\dfrac{\pi}{4}$ と合わせて,①を満たす $x$ の個数は3個である。
$0<k<\dfrac{1}{4}$ のとき,$\dfrac{\sin^22x}{4}-k$ は負の値 $-k$ から,正の値 $\dfrac{1}{4}-k$ まで取り得るから
\begin{align*}
\dfrac{\sin^22x}{4}-k=0
\end{align*}
を満たす $x$ が存在する。$0<x<\dfrac{\pi}{2}$ のとき,$0<2x<\pi$ より,$\sin2x>0$ であるから\dfrac{\sin^22x}{4}-k=0
\end{align*}
\begin{align*}
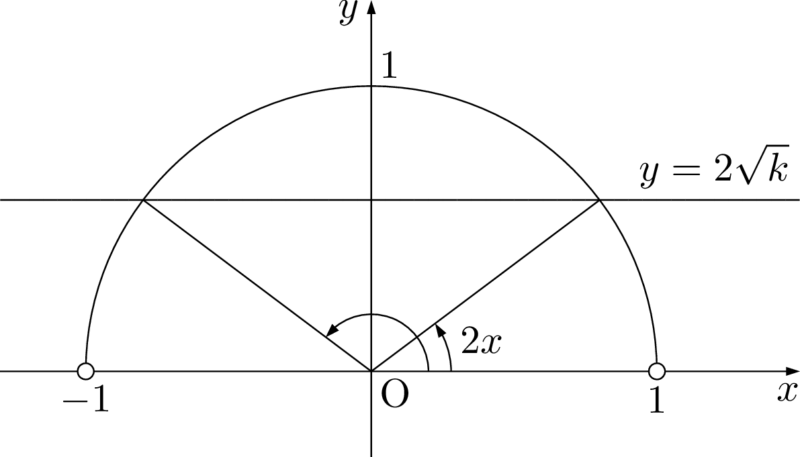
\sin2x=2\sqrt{k}
\end{align*}
よって,これを満たす $2x$ は2個存在する。このうち一方は $0<2x<\dfrac{\pi}{2}$ すなわち $0<x<\dfrac{\pi}{4}$ の部分にある。もう一方は $\dfrac{\pi}{2}<2x<\pi$ すなわち $\dfrac{\pi}{4}<x<\dfrac{\pi}{2}$ の部分にある。\sin2x=2\sqrt{k}
\end{align*}

2個とも $\dfrac{\pi}{4}$ と異なるから,$x=\dfrac{\pi}{4}$ と合わせて,①を満たす $x$ の個数は3個である。

ヒロ
(1)の最後は $k$ の値が定まっているから楽だろう。
【ニの解答】
$k=\dfrac{1}{4}$ のとき,$2\sqrt{k}=1$ であるから,$\dfrac{\sin^22x}{4}-k=0$ を解くと
$k=\dfrac{1}{4}$ のとき,$2\sqrt{k}=1$ であるから,$\dfrac{\sin^22x}{4}-k=0$ を解くと
\begin{align*}
&\sin2x=1 \\[4pt]
&2x=\dfrac{\pi}{2} \\[4pt]
&x=\dfrac{\pi}{4}
\end{align*}
これは $k$ の値と関係ない解 $x=\dfrac{\pi}{4}$ と一致するから,①を満たす $x$ の個数は1個である。&\sin2x=1 \\[4pt]
&2x=\dfrac{\pi}{2} \\[4pt]
&x=\dfrac{\pi}{4}
\end{align*}
(2)の解答
(2) $k=\dfrac{4}{25}$ とし,$\dfrac{\pi}{4}<x<\dfrac{\pi}{2}$ の範囲で①を満たす $x$ について考えよう。
②により $\sin2x=\dfrac{\myBox{ヌ}}{\myBox{ネ}}$ であるから\begin{align*}である。したがって
\cos2x=\dfrac{\myBox{ノハ}}{\myBox{ヒ}}
\end{align*}\begin{align*}である。
\cos x=\dfrac{\sqrt{\myBox{フ}}}{\myBox{ヘ}}
\end{align*}

ヒロ
まずは $k=\dfrac{4}{25}$ を②に代入しよう。
【ヌネの解答】
$k=\dfrac{4}{25}$ のとき,②より
$k=\dfrac{4}{25}$ のとき,②より
\begin{align*}
&\left(\dfrac{\sin^22x}{4}-\dfrac{4}{25}\right)\cos2x=0
\end{align*}
$\dfrac{\pi}{4}<x<\dfrac{\pi}{2}$ のとき,$\cos2x\neq0$ であるから&\left(\dfrac{\sin^22x}{4}-\dfrac{4}{25}\right)\cos2x=0
\end{align*}
\begin{align*}
&\dfrac{\sin^22x}{4}-\dfrac{4}{25}=0 \\[4pt]
&\sin^22x=\dfrac{16}{25}
\end{align*}
$\dfrac{\pi}{2}<2x<\pi$ より,$\sin2x>0$ であるから&\dfrac{\sin^22x}{4}-\dfrac{4}{25}=0 \\[4pt]
&\sin^22x=\dfrac{16}{25}
\end{align*}
\begin{align*}
\sin2x=\dfrac{4}{5}
\end{align*}
\sin2x=\dfrac{4}{5}
\end{align*}

ヒロ
次は $\sin2x$ の値から $\cos2x$ の値を求める問題。直角三角形を描くのがオススメ。
【ノ~ヒの解答】
$\sin2x=\dfrac{4}{5}$ だから,次の直角三角形を描こう。
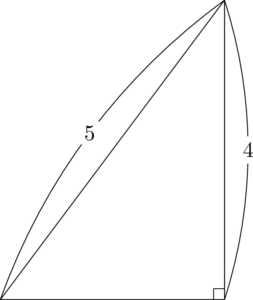
$3:4:5$ の有名直角三角形だと分かるから,底辺の長さは3である。ここで,$\dfrac{\pi}{2}<2x<\pi$ より,$\cos2x<0$ であるから,$\cos2x=\dfrac{-3}{5}$ となる。
$\sin2x=\dfrac{4}{5}$ だから,次の直角三角形を描こう。

$3:4:5$ の有名直角三角形だと分かるから,底辺の長さは3である。ここで,$\dfrac{\pi}{2}<2x<\pi$ より,$\cos2x<0$ であるから,$\cos2x=\dfrac{-3}{5}$ となる。

ヒロ
説明するために図を描いているが,実際には $\sin2x=\dfrac{4}{5}$ を見た瞬間,いま描いた直角三角形が想像できるため,すぐに $\cos2x=-\dfrac{3}{5}$ と分かる。

ヒロ
最後は2倍角の公式を使って $\cos x$ の値を求めよう。
【フヘの解答】
$\cos2x=-\dfrac{3}{5}$ より
$\cos2x=-\dfrac{3}{5}$ より
\begin{align*}
&2\cos^2x-1=-\dfrac{3}{5} \\[4pt]
&\cos^2x=\dfrac{1}{5} \\[4pt]
&\cos x=\pm\dfrac{1}{\sqrt{5}}
\end{align*}
$\dfrac{\pi}{4}<x<\dfrac{\pi}{2}$ より,$\cos x>0$ であるから&2\cos^2x-1=-\dfrac{3}{5} \\[4pt]
&\cos^2x=\dfrac{1}{5} \\[4pt]
&\cos x=\pm\dfrac{1}{\sqrt{5}}
\end{align*}
\begin{align*}
\cos x=\dfrac{\sqrt{5}}{5}
\end{align*}
\cos x=\dfrac{\sqrt{5}}{5}
\end{align*}
2016年 センター数学IIB 三角関数を解いた感想

ヒロ
2016年の三角関数の問題では,2倍角の公式を使いこなせることが重要。

ヒロ
また,三角関数の方程式が解をもつことの意味が分かっていることも重要。

ヒロ
(1)を解くことができる実力がある人にとっては,(2)はボーナス問題になるので,点数差が大きくなるように作られている。

ヒロ
仮に $\myBox{テ}$ ~ $\myBox{ニ}$ が分からなくても,(2)を解くことはできるので,途中で諦めず,次の問題を見るようにするのが良い。




















