図形の性質の考え方・解き方の第三弾です。第一弾・第二弾をご覧になっていない方は,お手数ですが,まずは第一弾からご覧ください。理解がしやすくなるはずです。
センター試験の数学IAの図形問題の考え方を説明します。
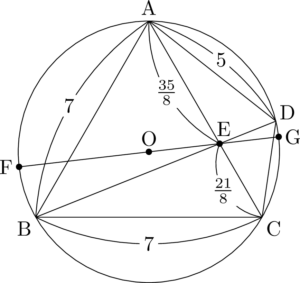
円Oの点Bを含まない弧CA上に,点Dを弦CDの長さが3になるようにとる。このとき,$\kaku{ADC}=\myBox{アイウ}\Deg$ であり,$\mathrm{AD}=\myBox{エ}$ となる。したがって,$\sin\kaku{ACD}=\dfrac{\myBox{オ}\sqrt{\myBox{カ}}}{\myBox{キク}}$ である。
次に,線分ACと線分BDの交点をEとおく。このとき,$\kaku{BDC}=\myBox{ケコ}\Deg$ であり,$\mathrm{AE:EC}=\myBox{サ}:3$ である。したがって,$\mathrm{AE}=\dfrac{\myBox{シス}}{\myBox{セ}}$ である。
この結果を用いて線分OEの長さを求めよう。直線OEと円Oとの二つの交点をF, Gとする。ただし,Eに近い方をG, 遠い方をFとする。このとき,$\mathrm{EF \Cdot EG}=\dfrac{\myBox{ソタチ}}{\myBox{ツテ}}$ となる。よって,$\mathrm{OE}=\dfrac{\myBox{ト}\sqrt{\myBox{ナニ}}}{\myBox{ヌネ}}$である。
Contents
円に内接する正三角形の描き方

まずは図を描こう。三角形ABCは円に内接する正三角形だからキレイに描けるはず。

円を描いてから底辺BCを描きます。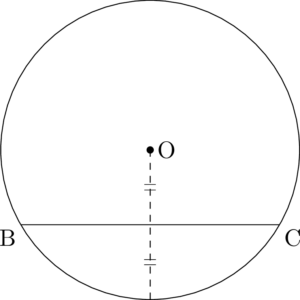

頂点Aを適切な位置にとって正三角形ABCを描きます。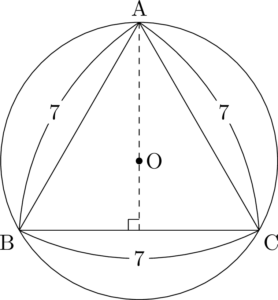

次に点Dを $\mathrm{CD}=3$ となるようにとります。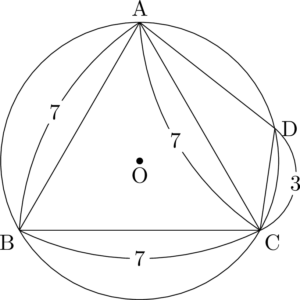

いいね。ここまで描いた時点で分かることを書き込もう。

$B=60\Deg$ だから $D=120\Deg$ と分かります。さらに $\sankaku{ACD}$ が七五三三角形と分かるから $\mathrm{AD}=5$ となります。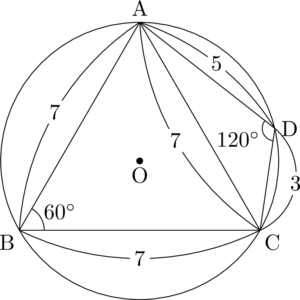

いいね!これでア~エが埋まったね。あと,内接四角形の隣り合う2辺の長さが等しいので,BDが $\kaku{ADC}$ の二等分線になることも頭の片隅に留めておこう。その場合,BDの長さは・・・

BDの長さは8ですね!名古屋三角形と悩み三角形が出てきますね。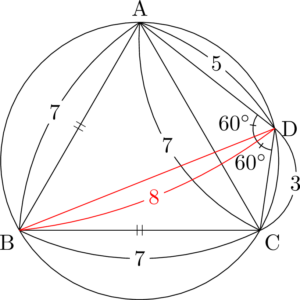

おおっ!カンペキだね。脱線したので戻って,次に進もう。
問題文にある「したがって」などの接続詞に注意しよう

$\sin\kaku{ACD}$ は問題文の「したがって」という接続詞がヒントになってるね。

$\mathrm{AD}=5$ が分かることによって,$\sin\kaku{ACD}$ も求められますよって言われているのだから,それらの関係に着目するのは自然な流れ。$\mathrm{AD}$ と $\kaku{ACD}$ は1組の向かい合う辺と角だから,分かっている向かい合う辺と角をもう1組探そう。

$\mathrm{AC}$ と $\kaku{ADC}$ がありますね。

そうだね。これで正弦定理で $\sin\kaku{ACD}$ を求められる。
&7\sin\kaku{ACD}=5\sin120\Deg \\[4pt]
&\sin\kaku{ACD}=\dfrac{5\sqrt{3}}{14}
\end{align*}
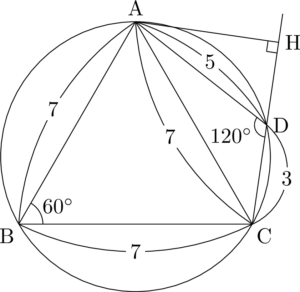

ACとBDの交点がEとあるから,図に書き込もう。

BDが $\kaku{ADC}$ の二等分線になることが最初の方で分かっていたので,楽ですね。$\kaku{BDC}=60\Deg$ で,角の二等分線の性質から $\mathrm{AE:EC}=5:3$ です。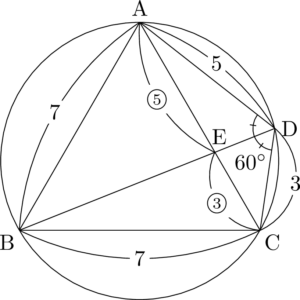
a:b=c:d
\end{align*}
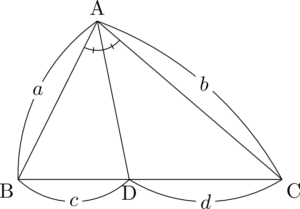

円に内接する四角形で隣り合う辺の長さが等しいときは「角の二等分線の問題を出すだろうな」と思えるようになると,かなり楽になる。

この結果からAEの長さを求めよう。AEの長さはACを8等分したものの5つ分だから簡単に求められる。
\mathrm{AE}=\dfrac{5}{8}\mathrm{AC}=\dfrac{35}{8}
\end{align*}
$\mathrm{AE:EC}=5:3$ より,$\mathrm{AE:AC}=5:8$ だから
&\mathrm{AE}:7=5:8 \\[4pt]
&8\mathrm{AE}=35 \\[4pt]
&\mathrm{AE}=\dfrac{35}{8}
\end{align*}

これでも間違いではないが,速く解くことも目的とするなら間違った解き方である。AEの長さが全体の $\dfrac{5}{8}$ になることがすぐに分からないのは,割合に関する知識がほとんどないのが原因なので,小学5年生で習う「割合」から真面目に復習することを勧める。
方べきの定理とその利用

それでは後半へ進もう。

問題文に合うように2点F, Gをとろう。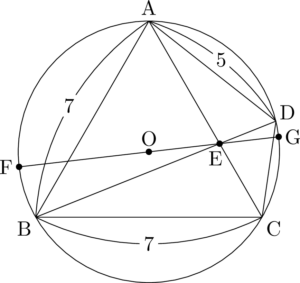
「それぞれの辺の長さを求めて,それを掛ければ良いな」と思ってはいけない。解いているのは大学入試問題である。それぞれの長さが簡単に分かるのなら,別々に出題すれば良いし,それらを求めさせて,さらに掛けた値を求めてね,なんて問題は通常は出ない。
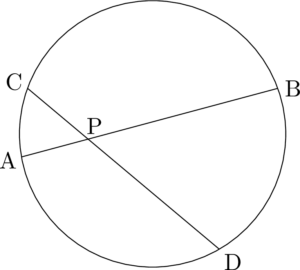
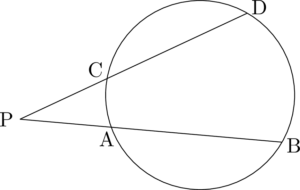
円の2つの弦AB, CDの交点,またはそれらの延長の交点をPとすると次式が成り立つ。
\mathrm{PA\Cdota PB=PC\Cdota PD}
\end{align*}
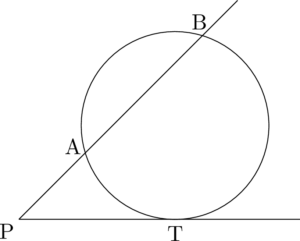
円の外部の点Pから円に引いた接線の接点をTとする。Pを通ってこの円と2点A, Bで交わる直線を引くと次式が成り立つ。
\mathrm{PA\Cdota PB=PT^2}
\end{align*}

方べきの定理をいつ使うのかを覚えておこう。
- 線分の長さの積
- 円の外部の点と円周上の点の間の距離
- 弦またはその一部の長さ

今回は $\mathrm{EF\Cdot EG}$ を求める問題だけど,EFやEGってどうやったら求められるんだろうって考えること自体が間違い。中には変な問題もあるけど,通常は方べきの定理を使って,別の辺の積の問題に置き換える。

EFとEGの積を考えるんだから,点Eを通る弦を探すと,ACとBDがあることが分かる。どちらを使うかは問題文にある「この結果を用いて」で分かる。

ここで言われている「この結果」というのはAEの長さが分かったことなのだから,弦ACを使うことを考えるのは当然。ACの長さは分かっているからECの長さも求められる。
\mathrm{EC}=\dfrac{3}{8}\mathrm{AC}=\dfrac{21}{8}
\end{align*}
方べきの定理より
\mathrm{EF\Cdota EG}&=\mathrm{EA\Cdota EC} \\[4pt]&=\dfrac{35}{8}\Cdota\dfrac{21}{8} \\[4pt]&=\dfrac{735}{64}
\end{align*}
直径を利用する方べきの定理の使い方

最後のOEを求めよう。

ここで「方べきの定理」の使い方として,直径を利用する方法があることを覚えておこう。

問題文の「よって」というのは,当然 $\mathrm{EF\Cdot EG}=\dfrac{735}{64}$ をうけているわけだから,OEとEFやOEとEGの関係を考えないといけない。ここでOFとOGは $\sankaku{ABC}$ の外接円の半径になっていることにも注目しよう。
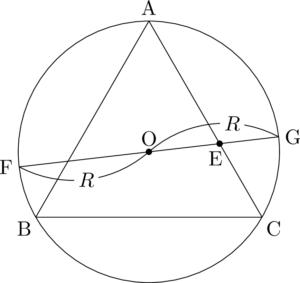
$\sankaku{ABC}$ の外接円の半径を $R$ とすると,
\begin{cases}
\mathrm{EF}=R+\mathrm{OE} \\[4pt]
\mathrm{EG}=R-\mathrm{OE}
\end{cases}
\end{align*}
&(R+\mathrm{OE})(R-\mathrm{OE})=\dfrac{735}{64} \\[4pt]
&R^2-\mathrm{OE}^2=\dfrac{735}{64} \\[4pt]
&\mathrm{OE}^2=R^2-\dfrac{735}{64}
\end{align*}
R=\dfrac{7}{2\sin120\Deg}=\dfrac{7}{\sqrt{3}}
\end{align*}
\mathrm{OE}^2&=\dfrac{7^2}{3}-\dfrac{7^2\Cdot15}{8^2} \\[4pt]
&=\dfrac{7^2(8^2-15))}{3\Cdot8^2} \\[4pt]
&=\dfrac{7^2\Cdot19}{3\Cdot8^2}
\end{align*}
\mathrm{OE}=\dfrac{7\sqrt{19}}{8\sqrt{3}}=\dfrac{7\sqrt{57}}{24}
\end{align*}

上の計算をするときに,$\dfrac{735}{64}$ を $\dfrac{7^2\Cdot15}{8^2}$ と変形してるけど,これは元々 $\dfrac{35}{8}\Cdot\dfrac{21}{8}$ からきていることを利用している。また,そもそもその変形をする理由は二つある。

1つはOEを表す式の分子が $\myBox{ト}\sqrt{\myBox{ナニ}}$ となっていること。もう1つは $R^2$ の分子に $7^2$ が現れること。

なるほど。それで7を根号の外に出せることが分かるから,その変形をするんですね。

そういうこと。$\dfrac{735}{64}$ の分子が $7^2$ を因数にもつことが,すぐに分からないと意味ないけどね。

自分がした計算くらい覚えとけってことですね。

きつく言えばそうなるね。
2006年センター数学IA図形を解いた感想

図形問題で重要なことは,図をできるだけ正確に描くこと。

知っている三角形があれば,それだけで計算しなくても分かる部分がある。また,隣り合う2辺の長さが等しい四角形が円に内接するときは,角の二等分線の存在とそれに関連する問題が待っていると思えるようにしよう。

問題文の接続詞に着目することで因果関係が分かるため,問題を解く糸口をつかみやすくなる。また,複雑な計算も工夫することで簡単になる。























