3次関数とその接線で囲まれた部分の面積を求める公式も12分の1公式と呼ばれています。
他の公式と同様に「12分の1公式は使えない」などと言う人がいますが,そんな声には耳を傾けず,12分の1公式の証明を理解して,その使い方をマスターしましょう。
今回は2019年に立命館大学で出題された入試問題を扱って説明します。
Contents
3次関数とその接線で囲まれる図形の面積を求める入試問題【2019年 立命館大】

まずは $a,~b$ の値を求めよう。
$f(x)=x^3+ax^2+bx$ より
f'(x)=3x^2+2ax+b
\end{align*}
&\begin{cases}
-\dfrac{2a}{3}=-4+2 \\[4pt]
\dfrac{b}{3}=-4\Cdot2
\end{cases} \\[4pt]
&a=3,~b=-24
\end{align*}

次は接線 $l$ の方程式を求めよう。
f(1)=1+3-24=-20,~f'(1)=3+6-24=-15
\end{align*}
&y=-15(x-1)-20 \\[4pt]
&y=-15x-5
\end{align*}

最後の面積を求めよう。
$y=f(x)$ の変曲点の $x$ 座標は $-\dfrac{a}{3}=-1$ で接点の $x$ 座標が1だから,$y=f(x)$ と接線 $l$ の接点以外の共有点の $x$ 座標は
3\Cdota(-1)-2\Cdota1=-5
\end{align*}

よって,$y=f(x)$ のグラフと接線 $l$ で囲まれた部分は下図の斜線部分である。
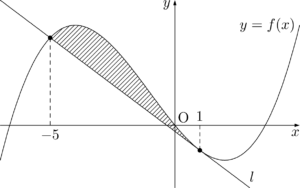
したがって,求める面積を $S$ とすると
S&=\dint{-5}{1}\{(x^3+3x^2-24x)-(-15x-5)\}\;dx \\[4pt]
&=\dint{-5}{1}(x-1)^2(x+5)\;dx \\[4pt]
&=\dint{-5}{1}(x-1)^2(x-1+6)\;dx \\[4pt]
&=\dint{-5}{1}\{(x-1)^3+6(x-1)^2\}\;dx \\[4pt]
&=\Tint{\dfrac{1}{4}(x-1)^4+2(x-1)^3}{-5}{1} \\[4pt]
&=-\dfrac{1}{4}(-6)^4-2(-6)^3 \\[4pt]
&=108
\end{align*}

全部バラバラにして積分するのではなく,カタマリを作って積分しよう。数学IIIを学習している人は部分積分で処理しても良い。
S&=\dint{-5}{1}(x-1)^2(x+5)\;dx \\[4pt]
&=\Tint{\dfrac{1}{3}(x-1)^3(x+5)}{-5}{1}-\dint{-5}{1}\dfrac{1}{3}(x-1)^3\;dx \\[4pt]
&=-\Tint{\dfrac{1}{12}(x-1)^4}{-5}{1} \\[4pt]
&=\dfrac{1}{12}(-6)^4 \\[4pt]
&=108
\end{align*}

また,割り算を利用して $C$ と $l$ の共有点を求めても良い。

余りが出る割り算も暗算で出来るとカンペキだね。
x^3+3x^2-24x=(x-1)^2(x+5)-15x-5
\end{align*}
y=-15x-5
\end{align*}

割り算を行うだけで,接線の方程式ともう1つの共有点の $x$ 座標が求められるのは,このようなマーク式試験において,時間を短縮するのに効果的だね。

この後,面積を求める12分の1公式を忘れていて,積分することになったとしても,被積分関数が $(x-1)^2(x+5)$ となることがすぐに分かる。
3次関数とその接線で囲まれる図形の面積を求める12分の1公式

それでは12分の1公式の証明をしていこう。
f(x)-g(x)=a(x-\alpha)^2(x-\beta)
\end{align*}
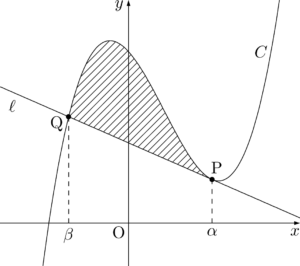
よって,
S&=\dint{\beta}{\alpha}a(x-\alpha)^2(x-\beta)\;dx \\[4pt]
&=\dint{\beta}{\alpha}a(x-\alpha)^2\{(x-\alpha)+(\alpha-\beta)\}\;dx \\[4pt]
&=\dint{\beta}{\alpha}a\{(x-\alpha)^3+(\alpha-\beta)(x-\alpha)^2\}\;dx \\[4pt]
&=a\Tint{\dfrac{1}{4}(x-\alpha)^4+\dfrac{\alpha-\beta}{3}(x-\alpha)^3}{\beta}{\alpha} \\[4pt]
&=a\left\{-\dfrac{1}{4}(\beta-\alpha)^4+\dfrac{1}{3}(\beta-\alpha)^4\right\} \\[4pt]
&=\dfrac{a}{12}(\beta-\alpha)^4
\end{align*}
3次関数 $C:y=f(x)$ 上の点Pにおける接線を $\ell$ とし,$\ell$ が $C$ と再び交わる点をQとする。このとき $\ell$ と $C$ で囲まれた図形の面積を $S$ とすると,
S=\dfrac{\abs{a}}{12}d^4
\end{align*}
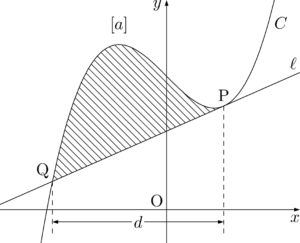
2019年 立命館大の別解

最初に説明した2019年立命館大の別解を解説していこう。

最初に定積分で求めた面積も,12分の1公式を使うことで,面積を次のように求めることができる。

$x^3$ の係数が1で,幅が $d=1-(-5)=6$ であるから
S&=\dfrac{1}{12}\Cdota6^4=108
\end{align*}
3次関数に関する12分の1公式を利用した面積比

3次関数に関する12分の1公式を利用することで簡単に面積を求めることができる。

これによって,もう1つの有名な面積比についても理解して使えるようにしよう。
3次関数 $C:y=f(x)$ 上の点Pにおける接線を $\ell$ とし,$\ell$ が $C$ と再び交わる点をQとする。さらに点Qにおける接線を $m$ とし,$m$ が $C$ と再び交わる点をRとする。このとき $\ell,~m$ と $C$ で囲まれた図形の面積をそれぞれ $S_1,~S_2$ とする。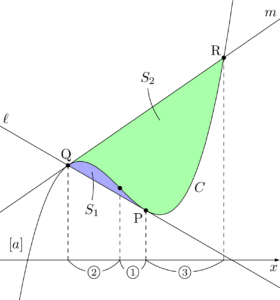
図において,$①=d$ とおくと,
S_1=\dfrac{\abs{a}}{12}(3d)^4,~S_2=\dfrac{\abs{a}}{12}(6d)^4
\end{align*}
&S_1:S_2=3^4:6^4=1:16
\end{align*}
3次関数の12分の1公式に関連する入試問題【2018年 昭和女子大】

もう1問やっておこう。
(1) $f(x)$ は $x=\myBox{アイ}$ で極大値 $\myBox{ウ}$ をとり,$x=\myBox{エ}$ で極小値 $\dfrac{\myBox{オカキ}}{\myBox{ク}}$ をとる。
(2) $C$ 上の点 $\mathrm{A}\left(-1,~\dfrac{7}{2}\right)$ における接線を $l$ とすると,$l$ の方程式は $y=\myBox{ケコ}\,x-\dfrac{\myBox{サ}}{\myBox{シ}}$ である。
曲線 $C$ と直線 $l$ の共有点のうち,Aと異なる点をBとする。このとき,Bの $x$ 座標は $\dfrac{\myBox{ス}}{\myBox{セ}}$ である。したがって,曲線 $C$ と直線 $l$ で囲まれた図形の面積を $S$ とすると,$S=\dfrac{\myBox{ソタ}}{\myBox{チツ}}$ である。
(3) 点 $\mathrm{A}\left(-1,~\dfrac{7}{2}\right)$ から曲線 $C$ に引いた接線のうち,$l$ と異なるものを $m$ とすると,$m$ の方程式は
y=\dfrac{\myBox{テトナニ}}{\myBox{ヌネ}}\,x-\dfrac{\myBox{ノハ}}{\myBox{ヒフ}}
\end{align*}

サクサク求めていこう。
$f(x)=x^3+\dfrac{3}{2}x^2-6x-3$ より
f'(x)&=3x^2+3x-6 \\[4pt]
&=3(x+2)(x-1)
\end{align*}
$x^3$ の係数が正だから,グラフは下図のようになる。
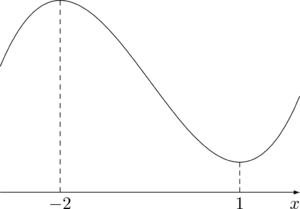
$x=-2,~1$ のとき
&f(-2)=-8+6+12-3=7 \\[4pt]
&f(1)=1+\dfrac{3}{2}-6-3=-\dfrac{13}{2}
\end{align*}

3次関数のグラフの等間隔性と12分の1公式を利用しよう。
$f'(-1)=3-3-6=-6$ より,$l$ の方程式は
&y=-6(x+1)+\dfrac{7}{2} \\[4pt]
&y=-6x-\dfrac{5}{2}
\end{align*}
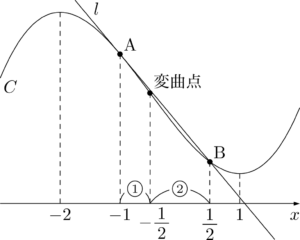
$C$ と $l$ で囲まれた図形は下図の赤色部分になる。
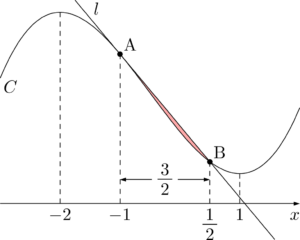

最初の問題でもやったように,割り算を利用して解いても良い。
x^3+\dfrac{3}{2}x^2-6x-3=(x+1)^2\left(x-\dfrac{1}{2}\right)-6x-\dfrac{5}{2}
\end{align*}
y=-6x-\dfrac{5}{2}
\end{align*}

では,次の(3)に進もう。

3次関数のグラフの等間隔性を利用して,接点の $x$ 座標を求めよう。
点Aから $C$ に $l$ と異なる接線 $m$ を引いたとき,接点をCとすると下図のようになる。
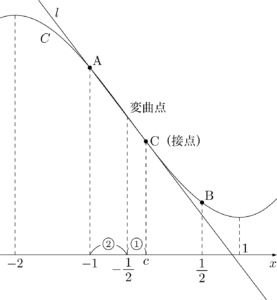
点Cの $x$ 座標を $c$ とすると
c=\dfrac{3\times\left(-\dfrac{1}{2}\right)-1\Cdot(-1)}{3-1}=-\dfrac{1}{4}
\end{align*}
f’\left(-\dfrac{1}{4}\right)=3\Cdota\dfrac{7}{4}\left(-\dfrac{5}{4}\right)=-\dfrac{105}{16}
\end{align*}
&y=-\dfrac{105}{16}(x+1)+\dfrac{7}{2} \\[4pt]
&y=-\dfrac{105}{16}x-\dfrac{49}{16}
\end{align*}

最後の接点Cの $x$ 座標を求める部分は「12分の1公式の応用」の $2:1:3$ の法則を利用して求めても良い。
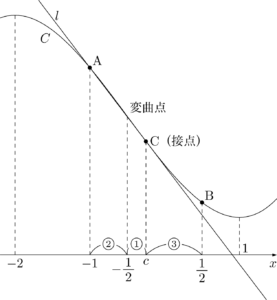
点Cの $x$ 座標は2点A, Bの中点の $x$ 座標に等しいから
c=\dfrac{-1+\dfrac{1}{2}}{2}=-\dfrac{1}{4}
\end{align*}
3次関数のグラフと接する放物線で囲まれた図形の面積

最後にもう1問。3次関数とそれに接する放物線で囲まれた図形の面積に関する問題を解いてみよう。
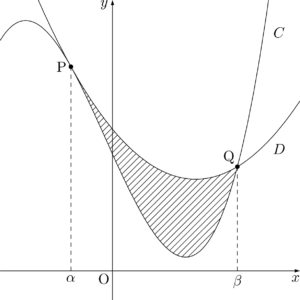
S&=\dint{\alpha}{\beta}\{px^2+qx+r-(ax^3+bx^2+cx+d)\}\;dx \\[4pt]
&=-\dint{\alpha}{\beta}a(x-\alpha)^2(x-\beta)\;dx \\[4pt]
&=\dint{\beta}{\alpha}a(x-\alpha)^2(x-\beta)\;dx\\[4pt]
&=\dfrac{a}{12}(\beta-\alpha)^4
\end{align*}

単にグラフの見た目だけで公式を覚えるのではなく,「接する」「交わる」といった言葉から被積分関数がどのようになるかを考えることで,12分の1公式が使えるかどうかを判断できるようにしよう。
まとめ

3次関数のグラフとその接線で囲まれた図形の面積は12分の1公式で求められることを覚えておこう。

また,3次関数のグラフとそれに接する放物線で囲まれた図形の面積も同様に12分の1公式になることも当たり前だと思えるようにしよう。

2次関数のグラフに関する12分の1公式やその他の時短テクニックについては,次の記事で学習しよう。