ここでは円と放物線の共有点について説明します。
この記事では,放物線の軸が円の中心を通っている状況について扱うことにします。
「円と放物線の共有点」の問題を苦手とする人が多いですが,落ち着いて考えることができるようになりましょう。
Contents
円と放物線の共有点の個数

ヒロ
円と放物線の共有点の個数は,円と放物線の位置関係によって決まる。

ヒロ
ただし,放物線の頂点は原点で下に凸であるは動かないものとし,円の中心は放物線の軸上を動く状態を考えるものとする。

ヒロ
円の中心の $y$ 座標の符号で場合分けをして,円と放物線の共有点の個数を分類する。
円の中心のy座標が負のとき

ヒロ
円と放物線の共有点の個数を分類すると,次のようになる。
【円と放物線の共有点の個数】
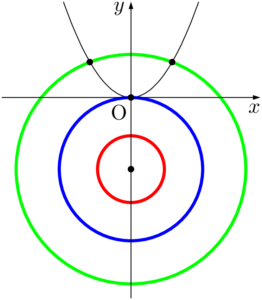
下図のように,円と放物線の共有点の個数は0,1,2のいずれかである。
下図のように,円と放物線の共有点の個数は0,1,2のいずれかである。
- 赤い円のとき,共有点は0個
- 青い円のとき,共有点は1個
- 緑の円のとき,共有点は2個
円の中心のy座標が正のとき

ヒロ
上と同じように,円と放物線の共有点の個数を分類すると,次のようになる。
【円と放物線の共有点の個数】
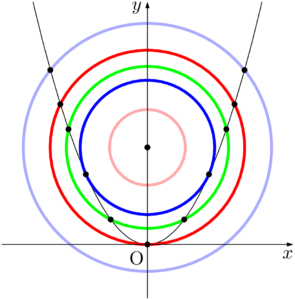
下図のように,円と放物線の共有点の個数は0,2,3,4のいずれかである。
下図のように,円と放物線の共有点の個数は0,2,3,4のいずれかである。
- ピンクの円のとき,共有点は0個
- 青い円と水色の円のとき,共有点は2個
- 赤い円のとき,共有点は3個
- 緑の円のとき,共有点は4個