Contents
円と放物線の共有点の個数に関する問題【立命館大】
2010年 立命館大$a$ を定数として,放物線 $y=x^2+2$ と円 $x^2+(y-a)^2=9$ が異なる2点で接するとき,$a=\myhako$ となる。また,この放物線と円が異なる4点で交わるような定数 $a$ の値の範囲は,$\myhako<a<\myhako$ である。
【前半の考え方と解答】
$y=x^2+2~\cdots\cdots①$,$x^2+(y-a)^2=9~\cdots\cdots②$ とする。 ①と②より,$y$ を消去すると
\begin{align*} &x^2+(x^2+2-a)^2=9 \\[4pt] &x^4+(5-2a)x^2+a^2-4a-5=0~\cdots\cdots③ \end{align*}
放物線①と円②が異なる2点で接するのは,方程式③が異なる2つの重解をもつときであり,$x^2=X$ とおいた方程式 \begin{align*} X^2+(5-2a)X+a^2-4a-5=0 \end{align*}
が正の重解をもつときである。判別式を $D$ とすると \begin{align*} \begin{cases} D=(5-2a)^2-4(a^2-4a-5)=0 &\cdots\cdots④ \\[4pt] -(5-2a)>0 &\cdots\cdots⑤ \end{cases} \end{align*}
④より \begin{align*} &-4a+45=0 \\[4pt] &a=\dfrac{45}{4} \end{align*}
⑤より,$a>\dfrac{5}{2}$ となるから,$a=\dfrac{45}{4}$ は条件をみたす。この放物線と円が異なる4点で交わるような定数 $a$ の値の範囲は,$\myhako<a<\myhako$ である。
【後半の考え方と解答】
放物線①と円②が異なる4点で交わるのは,方程式③が異なる4つの実数解をもつときであり,
\begin{align*} X^2+(5-2a)X+a^2-4a-5=0 \end{align*}
が異なる2つの正の解をもつときである。よって \begin{align*} \begin{cases} D=(5-2a)^2-4(a^2-4a-5)>0 &\cdots\cdots⑥ \\[4pt] -(5-2a)>0 &\cdots\cdots⑤ \\[4pt] a^2-4a-5>0 &\cdots\cdots⑦ \end{cases} \end{align*}
⑥より\begin{align*} &-4a+45>0 \\[4pt] &a<\dfrac{45}{4} \end{align*}
⑤より,$a>\dfrac{5}{2}$⑦より,
\begin{align*} &(a-5)(a+1)>0 \\[4pt] &a<-1,~5<a \end{align*}
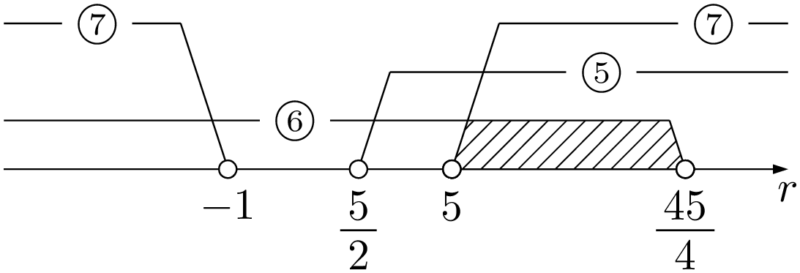
以上より,$5<a<\dfrac{45}{4}$
円と放物線の共有点の個数に関する問題【岩手大】
2016年 岩手大放物線 $y=x^2$ と円 $x^2+(y-3)^2=\dfrac{r^2}{4}$ について,次の問いに答えよ。ただし,$r$ は正の定数である。
(1) $r=6$ のとき,放物線と円の共有点の座標をすべて求めよ。
(2) $r$ がすべての正の実数値をとって変化するとき,放物線と円の共有点の個数はどのように変わるか,調べよ。
(1) $r=6$ のとき,放物線と円の共有点の座標をすべて求めよ。
(2) $r$ がすべての正の実数値をとって変化するとき,放物線と円の共有点の個数はどのように変わるか,調べよ。
【(1)の考え方と解答】
$y=x^2~\cdots\cdots①$,$x^2+(y-3)^2=\dfrac{r^2}{4}~\cdots\cdots②$ とする。
$r=6$ のとき,①と②より $x$ を消去すると
よって,求める共有点の座標は
$y=x^2~\cdots\cdots①$,$x^2+(y-3)^2=\dfrac{r^2}{4}~\cdots\cdots②$ とする。
$r=6$ のとき,①と②より $x$ を消去すると
\begin{align*}
&y+(y-3)^2=\dfrac{36}{4} \\[4pt]
&y^2-5y=0 \\[4pt]
&y(y-5)=0 \\[4pt]
&y=0,~5
\end{align*}
①より,$y=0$ のとき,$x=0$ であり,$y=5$ のとき,$x=\pm\sqrt{5}$ である。&y+(y-3)^2=\dfrac{36}{4} \\[4pt]
&y^2-5y=0 \\[4pt]
&y(y-5)=0 \\[4pt]
&y=0,~5
\end{align*}
よって,求める共有点の座標は
\begin{align*}
(0,~0),~(\sqrt{5},~5),~(-\sqrt{5},~5)
\end{align*}
(0,~0),~(\sqrt{5},~5),~(-\sqrt{5},~5)
\end{align*}
(2) $r$ がすべての正の実数値をとって変化するとき,放物線と円の共有点の個数はどのように変わるか,調べよ。
【(2)の考え方と解答】
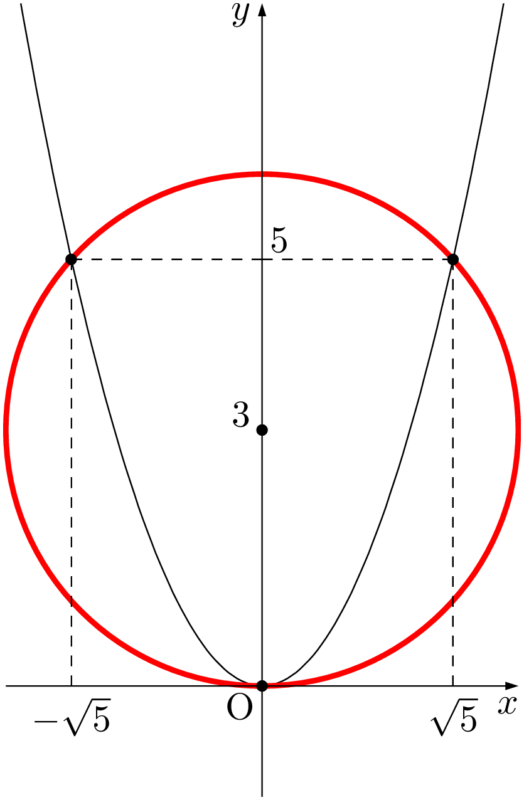
(1)の $r=6$ のときの放物線①と円②の共有点は3個あり,次の図のようになる。円②を赤色で描いている。
次に,放物線②と円①が原点以外で接する $r$ の値を求める。これは
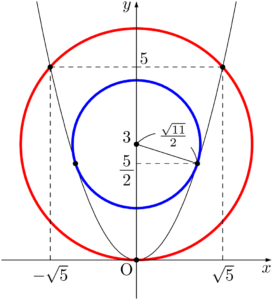
$r=6$ のときの円②を赤色で,$r=\sqrt{11}$ のときの円②を青色で描くと次のようになる。円②の半径は $\dfrac{r}{2}$ であることに注意しよう。
円②の中心は変わらず,$r$ の値に応じて半径が変化して,共有点の個数も変化する。
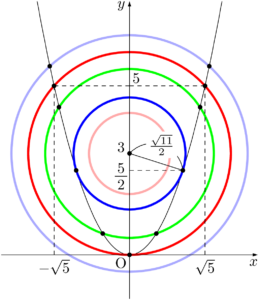
したがって,放物線①と円②の共有点の個数は,次のように分類することができる。
(1)の $r=6$ のときの放物線①と円②の共有点は3個あり,次の図のようになる。円②を赤色で描いている。

次に,放物線②と円①が原点以外で接する $r$ の値を求める。これは
\begin{align*}
&y+(y-3)^2=\dfrac{r^2}{4} \\[4pt]
&y^2-5y+9-\dfrac{r^2}{4}=0
\end{align*}
が正の重解をもつときである。判別式を $D$ とすると&y+(y-3)^2=\dfrac{r^2}{4} \\[4pt]
&y^2-5y+9-\dfrac{r^2}{4}=0
\end{align*}
\begin{align*}
&D=25-4\left(9-\dfrac{r^2}{4}\right)=0 \\[4pt]
&-11+r^2=0 \\[4pt]
&r=\pm\sqrt{11}
\end{align*}
$r>0$ より,$r=\sqrt{11}$ である。このとき,重解は $y=\dfrac{5}{2}$ である。&D=25-4\left(9-\dfrac{r^2}{4}\right)=0 \\[4pt]
&-11+r^2=0 \\[4pt]
&r=\pm\sqrt{11}
\end{align*}
$r=6$ のときの円②を赤色で,$r=\sqrt{11}$ のときの円②を青色で描くと次のようになる。円②の半径は $\dfrac{r}{2}$ であることに注意しよう。

円②の中心は変わらず,$r$ の値に応じて半径が変化して,共有点の個数も変化する。

したがって,放物線①と円②の共有点の個数は,次のように分類することができる。
- ピンクの円のとき,0個
- 青い円のとき,2個
- 緑の円のとき,4個
- 赤い円のとき,3個
- 水色の円のとき,2個
円の半径は $\dfrac{r}{2}$ であることに注意して,それぞれの色の円になる $r$ の値や範囲を考えると,次のようになる。
\begin{align*} &0<r<\sqrt{11}~のとき,0個 \\[4pt] &r=\sqrt{11}~のとき,2個 \\[4pt] &\sqrt{11}<r<6~のとき,4個 \\[4pt] &r=6~のとき,3個 \\[4pt] &6<r~のとき,2個 \end{align*}


















