Contents
円と放物線の共有点を求める問題【金沢大】
2016年 金沢大平面上の2つの曲線
\begin{align*}
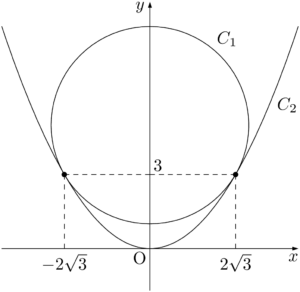
C_1:x^2+(y-5)^2=16,~C_2:y=\dfrac{1}{4}x^2
\end{align*}
を考える。$C_1$ と $C_2$ の共有点の座標を求めよ。C_1:x^2+(y-5)^2=16,~C_2:y=\dfrac{1}{4}x^2
\end{align*}
【考え方と解答】
$x^2+(y-5)^2=16~\cdots\cdots①$,$y=\dfrac{1}{4}x^2~\cdots\cdots②$ とする。
②を①に代入して
よって,求める共有点は $(-2\sqrt{3},~3),~(2\sqrt{3},~3)$
$x^2+(y-5)^2=16~\cdots\cdots①$,$y=\dfrac{1}{4}x^2~\cdots\cdots②$ とする。
②を①に代入して
\begin{align*}
&x^2+\left(\dfrac{1}{4}x^2-5\right)^2=16 \\[4pt]
&\dfrac{1}{16}x^4-\dfrac{3}{2}x^2+9=0 \\[4pt]
&\left(\dfrac{1}{4}x^2-3\right)^2=0 \\[4pt]
&x^2=12 \\[4pt]
&x=\pm2\sqrt{3}
\end{align*}
②より,$x=\pm2\sqrt{3}$ のとき,$y=3$&x^2+\left(\dfrac{1}{4}x^2-5\right)^2=16 \\[4pt]
&\dfrac{1}{16}x^4-\dfrac{3}{2}x^2+9=0 \\[4pt]
&\left(\dfrac{1}{4}x^2-3\right)^2=0 \\[4pt]
&x^2=12 \\[4pt]
&x=\pm2\sqrt{3}
\end{align*}
よって,求める共有点は $(-2\sqrt{3},~3),~(2\sqrt{3},~3)$


ヒロ
$x$ を消去する方法でも解いておく。
【別の考え方と解答】
$x^2+(y-5)^2=16~\cdots\cdots①$,$y=\dfrac{1}{4}x^2~\cdots\cdots②$ とする。
②より,$x^2=4y$
これを①に代入すると
$x^2+(y-5)^2=16~\cdots\cdots①$,$y=\dfrac{1}{4}x^2~\cdots\cdots②$ とする。
②より,$x^2=4y$
これを①に代入すると
\begin{align*}
&4y+(y-5)^2=16 \\[4pt]
&y^2-6y+9=0 \\[4pt]
&(y-3)^2=0 \\[4pt]
&y=3
\end{align*}
②に代入して&4y+(y-5)^2=16 \\[4pt]
&y^2-6y+9=0 \\[4pt]
&(y-3)^2=0 \\[4pt]
&y=3
\end{align*}
\begin{align*}
&\dfrac{1}{4}x^2=3 \\[4pt]
&x^2=12 \\[4pt]
&x=\pm2\sqrt{3}
\end{align*}
よって,求める共有点は $(-2\sqrt{3},~3),~(2\sqrt{3},~3)$&\dfrac{1}{4}x^2=3 \\[4pt]
&x^2=12 \\[4pt]
&x=\pm2\sqrt{3}
\end{align*}

ヒロ
いま,2つの曲線 $C_1$ と $C_2$ は2つの共有点をもつが,その $y$ 座標が等しいため,$x$ を消去すると重解になる。

ヒロ
共有点の個数を求める問題の場合「$y$ が1つしか求まらないから,共有点も1つだ」と考えてしまわないようにしよう。

ヒロ
$y$ 座標としては1つしか出てこないけど,2つの曲線はともに $y$ 軸に関して対称であるから,共有点は2個あることに注意しよう。


















