Contents
円と直線の位置関係の問題【北海学園大】
2018年 北海学園大円 $(x-1)^2+y^2=1$ と直線 $3x+4y+k=0$ が共有点をもたないとき,定数 $k$ の値の範囲を求めよ。
【考え方と解答】
円と直線が共有点をもたないのは,円の中心から直線までの距離が半径より大きいときである。円の中心 $(1,~0)$ から直線 $3x+4y+k=0$ までの距離を $d$ とすると
円と直線が共有点をもたないのは,円の中心から直線までの距離が半径より大きいときである。円の中心 $(1,~0)$ から直線 $3x+4y+k=0$ までの距離を $d$ とすると
\begin{align*}
d&=\dfrac{\abs{3\Cdot1+4\Cdot0+k}}{\sqrt{3^2+4^2}} \\[4pt]
&=\dfrac{\abs{k+3}}{5}
\end{align*}
円の半径は1であるから,条件をみたすのは $d>1$ となるときである。d&=\dfrac{\abs{3\Cdot1+4\Cdot0+k}}{\sqrt{3^2+4^2}} \\[4pt]
&=\dfrac{\abs{k+3}}{5}
\end{align*}
\begin{align*}
&\dfrac{\abs{k+3}}{5}>1 \\[4pt]
&\abs{k+3}>5 \\[4pt]
&k+3<-5,~5<k+3 \\[4pt] &k<-8,~2<k \end{align*}
&\dfrac{\abs{k+3}}{5}>1 \\[4pt]
&\abs{k+3}>5 \\[4pt]
&k+3<-5,~5<k+3 \\[4pt] &k<-8,~2<k \end{align*}
円と直線の接点に関する問題【久留米大】
2020年 久留米大・医$k$ を正の定数とし,座標平面上で表される円 $C:x^2+y^2-8x-10y+36=0$,直線 $l:2x-y+k=0$ を考える。
(1) 円 $C$ の中心の座標は $\left(\myhako,~\myhako\right)$ であり,半径は $\sqrt{\myhako}$ である。
(2) 直線 $l$ が円 $C$ に接するとき,$k=\myhako$ であり,直線 $l$ と円 $C$ の接点の座標は $\left(\myhako,~\myhako\right)$ である。
(1) 円 $C$ の中心の座標は $\left(\myhako,~\myhako\right)$ であり,半径は $\sqrt{\myhako}$ である。
(2) 直線 $l$ が円 $C$ に接するとき,$k=\myhako$ であり,直線 $l$ と円 $C$ の接点の座標は $\left(\myhako,~\myhako\right)$ である。
【(1)の考え方と解答】
基本形に変形して求めよう。
基本形に変形して求めよう。
\begin{align*}
&(x-4)^2+(y-5)^2=5
\end{align*}
よって,円 $C$ の中心の座標は $(4,~5)$ であり,半径は $\sqrt{5}$ である。&(x-4)^2+(y-5)^2=5
\end{align*}
(2) 直線 $l$ が円 $C$ に接するとき,$k=\myhako$ であり,直線 $l$ と円 $C$ の接点の座標は $\left(\myhako,~\myhako\right)$ である。
【(2)の考え方と解答】
(1)で円の中心の座標を求めているから,点と直線の距離を利用して,$l$ と $C$ が接するときの $k$ の値を求めよう。$l$ と $C$ が接するとき,円 $C$ の中心 $(4,~5)$ と直線 $l$ との距離が $\sqrt{5}$ になるから
(1)で円の中心の座標を求めているから,点と直線の距離を利用して,$l$ と $C$ が接するときの $k$ の値を求めよう。$l$ と $C$ が接するとき,円 $C$ の中心 $(4,~5)$ と直線 $l$ との距離が $\sqrt{5}$ になるから
\begin{align*}
&\dfrac{\abs{8-5+k}}{\sqrt{5}}=\sqrt{5} \\[4pt]
&\abs{k+3}=5 \\[4pt]
&k+3=\pm5 \\[4pt]
&k=-8,~2
\end{align*}
$k$ は正の定数であるから,$k=2$&\dfrac{\abs{8-5+k}}{\sqrt{5}}=\sqrt{5} \\[4pt]
&\abs{k+3}=5 \\[4pt]
&k+3=\pm5 \\[4pt]
&k=-8,~2
\end{align*}

ヒロ
次は接点の座標を求めよう。

ヒロ
ここで,円 $C$ の方程式と直線 $l$ の方程式を連立させて解くのは少し面倒に感じるだろう。

ヒロ
そこで,一度問題から離れて,少し楽に求める方法を考えることにする。
【円と直線の接点の求め方】
円 $C$ と直線 $l$ が接する状態の一例を図示すると,次のようになる。ただし,$C$ と $l$ の接点をTとする。
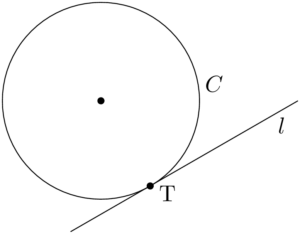
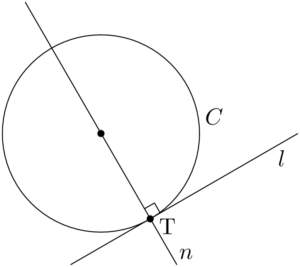
ここで,円の中心と接点Tを通る直線 $n$ は直線 $l$ と直交することに着目すると,接点Tは2直線 $l,~n$ の交点と捉えることができる。ちなみに,この直線 $n$ を点Tにおける円 $C$ の法線という。

ヒロ
(2)の解答を仕上げよう。
【(2)の考え方と解答の続き】
$k=2$ のとき,直線 $l$ の方程式は $2x-y+2=0~\cdots\cdots①$ である。
接点における円 $C$ の法線と直線 $l$ の交点を求めることで接点の座標を求めよう。円の中心 $(4,~5)$ を通り,直線 $l$ に垂直な直線の方程式は
よって,求める接点の座標は $(2,~6)$

$k=2$ のとき,直線 $l$ の方程式は $2x-y+2=0~\cdots\cdots①$ である。
接点における円 $C$ の法線と直線 $l$ の交点を求めることで接点の座標を求めよう。円の中心 $(4,~5)$ を通り,直線 $l$ に垂直な直線の方程式は
\begin{align*}
&(x-4)+2(y-5)=0 \\[4pt]
&x+2y-14=0~\cdots\cdots②
\end{align*}
$①\times2+②$ より&(x-4)+2(y-5)=0 \\[4pt]
&x+2y-14=0~\cdots\cdots②
\end{align*}
\begin{align*}
&5x-10=0 \\[4pt]
&x=2
\end{align*}
①より,$y=6$&5x-10=0 \\[4pt]
&x=2
\end{align*}
よって,求める接点の座標は $(2,~6)$


ヒロ
当たり前であるが,円 $C$ の方程式と直線 $l$ の方程式を連立させて考えても同じ結果が得られる。
【(2)の別の考え方】
$l:2x-y+k=0$ より,$y=2x+k$
これを $C:x^2+y^2-8x-10y+36=0$ に代入すると
$k=2$ のとき,$D=0$ であるから③は重解をもつ。③の重解は $x=-\dfrac{2k-14}{5}$ と表されるから,$k=2$ を代入して
よって,求める接点の座標は $(2,~6)$
$l:2x-y+k=0$ より,$y=2x+k$
これを $C:x^2+y^2-8x-10y+36=0$ に代入すると
\begin{align*}
&x^2+(2x+k)^2-8x-10(2x+k)+36=0 \\[4pt]
&5x^2+2(2k-14)x+k^2-10k+36=0~\cdots\cdots③
\end{align*}
③の判別式を $D$ とすると,$C$ と $l$ が接するのは $D=0$ のときであるから&x^2+(2x+k)^2-8x-10(2x+k)+36=0 \\[4pt]
&5x^2+2(2k-14)x+k^2-10k+36=0~\cdots\cdots③
\end{align*}
\begin{align*}
&D/4=(2k-14)^2-5(k^2-10k+36)=0 \\[4pt]
&k^2+6k-16=0 \\[4pt]
&(k+8)(k-2)=0 \\[4pt]
&k=-8,~2
\end{align*}
$k>0$ であるから,$k=2$&D/4=(2k-14)^2-5(k^2-10k+36)=0 \\[4pt]
&k^2+6k-16=0 \\[4pt]
&(k+8)(k-2)=0 \\[4pt]
&k=-8,~2
\end{align*}
$k=2$ のとき,$D=0$ であるから③は重解をもつ。③の重解は $x=-\dfrac{2k-14}{5}$ と表されるから,$k=2$ を代入して
\begin{align*}
x=-\dfrac{4-14}{5}=2
\end{align*}
となる。$x=2$ を $l:y=2x+2$ に代入して,$y=6$x=-\dfrac{4-14}{5}=2
\end{align*}
よって,求める接点の座標は $(2,~6)$

ヒロ
上では,③の重解をサクッと求めたが,③に $k=2$ を代入して,次のように2次方程式を解き直す人もいるだろう。
【③を解き直す】
③に $k=2$ を代入すると
③に $k=2$ を代入すると
\begin{align*}
&5x^2-20x+20=0 \\[4pt]
&x^2-4x+4=0 \\[4pt]
&(x-2)^2=0 \\[4pt]
&x=2
\end{align*}
&5x^2-20x+20=0 \\[4pt]
&x^2-4x+4=0 \\[4pt]
&(x-2)^2=0 \\[4pt]
&x=2
\end{align*}

ヒロ
答えを求めることだけを目的とするのであれば,③を解き直す方法で何も悪くない。

ヒロ
しかし,多くの参考書や問題集では,このような解法では解かれてなく,最初に書いた方法で解かれていることが多いだろう。

ヒロ
そして,その解答を理解できずに苦しんでいる人もいる。

ヒロ
理解できない部分は「③の重解が $x=-\dfrac{2k-14}{5}$ となる」部分だろう。

ヒロ
これを理解して使えるようにしよう。
【2次方程式の重解】
円と直線が接するときを考えているから,判別式 $D$ が0になることは理解しているはず。ここで解の公式を思い出そう。
2次方程式 $ax^2+bx+c=0$ の解は
\begin{align*}
x=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}
\end{align*}
と表される。ここで判別式を $D$ とすると,$D=b^2-4ac$ であるから,解の公式は $D$ を用いてx=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}
\end{align*}
\begin{align*}
x=\dfrac{-b\pm\sqrt{D}}{2a}
\end{align*}
と表される。これに $D=0$ を代入するとx=\dfrac{-b\pm\sqrt{D}}{2a}
\end{align*}
\begin{align*}
x=-\dfrac{b}{2a}
\end{align*}
となる。2次方程式が重解をもつとき,その重解を求める方法としてよく使われる式である。x=-\dfrac{b}{2a}
\end{align*}
ちなみに,2次方程式の実数解は放物線と $x$ 軸の共有点の $x$ 座標としても得られる。このことを考えると,2次方程式 $ax^2+bx+c=0$ が重解をもつのは,$y=ax^2+bx+c$ のグラフが $x$ 軸に接するときで,その接点は頂点と一致する。次の図は $a>0$ のときの例。
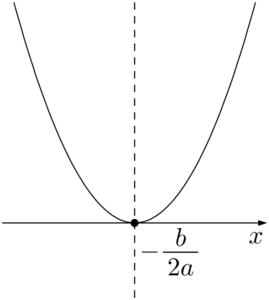
つまり,軸の方程式が $x=-\dfrac{b}{2a}$ であるから,接点の $x$ 座標も $-\dfrac{b}{2a}$ ということになる。
また,2次関数の軸の方程式については,平方完成することなく瞬時に出せる(言える)ようにするべきである。
したがって,この問題で調べたい③の重解の場合は,次の2次方程式③
\begin{align*}
5x^2+2(2k-14)x+k^2-10k+36=0
\end{align*}
の $x^2$ と $x$ の係数を見て,重解は $x=-\dfrac{2k-14}{5}$ となることが分かる。5x^2+2(2k-14)x+k^2-10k+36=0
\end{align*}

ヒロ
接点の座標を求めるのは少し面倒な計算であるが,ベクトルを利用すると,また別の方法も考えられる。

ヒロ
それについては,ベクトルの記事で触れることにする。