問題文を一見したときにすぐに「同じものを含む順列の問題だ」と分からないものもあります。
有名な問題として最短経路の総数を求める問題が挙げられます。
経路の総数を矢印の順列の総数として捉える考え方を身に付けましょう。
Contents
最短経路の総数を求める問題

ヒロ
実際に定期テストで出題された次の問題を考えてみよう。
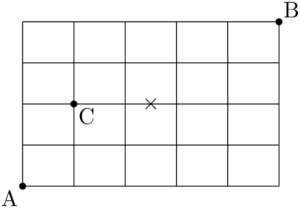
問題次の図のような街路で,AからBまで行く最短経路のうち,次のような場合は何通りあるか。
(1) 総数
(2) Cを通る経路
(3) ×印の箇所を通らない経路
(1) 総数
(2) Cを通る経路
(3) ×印の箇所を通らない経路

【(1)の考え方と総数】
AからBまで行く最短経路を考えるということは,上方向か右方向にしか進めない。
最短経路の1つを具体的に考えると次のような経路がある。
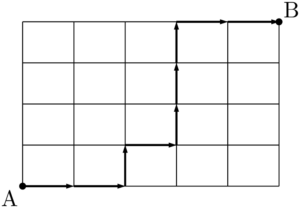
上の経路を矢印を用いると
「→→↑→↑↑↑→→」
と表すことができる。つまり,「→」と「↑」の2種類の矢印を並べることで1つの経路が決まることになる。したがって,5つの→と4つの↑の並べ方の総数が最短経路の総数であるから
矢印を並べる場所を用意して,9か所から↑を入れる4か所を選ぶと考えて $\nCk{9}{4}$ 通りとしても良い。階乗を使うか $\nCk{n}{k}$ を使うかはそれぞれの好みのため,どちらでも良い。
AからBまで行く最短経路を考えるということは,上方向か右方向にしか進めない。
最短経路の1つを具体的に考えると次のような経路がある。

上の経路を矢印を用いると
「→→↑→↑↑↑→→」
と表すことができる。つまり,「→」と「↑」の2種類の矢印を並べることで1つの経路が決まることになる。したがって,5つの→と4つの↑の並べ方の総数が最短経路の総数であるから
\begin{align*}
\dfrac{9!}{5!4!}&=\dfrac{9\Cdot8\Cdot7\Cdot6}{4\Cdot3\Cdot2\Cdot1} \\[4pt]&=126~通り
\end{align*}
\dfrac{9!}{5!4!}&=\dfrac{9\Cdot8\Cdot7\Cdot6}{4\Cdot3\Cdot2\Cdot1} \\[4pt]&=126~通り
\end{align*}
矢印を並べる場所を用意して,9か所から↑を入れる4か所を選ぶと考えて $\nCk{9}{4}$ 通りとしても良い。階乗を使うか $\nCk{n}{k}$ を使うかはそれぞれの好みのため,どちらでも良い。
(2) Cを通る経路
【(2)の考え方と解答】
Cを通る経路は次の手順で決めることができる。
① AからCまで行く。
② CからBまで行く。
①の方法は→, ↑, ↑の並べ方を考えて $\dfrac{3!}{2!}$ 通りあり,②の方法は4つの→と2つの↑の並べ方を考えて $\dfrac{6!}{4!2!}$ 通りあるから,
Cを通る経路は次の手順で決めることができる。
① AからCまで行く。
② CからBまで行く。
①の方法は→, ↑, ↑の並べ方を考えて $\dfrac{3!}{2!}$ 通りあり,②の方法は4つの→と2つの↑の並べ方を考えて $\dfrac{6!}{4!2!}$ 通りあるから,
\begin{align*}
\dfrac{3!}{2!}\times\dfrac{6!}{4!2!}&=3\times15=45~通り
\end{align*}
\dfrac{3!}{2!}\times\dfrac{6!}{4!2!}&=3\times15=45~通り
\end{align*}
(3) ×印の箇所を通らない経路
【(3)の考え方と解答】
(2)からも分かるように,×印を通らない経路より,×印を通る経路の総数の方が求めやすい。次の図のように2点P, Qを定める。
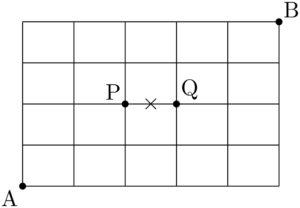
×印を通る経路は次の手順で決めることができる。
① AからPまで行く。
② PからQまで行く。
③ QからBまで行く。
①の方法は $\dfrac{4!}{2!2!}$ 通りあり,②の方法は1通りある。③の方法は $\dfrac{4!}{2!2!}$ 通りあるから,×印を通る経路の総数は
(2)からも分かるように,×印を通らない経路より,×印を通る経路の総数の方が求めやすい。次の図のように2点P, Qを定める。

×印を通る経路は次の手順で決めることができる。
① AからPまで行く。
② PからQまで行く。
③ QからBまで行く。
①の方法は $\dfrac{4!}{2!2!}$ 通りあり,②の方法は1通りある。③の方法は $\dfrac{4!}{2!2!}$ 通りあるから,×印を通る経路の総数は
\begin{align*}
\dfrac{4!}{2!2!}\times1\times\dfrac{4!}{2!2!}&=\dfrac{4\Cdot3}{2}\times\dfrac{4\Cdot3}{2} \\[4pt]&=36~通り
\end{align*}
よって,×印を通らない経路の総数は\dfrac{4!}{2!2!}\times1\times\dfrac{4!}{2!2!}&=\dfrac{4\Cdot3}{2}\times\dfrac{4\Cdot3}{2} \\[4pt]&=36~通り
\end{align*}
\begin{align*}
126-36=90~通り
\end{align*}
126-36=90~通り
\end{align*}
最短経路の総数を求める問題2

ヒロ
次も実際に定期テストで出題された問題。
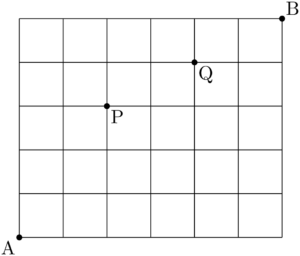
問題次の図のような街路がある。次の場合,AからBまで最短距離で行く道順は何通りあるか。
(1) AからBへ行く。
(2) AからPを通ってBへ行く。
(3) AからP, Qを通ってBへ行く。
(4) AからP, Qを通らないでBへ行く。
(1) AからBへ行く。
(2) AからPを通ってBへ行く。
(3) AからP, Qを通ってBへ行く。
(4) AからP, Qを通らないでBへ行く。


ヒロ
この問題では $\nCk{n}{k}$ を使って解答することにする。
【(1)の考え方と解答】
矢印を並べる考え方で解こう。
6個の→と5個の↑を並べる方法の総数に等しいから
矢印を並べる考え方で解こう。
6個の→と5個の↑を並べる方法の総数に等しいから
\begin{align*}
\nCk{11}{5}&=\dfrac{11\Cdot10\Cdot9\Cdot8\Cdot7}{5\Cdot4\Cdot3\Cdot2\Cdot1} \\[4pt]&=462~通り
\end{align*}
\nCk{11}{5}&=\dfrac{11\Cdot10\Cdot9\Cdot8\Cdot7}{5\Cdot4\Cdot3\Cdot2\Cdot1} \\[4pt]&=462~通り
\end{align*}
(2) AからPを通ってBへ行く。
【(2)の考え方と解答】
次の2つの手順で考える。
① AからPまで行く。
② PからBまで行く。
①の方法が $\nCk{5}{2}$ 通りあり,②の方法が $\nCk{6}{2}$ 通りあるから,
次の2つの手順で考える。
① AからPまで行く。
② PからBまで行く。
①の方法が $\nCk{5}{2}$ 通りあり,②の方法が $\nCk{6}{2}$ 通りあるから,
\begin{align*}
\nCk{5}{2}\times\nCk{6}{2}=10\times15 \\[4pt]&=150~通り
\end{align*}
\nCk{5}{2}\times\nCk{6}{2}=10\times15 \\[4pt]&=150~通り
\end{align*}
(3) AからP, Qを通ってBへ行く。
【(3)の考え方と解答】
次の3つの手順で考える。
① AからPまで行く。
② PからQまで行く。
③ QからBまで行く。
①の方法が $\nCk{5}{2}$ 通りあり,②の方法が $\nCk{3}{1}$ 通りあり,③の方法が $\nCk{3}{1}$ 通りあるから,
次の3つの手順で考える。
① AからPまで行く。
② PからQまで行く。
③ QからBまで行く。
①の方法が $\nCk{5}{2}$ 通りあり,②の方法が $\nCk{3}{1}$ 通りあり,③の方法が $\nCk{3}{1}$ 通りあるから,
\begin{align*}
\nCk{5}{2}\times\nCk{3}{1}\times\nCk{3}{1}&=10\times3\times3 \\[4pt]&=90~通り
\end{align*}
\nCk{5}{2}\times\nCk{3}{1}\times\nCk{3}{1}&=10\times3\times3 \\[4pt]&=90~通り
\end{align*}
(4) AからP, Qを通らないでBへ行く。
【(4)の考え方と解答】
P, Qを通る経路の総数をそれぞれ $n(P),~n(Q)$ とすると,求める場合の数は $n(\overline{P}\cap\overline{Q})$ である。
ド・モルガンの法則より,$n(\overline{P\cup Q})$ である。ベン図で表すと次の斜線部分を表す。
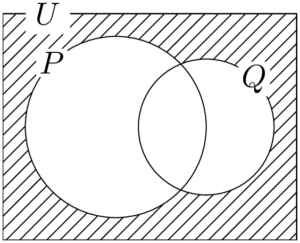
「○○を通る経路の総数」の方が求めやすいから,$n(P\cup Q)$ を求める。ここで
$n(Q)$ はAからQを通ってBへ行く経路の総数を表すから,(2)と同様に考えて
以上より,
P, Qを通る経路の総数をそれぞれ $n(P),~n(Q)$ とすると,求める場合の数は $n(\overline{P}\cap\overline{Q})$ である。
ド・モルガンの法則より,$n(\overline{P\cup Q})$ である。ベン図で表すと次の斜線部分を表す。

「○○を通る経路の総数」の方が求めやすいから,$n(P\cup Q)$ を求める。ここで
\begin{align*}
n(P\cup Q)=n(P)+n(Q)-n(P\cap Q)
\end{align*}
であることを利用する。$n(P)$ はAからPを通ってBへ行く経路の総数を表すから,(2)より150通り。n(P\cup Q)=n(P)+n(Q)-n(P\cap Q)
\end{align*}
$n(Q)$ はAからQを通ってBへ行く経路の総数を表すから,(2)と同様に考えて
\begin{align*}
\nCk{8}{4}\times\nCk{3}{1}&=\dfrac{8\Cdot7\Cdot6\Cdot5}{4\Cdot3\Cdot2\Cdot1}\times3 \\[4pt]&=210~通り
\end{align*}
$n(P\cap Q)$ はAからP, Qを通ってBへ行く経路の総数を表すから,(3)より90通り。\nCk{8}{4}\times\nCk{3}{1}&=\dfrac{8\Cdot7\Cdot6\Cdot5}{4\Cdot3\Cdot2\Cdot1}\times3 \\[4pt]&=210~通り
\end{align*}
以上より,
\begin{align*}
n(P\cup Q)&=n(P)+n(Q)-n(P\cap Q) \\[4pt]&=150+210-90 \\[4pt]&=270
\end{align*}
したがって,求める経路の総数はn(P\cup Q)&=n(P)+n(Q)-n(P\cap Q) \\[4pt]&=150+210-90 \\[4pt]&=270
\end{align*}
\begin{align*}
462-270=192~通り
\end{align*}
462-270=192~通り
\end{align*}

ヒロ
最短経路の問題なんて簡単だと思っていると,「最短経路ではない経路の総数」を求める問題が出題されることもあるので注意しよう。

ヒロ
一度は経験しておかないと白紙解答になるかもしれないので,次の記事で知識を吸収しておこう。





















