Contents
円と直線の位置関係の判別

ヒロ
図が描かれておらず,円と直線のそれぞれの方程式だけが与えられた場合は,計算をしないと位置関係を把握することはできない。

ヒロ
図を正確に描くことで,位置関係を把握することができると思っている人が多いが,これは間違っている。

ヒロ
すごく拡大してようやく分かるくらいギリギリ交わってないということもあるから,図の見た目をそれほど信用するべきではない。

ヒロ
したがって,円と直線の位置関係を調べるときは,計算して判断することになる。

ヒロ
その方法として2つ考えられるので,順番に説明する。
円の中心から直線の距離を調べる

ヒロ
円と直線の位置関係を,円の中心と直線との距離で調べる。
【円と直線が2点で交わるとき】
2点で交わる円と直線の例を図示すると,次のようになる。
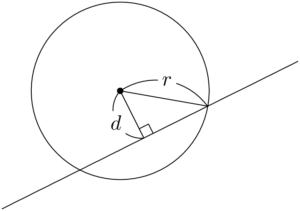
円の半径を $r$,円と直線の距離を $d$ とすると,$0<d<r$ が成り立つ。
【円と直線が接するとき】
1点で接する円と直線の例を図示すると,次のようになる。
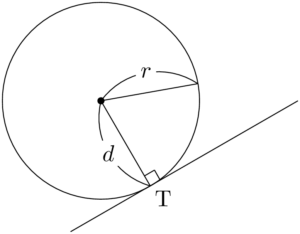

円の半径を $r$,円と直線の距離を $d$ とすると,$d=r$ が成り立つ。
【円と直線が共有点をもたないとき】
共有点をもたない円と直線の例を図示すると,次のようになる。
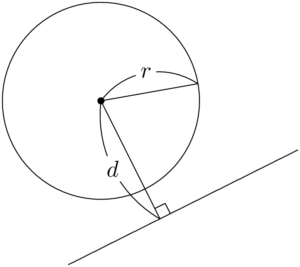

円の半径を $r$,円と直線の距離を $d$ とすると,$d>r$ が成り立つ。

ヒロ
与えられた円の方程式から,円の中心と半径 $r$ を求めることができる。さらに,円の中心と与えられた直線までの距離 $d$ も求めることができる。

ヒロ
あとは $d$ と $r$ を比べることで,円と直線の位置関係を把握することができる。
連立方程式の解を調べる

ヒロ
円と直線の位置関係を,円の方程式と直線の方程式を連立させた方程式の解で調べる。
円
\begin{align*} C:x^2+y^2+lx+my+n=0~\cdots\cdots① \end{align*}
と直線 $l:ax+by+c=0~\cdots\cdots②$ の位置関係を調べる。①と②を連立して $y$ を消去すると,$x$ の2次方程式が得られる。その2次方程式を
\begin{align*}
px^2+qx+r=0~\cdots\cdots③
\end{align*}
とすると,③の実数解は円 $C$ と直線 $l$ の共有点の $x$ 座標を表す。したがって,③の実数解の個数を調べることで,円と直線の共有点の個数を調べることができ,③の判別式を $D$ とすると次のようになる。
px^2+qx+r=0~\cdots\cdots③
\end{align*}
- ③が異なる2つの実数解をもつとき($D>0$),共有点は2個である。
- ③が重解をもつとき($D=0$),共有点は1個である。
- ③が実数解をもたないとき($D<0$),共有点はない。