大学入試問題で出題される円には,直線に接する円,放物線に接する円,円に接する円など,様々な円がありますが,ここでは座標軸に接する円の方程式について説明します。
円が座標軸に接するときに,何が言えるのかをしっかり理解しましょう。
Contents
座標軸に接する円

ヒロ
座標軸に接する円には,次の3パターンがある。
- $x$ 軸に接する
- $y$ 軸に接する
- $x$ 軸と $y$ 軸の両方に接する
【座標軸に接する円】
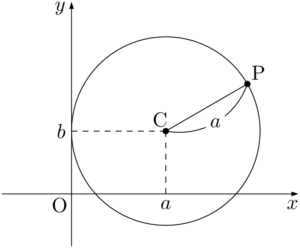
$x$ 軸に接する円の方程式を考える。円の中心を $(a,~b)$,半径を $r$ とする。円の中心が第1象限または第2象限にあるときは,$r=b$ であり,第3象限または第4象限にあるときは $r=-b$ である。円の中心の位置に関係なく,$r^2=b^2$ が成り立つから,$x$ 軸に接する円の方程式は
\begin{align*}
(x-a)^2+(y-b)^2=b^2
\end{align*}
と表せる。(x-a)^2+(y-b)^2=b^2
\end{align*}

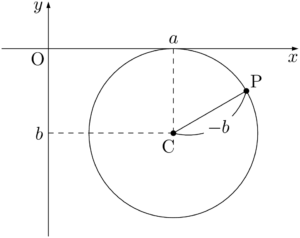
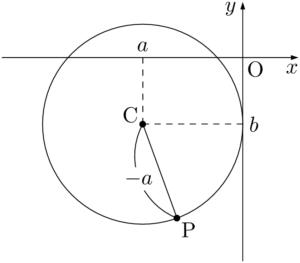
次に $y$ 軸に接する円の方程式を考える。円の中心を $(a,~b)$,半径を $r$ とする。円の中心が第1象限または第4象限にあるときは,$r=a$ であり,第2象限または第3象限にあるときは $r=-a$ である。円の中心の位置に関係なく,$r^2=a^2$ が成り立つから,$y$ 軸に接する円の方程式は
\begin{align*}
(x-a)^2+(y-b)^2=a^2
\end{align*}
と表せる。(x-a)^2+(y-b)^2=a^2
\end{align*}
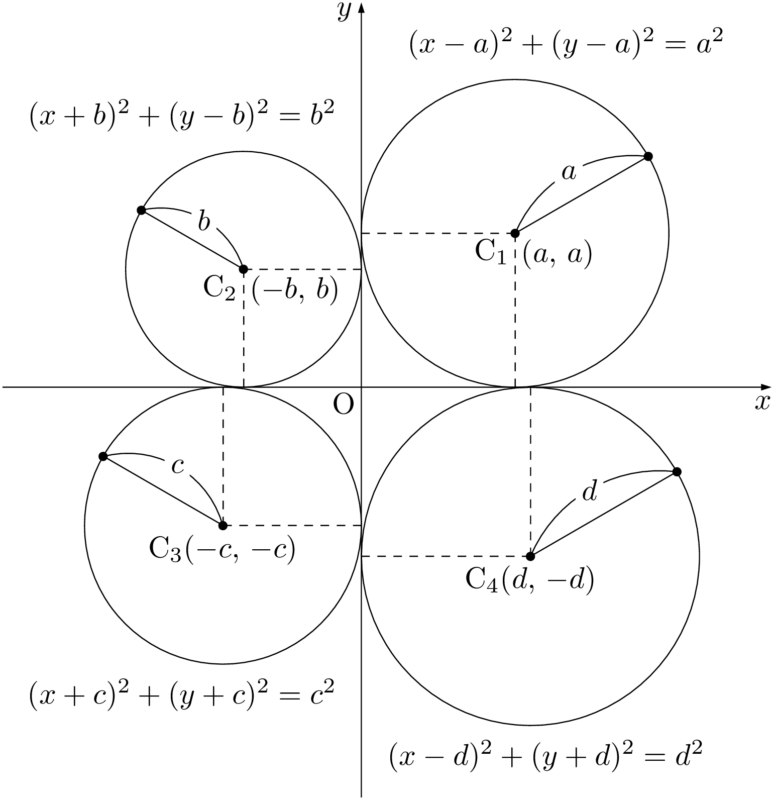
最後に,両座標軸に接する円を考える。両座標軸までの距離が半径と等しくなるから,円の中心の $x$ 座標,$y$ 座標の絶対値はともに半径と等しくなる。したがって,円の方程式は
\begin{align*}
(x\pm a)^2+(y\pm a)^2=a^2~(複号任意)
\end{align*}
と表せる。$a,~b,~c,~d$ を正の数として両座標軸に接する円を4種類描くと次のようになる。(x\pm a)^2+(y\pm a)^2=a^2~(複号任意)
\end{align*}