ここでは2次関数に関する応用問題を解説します。
様々な問題を解くことによって,それぞれの問題の考え方を身に付けましょう。
2変数関数の最小値を求める問題

ヒロ
実際に定期テストで出題された問題を解いてみよう。
問題$x,~y$ を変数とする関数 $z=x^2-6xy+10y^2+2y$ について,$z$ の最小値とそのときの $x,~y$ の値を求めよ。
【考え方と解答】
2つの変数があるときは,どちらか1つの文字に着目して考えよう。今回は $x$ と $y$ のどちらに着目しても2次関数だから,2次の係数をみて判断する。$x^2$ の係数が1だから,$x$ に着目する。$x$ に着目した時点で $y$ を定数をみることになる。$z$ を平方完成すると次のようになる。
したがって,$z$ は $x=3y$ かつ $y=-1$ のときに最小となる。すなわち,$x=-3,~y=-1$ のときに最小値 $-1$ をとる。
2つの変数があるときは,どちらか1つの文字に着目して考えよう。今回は $x$ と $y$ のどちらに着目しても2次関数だから,2次の係数をみて判断する。$x^2$ の係数が1だから,$x$ に着目する。$x$ に着目した時点で $y$ を定数をみることになる。$z$ を平方完成すると次のようになる。
\begin{align*}
z&=x^2-6yx+10y^2+2y \\[4pt]
&=(x-3y)^2+y^2+2y
\end{align*}
この時点で $x=3y$ のとき,$z$ は最小値 $y^2+2y$ をとることが分かる。$y$ が定数ならこれで終わりであるが,実際には変数であるから,$y^2+2y$ の最小値を考える。z&=x^2-6yx+10y^2+2y \\[4pt]
&=(x-3y)^2+y^2+2y
\end{align*}
\begin{align*}
y^2+2y=(y+1)^2-1
\end{align*}
となるから,$y^2+2y$ は $y=-1$ のときに最小値 $-1$ をとることが分かる。y^2+2y=(y+1)^2-1
\end{align*}
したがって,$z$ は $x=3y$ かつ $y=-1$ のときに最小となる。すなわち,$x=-3,~y=-1$ のときに最小値 $-1$ をとる。
2変数関数の最小値を求める問題2

ヒロ
実際に定期テストで出題された問題を知ることで,どの程度の問題を解けるようにならないといけないのかを知ろう。
問題$x^2+y^2=5$ のとき,$2x+y^2$ の最大値と最小値を求めよ。また,そのときの $x,~y$ の値を求めよ。

ヒロ
どちらかの文字を消去して1変数関数にしよう。
【考え方と解答】
$x$ と $y$ のどちらを消去するかを考えたとき,$y^2=-x^2+5$ として $2x+y^2$ に代入すると $x$ の2次関数になることが分かる。つまり,$y$ を消去することになる。$z=2x+y^2$ とおくと
$x$ と $y$ のどちらを消去するかを考えたとき,$y^2=-x^2+5$ として $2x+y^2$ に代入すると $x$ の2次関数になることが分かる。つまり,$y$ を消去することになる。$z=2x+y^2$ とおくと
\begin{align*}
z&=2x+(-x^2+5) \\[4pt]
&=-x^2+2x+5 \\[4pt]
&=-(x-1)^2+6
\end{align*}
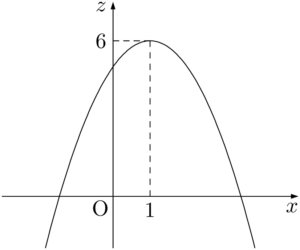
となるから,グラフは次のような上に凸の放物線になる。z&=2x+(-x^2+5) \\[4pt]
&=-x^2+2x+5 \\[4pt]
&=-(x-1)^2+6
\end{align*}


ヒロ
「$x=1$ のときに最大となり,最小値はない」としてしまうと不正解である。

ヒロ
少し難しいが,$x$ の定義域に注意するようにしよう。

ヒロ
いま $x$ と $y$ は $x^2+y^2=5$ をみたすような $x,~y$ である。

ヒロ
$x$ と $y$ がすべての実数を取り得るかどうかを考えると,そんなことはないと分かるはず。

ヒロ
例えば,$x=10$ とすると,$100+y^2=5$ となり,$y^2=-95$ となる。2乗して $-95$ になる実数は存在しないから,$x=10$ になることはないと分かる。

ヒロ
「実数」とは「2乗すると0以上になる数」と意識しておこう。
【考え方と解答】
$y^2=-x^2+5$ と変形した時点で $x$ の定義域を調べておこう。
$y^2\geqq0$ であるから
$x=1$ のとき,$y^2=4$ であるから $y=\pm2$
$x=-\sqrt{5}$ のとき,$y^2=0$ であるから $y=0$
したがって,求める最大値と最小値は次のようになる。
最大値 6 $(x,~y)=(1,~\pm2)$ のとき
最小値 $-2\sqrt5$ $(x,~y)=(-\sqrt{5},~0)$ のとき
$y^2=-x^2+5$ と変形した時点で $x$ の定義域を調べておこう。
$y^2\geqq0$ であるから
\begin{align*}
&-x^2+5\geqq0 \\[4pt]
&x^2\leqq5 \\[4pt]
&-\sqrt{5}\leqq x\leqq\sqrt{5}
\end{align*}
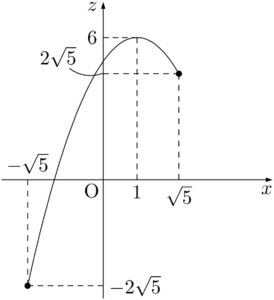
ということで,正しいグラフは次のようになる。&-x^2+5\geqq0 \\[4pt]
&x^2\leqq5 \\[4pt]
&-\sqrt{5}\leqq x\leqq\sqrt{5}
\end{align*}

$x=1$ のとき,$y^2=4$ であるから $y=\pm2$
$x=-\sqrt{5}$ のとき,$y^2=0$ であるから $y=0$
したがって,求める最大値と最小値は次のようになる。
最大値 6 $(x,~y)=(1,~\pm2)$ のとき
最小値 $-2\sqrt5$ $(x,~y)=(-\sqrt{5},~0)$ のとき
絶対値記号を含む方程式の実数解の個数を求める問題

ヒロ
次も実際に定期テストで出題された問題。
問題方程式 $\abs{x^2-x-2}+2x=k$($k$ は定数)の実数解の個数を求めよ。

ヒロ
グラフを利用して求めよう。
【考え方と解答】
$y=\abs{x^2-x-2}+2x$ と $y=k$ のグラフの共有点の個数を調べる。
絶対値を外すために中身が0以上になる範囲を求める。
グラフより,求める実数解の個数は次のようになる。
$y=\abs{x^2-x-2}+2x$ と $y=k$ のグラフの共有点の個数を調べる。
絶対値を外すために中身が0以上になる範囲を求める。
\begin{align*}
&x^2-x-2\geqq0 \\[4pt]
&(x-2)(x+1)\geqq0 \\[4pt]
&x\leqq-1,~2\leqq x
\end{align*}
これで絶対値を外せる。&x^2-x-2\geqq0 \\[4pt]
&(x-2)(x+1)\geqq0 \\[4pt]
&x\leqq-1,~2\leqq x
\end{align*}
\begin{align*}
y&=\begin{cases}
(x^2-x-2)+2x &~(x\leqq-1,~2\leqq x)\\[4pt]
-(x^2-x-2)+2x &~(-1\leqq x\leqq2)
\end{cases} \\[4pt]
&=\begin{cases}
x^2+x-2 &~(x\leqq-1,~2\leqq x)\\[4pt]
-x^2+3x+2 &~(-1\leqq x\leqq2)
\end{cases} \\[4pt]
&=\begin{cases}
\left(x+\dfrac{1}{2}\right)^2-\dfrac{9}{4} &~(x\leqq-1,~2\leqq x) \\[4pt]
-\left(x-\dfrac{3}{2}\right)^2+\dfrac{17}{4} &~(-1\leqq x\leqq2)
\end{cases}
\end{align*}
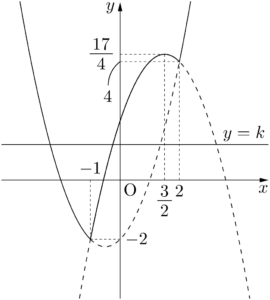
$y=\abs{x^2-x-2}+2x$ のグラフと $y=k$ のグラフとの共有点を調べる。y&=\begin{cases}
(x^2-x-2)+2x &~(x\leqq-1,~2\leqq x)\\[4pt]
-(x^2-x-2)+2x &~(-1\leqq x\leqq2)
\end{cases} \\[4pt]
&=\begin{cases}
x^2+x-2 &~(x\leqq-1,~2\leqq x)\\[4pt]
-x^2+3x+2 &~(-1\leqq x\leqq2)
\end{cases} \\[4pt]
&=\begin{cases}
\left(x+\dfrac{1}{2}\right)^2-\dfrac{9}{4} &~(x\leqq-1,~2\leqq x) \\[4pt]
-\left(x-\dfrac{3}{2}\right)^2+\dfrac{17}{4} &~(-1\leqq x\leqq2)
\end{cases}
\end{align*}

グラフより,求める実数解の個数は次のようになる。
\begin{align*} &k<-2~のとき~~0 \\[4pt] &k=-2~のとき~~1 \\[4pt] &-2<k<4~のとき~~2 \\[4pt] &k=4~のとき~~3 \\[4pt] &4<k<\dfrac{17}{4}~のとき~~4 \\[4pt] &k=\dfrac{17}{4}~のとき~~3 \\[4pt] &\dfrac{17}{4}<k~のとき~~2 \end{align*}


















