Contents
2直線の垂直条件

ヒロ
それでは,2直線が垂直になる条件を考える。
基本形の2直線の垂直条件

ヒロ
直線の方程式が基本形で表されているときは,すぐに傾きが分かる。

ヒロ
2つの直線の傾きから,2直線が垂直になる条件を考える。
【2直線が垂直になる条件】
直交する2直線 $l,~m$ の方程式をそれぞれ $l:y=ax+b$,$m:y=cx+d~(a>0,~c<0)$ とし,$l,~m$ の交点をPとする。点Pとの距離が1となる $x$ 軸と垂直な直線と2直線 $l,~m$ との交点をそれぞれQ,Rとする。
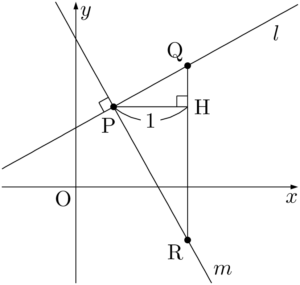
$l$ の傾きが $a$ であるから,$\text{QH}=a$ である。また,$m$ の傾きが $c$ であるから $\text{RH}=-c$ である。$\sankaku{PQH}$ と $\sankaku{PRH}$ はともに直角三角形であるから,三平方の定理より
直交する2直線 $l,~m$ の方程式をそれぞれ $l:y=ax+b$,$m:y=cx+d~(a>0,~c<0)$ とし,$l,~m$ の交点をPとする。点Pとの距離が1となる $x$ 軸と垂直な直線と2直線 $l,~m$ との交点をそれぞれQ,Rとする。

$l$ の傾きが $a$ であるから,$\text{QH}=a$ である。また,$m$ の傾きが $c$ であるから $\text{RH}=-c$ である。$\sankaku{PQH}$ と $\sankaku{PRH}$ はともに直角三角形であるから,三平方の定理より
\begin{align*} &\text{PQ}^2=\text{QH}^2+\text{PH}^2=a^2+1 \\[4pt] &\text{PR}^2=\text{RH}^2+\text{PH}^2=c^2+1 \end{align*}
さらに $\sankaku{PQR}$ が直角三角形であるときを考えて \begin{align*} &\text{PQ}^2+\text{PR}^2=\text{QR}^2 \\[4pt] &(a^2+1)+(c^2+1)=(a-c)^2 \\[4pt] &a^2+c^2+2=a^2-2ac+c^2 \\[4pt] &ac=-1 \end{align*}

ヒロ
これより,2直線が直交するときは,2直線の傾きの積が $-1$ であることが分かる。
2直線の垂直条件:基本形 2直線 $l,~m$ の方程式がそれぞれ $l:y=ax+b$,$m:y=cx+d$ であるとき,$l$ と $m$ が垂直になるのは,2直線の傾きの積が $-1$ になるときである。すなわち $ac=-1$ のときである。

切片形の2直線の垂直条件

ヒロ
切片形で表された2直線が垂直になる条件を考える。

ヒロ
2直線の傾きの積が $-1$ になることを利用しよう。
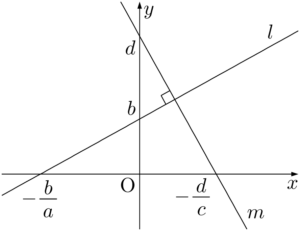
2直線の垂直条件:切片形 2直線 $l,~m$ の方程式をそれぞれ $l:\dfrac{x}{a}+\dfrac{y}{b}=1$,$m:\dfrac{x}{c}+\dfrac{y}{d}=1$ とする。$l$ と $m$ が垂直になるのは,2直線の傾きの積が $-1$ であるときだから
\begin{align*}
&-\dfrac{b}{a}\times\left(-\dfrac{d}{c}\right)=-1 \\[4pt]
&ac+bd=0
\end{align*}
&-\dfrac{b}{a}\times\left(-\dfrac{d}{c}\right)=-1 \\[4pt]
&ac+bd=0
\end{align*}
一般形の2直線の垂直条件

ヒロ
一般形で表された2直線が垂直になる条件を考える。

ヒロ
直線の方程式の $x$ の係数や $y$ の係数が0の場合は,座標軸に平行な直線となり,垂直かどうかは簡単に分かるため,そうでない場合を考える。
2直線の垂直条件:一般形 2直線 $l,~m$ の方程式がそれぞれ $l:ax+by+c=0$,$m:px+qy+r=0$ であるとき,$l$ と $m$ が垂直になるのは,それぞれの傾き $-\dfrac{a}{b}$ と $-\dfrac{p}{q}$ の積が $-1$ になるときである。
\begin{align*}
&-\dfrac{a}{b}\times\left(-\dfrac{p}{q}\right)=-1 \\[4pt]
&ap+bq=0
\end{align*}
&-\dfrac{a}{b}\times\left(-\dfrac{p}{q}\right)=-1 \\[4pt]
&ap+bq=0
\end{align*}

ヒロ
このことを利用すると,直線の方程式が一般形で与えられていたとしても,基本形に変形することなく,その直線と垂直な直線の方程式を求めることができるようになる。
垂直な直線の方程式点 $(p,~q)$ を通り,直線 $ax+by+c=0$ と垂直な直線の方程式は
\begin{align*}
b(x-p)-a(y-q)=0
\end{align*}
である。b(x-p)-a(y-q)=0
\end{align*}


















