人を1列に並べるときにその両端や並べ方に条件が付くことがあります。
様々な問題の考え方を理解して解けるようにすることで,場合の数に対する嫌なイメージを払拭できるかもしれません。
少しずつ解ける問題を増やしていきましょう。
人を並べるときに両端に条件がある問題の考え方

ヒロ
次の問題を考えてみよう。
問題男子4人,女子3人が1列に並ぶとき,次の並び方は何通りあるか。
(1) 男女が交互に並ぶ。
(2) 両端が男子である。
(3) 少なくとも一端に女子がくる。
(4) 男子は男子,女子は女子で,それぞれ続いて並ぶ。
(1) 男女が交互に並ぶ。
(2) 両端が男子である。
(3) 少なくとも一端に女子がくる。
(4) 男子は男子,女子は女子で,それぞれ続いて並ぶ。
(1)の考え方と解答

ヒロ
まずは条件を満たすような並び方を考えよう。
【考え方と解答】
男女が交互に並ぶということは,男女男女男女男となる。
左から順に場合の数を考えると次のようになる。
男女が交互に並ぶということは,男女男女男女男となる。
左から順に場合の数を考えると次のようになる。
\begin{align*}
&男\to 女\to 男\to 女\to 男\to 女\to 男 \\[4pt]
&4\times3\times3\times2\times2\times1\times1 \\[4pt]
&=144~通り
\end{align*}
&男\to 女\to 男\to 女\to 男\to 女\to 男 \\[4pt]
&4\times3\times3\times2\times2\times1\times1 \\[4pt]
&=144~通り
\end{align*}

ヒロ
順に考えても解けるけど,式を書くのが少し面倒だから,次のように考えることで式が簡単になる。
【別の考え方と解答】
男子と女子を別々に1列に並べてから混ぜれば良い。
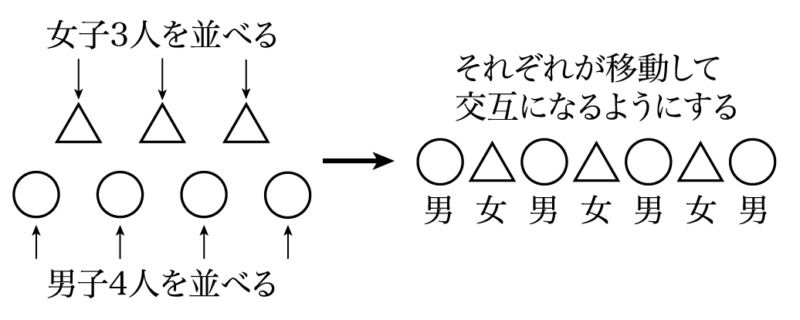
1つ1つの手順に分けると次のようになる。
① 男子4人を1列に並べる。
② 女子3人を1列に並べる。
③ 男子と女子が交互になるようにする。
①の方法は $4!$ 通りある。②の方法は $3!$ 通りある。③の方法は1通りある。
よって,求める場合の数は
男子と女子を別々に1列に並べてから混ぜれば良い。

1つ1つの手順に分けると次のようになる。
① 男子4人を1列に並べる。
② 女子3人を1列に並べる。
③ 男子と女子が交互になるようにする。
①の方法は $4!$ 通りある。②の方法は $3!$ 通りある。③の方法は1通りある。
よって,求める場合の数は
\begin{align*}
4!\times3!\times1=24\times6=144~通り
\end{align*}
4!\times3!\times1=24\times6=144~通り
\end{align*}
(2)の考え方と解答
男子4人,女子3人が1列に並ぶとき,両端が男子になる並び方
【考え方と解答】
条件の強い箇所から考える。
① 両端に男子2人を並べる。
② 間に残り5人を並べる。
①の方法は $4\Cdot3$ 通りある。②の方法は $5!$ 通りある。
よって,求める場合の数は
条件の強い箇所から考える。
① 両端に男子2人を並べる。
② 間に残り5人を並べる。
①の方法は $4\Cdot3$ 通りある。②の方法は $5!$ 通りある。
よって,求める場合の数は
\begin{align*}
4\Cdota3\times5!=12\times120=1440~通り
\end{align*}
4\Cdota3\times5!=12\times120=1440~通り
\end{align*}
(3)の考え方と解答
(3) 男子4人,女子3人が1列に並ぶとき,少なくとも一端に女子がくる並び方
【考え方と解答】
少なくとも一端に女子が来るということは
(i) 1つの端だけに女子がくる
(ii) 両端に女子がくる
の2つのタイプが考えられる。
(i)のときは次の手順で条件を満たすように並べることができる。
① 女子が来る端を決める。
② 端に来る女子を決める。
③ もう1つの端に来る男子を決める。
④ 間に残りの5人を並べる。
①の方法は2通りある。②の方法は3通りある。③の方法は4通りある。④の方法は $5!$ 通りある。
よって,このときの場合の数は
① 両端に2人の女子を並べる。
② 間に残りの5人を並べる。
①の方法は $3\Cdot2$ 通りある。②の方法は $5!$ 通りある。
よって,このときの場合の数は
少なくとも一端に女子が来るということは
(i) 1つの端だけに女子がくる
(ii) 両端に女子がくる
の2つのタイプが考えられる。
(i)のときは次の手順で条件を満たすように並べることができる。
① 女子が来る端を決める。
② 端に来る女子を決める。
③ もう1つの端に来る男子を決める。
④ 間に残りの5人を並べる。
①の方法は2通りある。②の方法は3通りある。③の方法は4通りある。④の方法は $5!$ 通りある。
よって,このときの場合の数は
\begin{align*}
2\times3\times4\times5!=2880~通り
\end{align*}
(ii)のときは次の手順で条件を満たすように並べることができる。2\times3\times4\times5!=2880~通り
\end{align*}
① 両端に2人の女子を並べる。
② 間に残りの5人を並べる。
①の方法は $3\Cdot2$ 通りある。②の方法は $5!$ 通りある。
よって,このときの場合の数は
\begin{align*}
3\Cdota2\times5!=720~通り
\end{align*}
(i), (ii)より3\Cdota2\times5!=720~通り
\end{align*}
\begin{align*}
2880+720=3600~通り
\end{align*}
2880+720=3600~通り
\end{align*}

ヒロ
「少なくとも」の言葉に反応して余事象を考えても良い。
【別の考え方と解答】
両端に女子が来ない,つまり両端が男子が来るときを考える。
(2)より,両端に男子が来る並び方は1440通り。
7人を1列に並べる方法は $7!$ 通りであるから,求める場合の数は
両端に女子が来ない,つまり両端が男子が来るときを考える。
(2)より,両端に男子が来る並び方は1440通り。
7人を1列に並べる方法は $7!$ 通りであるから,求める場合の数は
\begin{align*}
7!-1440=5040-1440=3600~通り
\end{align*}
7!-1440=5040-1440=3600~通り
\end{align*}

ヒロ
今回の場合は(2)で両端に男子がくる場合を求めているから再利用することで(3)が楽になる。

ヒロ
ただし,(2)が間違っていれば,自動的に(3)も間違えることになる。

ヒロ
したがって,時間に余裕があるのなら最初に示した解答のように直接求めて解答が一致することを確かめると完璧だろう。
(4)の考え方と解答
男子4人,女子3人が1列に並ぶとき,男子は男子,女子は女子で,それぞれ続く並び方

ヒロ
「隣り合う」と書かれていないけど,隣り合うような並び方の考えを利用することに気付こう。
【考え方と解答】
この問題では,男子4人は隣り合い,女子3人が隣り合うということ。
男子4人を○にして,女子3人を△にする。
① ○と△を並べる。
② ○の中の男子4人を並べる。
③ △の中の女子3人を並べる。
①の方法は $2!$ 通りある。②の方法は $4!$ 通りある。③の方法は $3!$ 通りある。
よって,求める場合の数は
この問題では,男子4人は隣り合い,女子3人が隣り合うということ。
男子4人を○にして,女子3人を△にする。
① ○と△を並べる。
② ○の中の男子4人を並べる。
③ △の中の女子3人を並べる。
①の方法は $2!$ 通りある。②の方法は $4!$ 通りある。③の方法は $3!$ 通りある。
よって,求める場合の数は
\begin{align*}
2!\times4!\times3!=2\times24\times6=288~通り
\end{align*}
2!\times4!\times3!=2\times24\times6=288~通り
\end{align*}



















