人を並べるときに「○○が隣り合う」や「○○が隣り合わない」という条件が付くことがあります。
そのようなときに,毎回どうするのかと悩んでいては時間制限の厳しい試験では,完答できないときがあります。
「○○が隣り合う」ときたらこう考えるという軸となる1つの考え方を持っていれば,適用できる問題に対してはスムーズに解くことができます。
そういった問題が苦手な人は,この記事を読んでヒトや文字を並べる問題を解けるようにしましょう。
「隣り合う」という条件がある並べ方の総数

ヒロ
まずは「隣り合う」という条件があるときの並べ方の総数の求め方を学習しよう。
問題男子3人,女子2人が1列に並ぶとき,女子2人が隣り合うような並び方は何通りあるか。
【考え方と解答】
分かりやすくするために,男子3人をA, B, C,女子2人をD, Eとする。
「女子2人が隣り合う」という条件を満たすような並び方を具体的に考えると,次のようなものがある。
ABCDE, ABCED, CADEB, BEDCA
いくつか書き出してみることで,当たり前だけどDとEを1つのカタマリになっていることを再認識することができる。
したがって,DとEを1つのカタマリでXとしてしまって考えると,次の2つの手順で条件を満たすように並べることができることが分かる。
① A, B, C, Xの4文字を1列に並べる。
② Xの中のDとEの並べ方を決める。
①の方法は $4!$ 通りあり,②の方法は $2!$ 通りあるから,全部で
分かりやすくするために,男子3人をA, B, C,女子2人をD, Eとする。
「女子2人が隣り合う」という条件を満たすような並び方を具体的に考えると,次のようなものがある。
ABCDE, ABCED, CADEB, BEDCA
いくつか書き出してみることで,当たり前だけどDとEを1つのカタマリになっていることを再認識することができる。
したがって,DとEを1つのカタマリでXとしてしまって考えると,次の2つの手順で条件を満たすように並べることができることが分かる。
① A, B, C, Xの4文字を1列に並べる。
② Xの中のDとEの並べ方を決める。
①の方法は $4!$ 通りあり,②の方法は $2!$ 通りあるから,全部で
\begin{align*}
4!\times2!=24\times2=48~通り
\end{align*}
4!\times2!=24\times2=48~通り
\end{align*}
「隣り合わない」という条件がある並べ方の総数

ヒロ
次に「隣り合わない」という条件があるときの並べ方の総数の求め方を学習しよう。
問題男子3人,女子2人が1列に並ぶとき,女子2人が隣り合わないような並び方は何通りあるか。

ヒロ
考え方が2パターンあるので1つずつ解説していく。
【余事象を利用する考え方と解答】
「隣り合わない」という否定形で書かれているので,条件の否定を考えると「隣り合う」となる。
つまり,女子2人が隣り合う場合を除けば,女子2人が隣り合わない場合になる。
男女合わせて5人を1列に並べる方法は $5!$ 通りあるから,求める場合の数は
「隣り合わない」という否定形で書かれているので,条件の否定を考えると「隣り合う」となる。
つまり,女子2人が隣り合う場合を除けば,女子2人が隣り合わない場合になる。
男女合わせて5人を1列に並べる方法は $5!$ 通りあるから,求める場合の数は
\begin{align*}
5!-4!\times2!=120-48=72~通り
\end{align*}
5!-4!\times2!=120-48=72~通り
\end{align*}

ヒロ
もう1つの考え方もマスターしよう。
【直接求める考え方と解答】
女子2人が隣り合わないということは,女子2人の間には少なくとも1人は男子が入るということ。
何人入るか分からないから,並べる順番を工夫する。つまり,次の2つの手順で条件を満たすように並べることができる。
① 男子3人を並べる。
② 並べた男子3人の間と両端の4か所のうち2か所に女子2人を並べる。
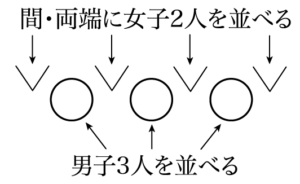
①の方法は $3!$ 通りある。②の方法は1人目の女子を配置する方法が4通りあり,その決め方に対して,2人目の女子を配置する方法が3通りある。
$\nPk{n}{r}$ を使うなら,$\nPk{4}{2}$ でも良いが,個人的には使わない。
よって,全部で
女子2人が隣り合わないということは,女子2人の間には少なくとも1人は男子が入るということ。
何人入るか分からないから,並べる順番を工夫する。つまり,次の2つの手順で条件を満たすように並べることができる。
① 男子3人を並べる。
② 並べた男子3人の間と両端の4か所のうち2か所に女子2人を並べる。

①の方法は $3!$ 通りある。②の方法は1人目の女子を配置する方法が4通りあり,その決め方に対して,2人目の女子を配置する方法が3通りある。
$\nPk{n}{r}$ を使うなら,$\nPk{4}{2}$ でも良いが,個人的には使わない。
よって,全部で
\begin{align*}3!\times4\Cdota3=72~通り\end{align*}
隣り合わないものが3つのときの並べ方の総数

ヒロ
隣り合わないものが3つになると,余事象を利用する考え方だと少し複雑になる。

ヒロ
例として次の問題を考えてみる。
問題男子4人,女子3人が1列に並ぶとき,どの女子も隣り合わないような並び方は何通りあるか。

ヒロ
隣り合う場合を除けば良いからといって,次のようにするのは間違いである。
【余事象を利用する間違った解答】
女子3人を1つのカタマリXとすると,男子4人とXを並べる方法が $5!$ 通りある。
Xの中の女子3人を並べる方法が $3!$ 通りあるから,女子3人が隣り合う並べ方の総数は
女子3人を1つのカタマリXとすると,男子4人とXを並べる方法が $5!$ 通りある。
Xの中の女子3人を並べる方法が $3!$ 通りあるから,女子3人が隣り合う並べ方の総数は
\begin{align*}
5!\times3!=120\times6=720~通り
\end{align*}
7人を1列に並べる方法は $7!=5040$ 通りあるから,求める場合の数は5!\times3!=120\times6=720~通り
\end{align*}
\begin{align*}
5040-720=4320~通り
\end{align*}
5040-720=4320~通り
\end{align*}

ヒロ
女子が3人いて「どの女子も隣り合わない」という条件だから,上の解答では3人全員が隣り合うときを除いているだけで,女子2人が隣り合う場合を除いていないのが間違いの原因だね。

ヒロ
上の解答の間違いを正しくするなら,女子2人が隣り合うときの場合の数を求める必要がある。
【余事象を利用する正しい解答】
(i) 女子3人が隣り合うとき
上のようにして720通り
(ii) 女子2人だけが隣り合うとき
女子2人のカタマリを□にして,もう1人の女子を△にする。次の手順で条件を満たすように並べることができる。
① 女子3人を□と△に並べる。
① 男子4人を並べる。
③ 並べた男子4人の間と両端の5か所から2か所を選んで□と△を並べる。
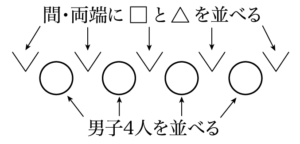
△の1人を決める方法が3通りあり,□になる2人の並べ方が $2!$ 通りあるから,①の方法は $3\Cdot2!$ 通りある。
②の方法は $4!$ 通りある。③の方法は $5\Cdot4$ 通りある。
したがって,女子が隣り合うときの場合の数は
(i) 女子3人が隣り合うとき
上のようにして720通り
(ii) 女子2人だけが隣り合うとき
女子2人のカタマリを□にして,もう1人の女子を△にする。次の手順で条件を満たすように並べることができる。
① 女子3人を□と△に並べる。
① 男子4人を並べる。
③ 並べた男子4人の間と両端の5か所から2か所を選んで□と△を並べる。

△の1人を決める方法が3通りあり,□になる2人の並べ方が $2!$ 通りあるから,①の方法は $3\Cdot2!$ 通りある。
②の方法は $4!$ 通りある。③の方法は $5\Cdot4$ 通りある。
したがって,女子が隣り合うときの場合の数は
\begin{align*}
3\Cdota2!\times4!\times5\Cdota4&=6\times24\times20 \\[4pt]&=2880~通り
\end{align*}
7人を1列に並べる方法は $7!=5040$ 通りあるから,求める場合の数は3\Cdota2!\times4!\times5\Cdota4&=6\times24\times20 \\[4pt]&=2880~通り
\end{align*}
\begin{align*}
5040-(720+2880)=1440~通り
\end{align*}
5040-(720+2880)=1440~通り
\end{align*}

ヒロ
隣り合わないものが3つあるときに「どれも隣り合わない」という条件では,2つが隣り合って,もう1つとは隣り合わない場合も除くことに注意しないといけない。

ヒロ
直接求める考え方もマスターしよう。
【直接求める考え方と解答】
次の手順で条件を満たすように並べることができる。
① 男子4人を並べる。
① 並べた男子4人の間と両端の5か所から3か所を選んで女子3人を並べる。
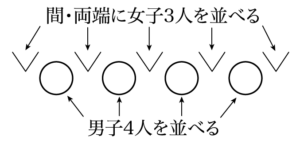
①の方法は $4!$ 通りある。②の方法は $5\Cdot4\Cdot3$ 通りある。
よって,求める場合の数は
次の手順で条件を満たすように並べることができる。
① 男子4人を並べる。
① 並べた男子4人の間と両端の5か所から3か所を選んで女子3人を並べる。

①の方法は $4!$ 通りある。②の方法は $5\Cdot4\Cdot3$ 通りある。
よって,求める場合の数は
\begin{align*}
4!\times5\Cdota4\Cdota3&=24\times60 \\[4pt]&=1440~通り
\end{align*}
4!\times5\Cdota4\Cdota3&=24\times60 \\[4pt]&=1440~通り
\end{align*}




















