式の変形や置換積分法で計算できない積で表された関数を積分するときは,部分積分法で積分しましょう。1回の部分積分で積分できるものもあれば,複数回の部分積分でようやく積分できるものもあります。
「瞬間部分積分」と呼ばれている積分法を用いることで,速く楽に積分することもできます。ここでは,最初に通常の部分積分法で不定積分を求め,その後に,瞬間部分積分による解法について説明します。

まずは次の問題を解いてみよう。
(1) $\dint{}{}x^3e^x\;dx$
(2) $\dint{}{}(x^2-2x)e^{-x}\;dx$
(3) $\dint{}{}\bigl(\log x\bigr)^3\;dx$
(4) $\dint{}{}x^3\log x\;dx$
Contents
部分積分法の公式の導出【logは常に微分側】

まずは,部分積分法の基本の確認をしておこう。

積の微分法を利用して,部分積分法の公式を導出しよう。
\bigl(f(x)g(x)\bigr)’=f'(x)g(x)+f(x)g'(x)
\end{align*}
f'(x)g(x)=\bigl(f(x)g(x)\bigr)’-f(x)g'(x)
\end{align*}
\dint{}{}f'(x)g(x)\,dx=f(x)g(x)-\dint{}{}f(x)g'(x)\,dx
\end{align*}
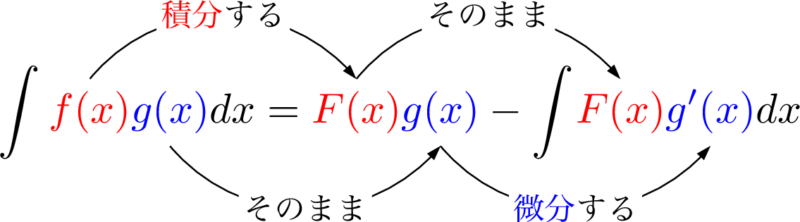
一般的に,何回か微分すると0になる方があればそちらが微分側である。ただし,$\log x$ は必ず微分側として扱う。
また,部分積分法を何回か繰り返し使うことによって,初めて基本関数に帰着される場合もあるので,1回であきらめてしまうのは禁物である。

まずは(1)の答え合わせからしよう。積分側を赤,微分側を青で書くよ。
&\dint{}{}{\color{blue}x^3}{\color{red}e^x}\,dx \\[4pt]
&={\color{blue}x^3}{\color{red}e^x}-\dint{}{}{\color{blue}3x^2}{\color{red}e^x}\,dx \\[4pt]
&=x^3e^x-\left({\color{blue}3x^2}{\color{red}e^x}-\dint{}{}{\color{blue}6x}{\color{red}e^x}\,dx\right) \\[4pt]
&=x^3e^x-3x^2e^x+\dint{}{}{\color{blue}6x}{\color{red}e^x}\,dx \\[4pt]
&=x^3e^x-3x^2e^x+{\color{blue}6x}{\color{red}e^x}-\dint{}{}{\color{blue}6}{\color{red}e^x}\,dx \\[4pt]
&=x^3e^x-3x^2e^x+6xe^x-6e^x+C \\[4pt]
&=(x^3-3x^2+6x-6)e^x+C
\end{align*}

積分側はずっと積分側で,微分側はずっと微分側なんですね。

そうだね。途中で入れ替えると,前の式に戻るので注意しよう。

それやったことあります。何をやってるんだ・・・って凹みます。

では続いて(2)の答え合わせをしよう。この問題は誤答が多い。もしも答えが次のようになっていたら,どこかで符号を間違えているはず。
&\dint{}{}({\color{blue}x^2-2x}){\color{red}e^{-x}}\,dx \\[4pt]
&=({\color{blue}x^2-2x})({\color{red}-e^{-x}})-\dint{}{}({\color{blue}2x-2})({\color{red}-e^{-x}})\,dx \\[4pt]
&=-(x^2-2x)e^{-x}-\left\{({\color{blue}2x-2}){\color{red}e^{-x}}-\dint{}{}{\color{blue}2}{\color{red}e^{-x}}\,dx\right\} \\[4pt]
&=-(x^2-2x)e^{-x}-(2x-2)e^{-x}+\dint{}{}2e^{-x}\;dx \\[4pt]
&=-(x^2-2x)e^{-x}-(2x-2)e^{-x}-2e^{-x}+C \\[4pt]
&=-\left\{(x^2-2x)+(2x-2)+2\right\}e^{-x}+C \\[4pt]
&=-x^2e^{-x}+C
\end{align*}

部分積分で答えが合わないときは,符号に注意してやり直そう!

見直すのはダメなんですか?

見直すより,もう一度やった方が速く合うと思うよ?答えが合ってから,間違えていた解答を見直すと,どこで間違えたかが分かるよね。その上で,自分がどこで間違えやすいかを覚えておこう。

はい,分かりました!

(3)は $1\Cdot\bigl(\log x\bigr)^3$ とみて,$\bigl(\log x\bigr)^3$ を微分側にしよう。
&\dint{}{}\bigl(\log x\bigr)^3\,dx \\[4pt]
&=\dint{}{}{\color{red}1}\Cdota{\color{blue}\bigl(\log x\bigr)^3}\;dx \\[4pt]
&={\color{red}x}{\color{blue}\bigl(\log x\bigr)^3}
-\dint{}{}{\color{red}x}\Cdota{\color{blue}3\bigl(\log x\bigr)^2\Cdota\dfrac1x}\,dx \\[4pt]
&=x\bigl(\log x\bigr)^3-\dint{}{}3\bigl(\log x\bigr)^2\;dx \\[4pt]
&=x\bigl(\log x\bigr)^3-\dint{}{}{\color{red}1}\Cdota{\color{blue}3\bigl(\log x\bigr)^2}\,dx \\[4pt]
&=x\bigl(\log x\bigr)^3-\left\{{\color{red}x}\Cdota{\color{blue}3\bigl(\log x\bigr)^2}
-\dint{}{}{\color{red}x}\Cdota{\color{blue}6\log x\Cdota\dfrac{1}{x}}\,dx\right\} \\[4pt]
&=x\bigl(\log x\bigr)^3-3x\bigl(\log x\bigr)^2+\dint{}{}6\log x\;dx \\[4pt]
&=x\bigl(\log x\bigr)^3-3x\bigl(\log x\bigr)^2+\dint{}{}{\color{red}1}\Cdota{\color{blue}6\log x}\;dx \\[4pt]
&=x\bigl(\log x\bigr)^3-3x\bigl(\log x\bigr)^2+{\color{red}x}\Cdota{\color{blue}6\log x}
-\dint{}{}{\color{red}x}\Cdota{\color{blue}6\Cdota\dfrac{1}{x}}\;dx \\[4pt]
&=x\bigl(\log x\bigr)^3-3x\bigl(\log x\bigr)^2+6x\log x-\dint{}{}6\;dx \\[4pt]
&=x\bigl(\log x\bigr)^3-3x\bigl(\log x\bigr)^2+6x\log x-6x+C \\[4pt]
&=\left\{\bigl(\log x\bigr)^3-3\bigl(\log x\bigr)^2+6\log x-6\right\}x+C
\end{align*}

最後の方は $\dint{}{}\log x\;dx=x\log x-x+C$ を覚えてサクッとやった方がいいね。
&\dint{}{}{\color{red}x^3}{\color{blue}\log x}\,dx \\[4pt]
&={\color{red}\dfrac14x^4}{\color{blue}\log x}-\dint{}{}{\color{red}\dfrac14x^4}\Cdota{\color{blue}\dfrac1x}\,dx \\[4pt]
&=\dfrac14x^4\log x-\dint{}{}\dfrac14x^3\,dx \\[4pt]
&=\dfrac14x^4\log x-\dfrac{1}{16}x^4+C
\end{align*}

中々大変でした・・・