Contents
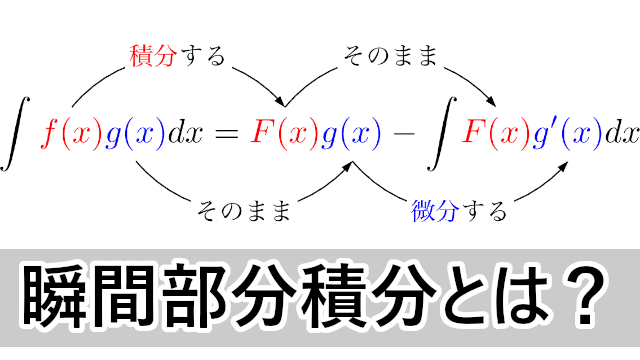
瞬間部分積分の公式

ヒロ
間違えずに積分する計算力は重要だけど,簡単に積分する方法も覚えておこう。

えっ?簡単な方法があるんですか?

なんでそれを先に教えてくれないんですか?

ヒロ
普通の方法もできずに,より高度な方法を習得しようとするのはおかしくない?

それもそうですね。

それって大分楽になりますか?

ヒロ
どう感じるかは個人差はあるけど,少なくとも僕にとっては劇的に楽になったと思う。

ヒロ
ということで部分積分が楽になる「瞬間部分積分」と呼ばれる方法を紹介するよ。
瞬間部分積分
\begin{align*}
\dint{}{}fg\;dx=fg_1-f’g_2+f^{\prime\prime}g_3-f^{\prime\prime\prime}g_4+\cdots
\end{align*}
ここで,$f$ は微分側で $g$ が積分側である。また,$g$ を積分するごとに $g_1,g_2,g_3$ と添字を増やしている。\dint{}{}fg\;dx=fg_1-f’g_2+f^{\prime\prime}g_3-f^{\prime\prime\prime}g_4+\cdots
\end{align*}

ヒロ
部分積分の仕組みを考えれば,理解はできると思う。

ヒロ
ただ,このままだとよく分からないと思うから,具体例を書いておくよ。
瞬間部分積分の公式
$f(x)$が整式であるとき,以下の形のものは,簡単に不定積分を求めることができる。

ヒロ
1番目と2番目の公式については,$\sin x$ や $\cos x$ は積分して符号を変えるのは微分するのと同じだから,最初だけ積分で,あとは両方微分すれば良いってことだよ。ただ,実際には積分して符号を変えるわけだから,$\sin x$ ではなく $\sin mx$ となっている場合は,順次 $m$ で割っていくことになる点に注意しよう。

ヒロ
5~8の4つが難しいと感じる人は,よく出てくる最初の1~4の4つだけに絞って,使えるようにすると良いよ。

ヒロ
(1)と(2)だけちょっと練習してみて?

はい!
【(1)を瞬間部分積分で楽に積分】
【(2)を瞬間部分積分で楽に積分】
\begin{align*}
(x^3)’=3x^2,~(3x^2)’=6x,~(6x)’=6
\end{align*}
であるから,(x^3)’=3x^2,~(3x^2)’=6x,~(6x)’=6
\end{align*}
\begin{align*}
\dint{}{}\ x^3e^x\;dx
&=(x^3-3x^2+6x-6)e^x+C
\end{align*}
\dint{}{}\ x^3e^x\;dx
&=(x^3-3x^2+6x-6)e^x+C
\end{align*}
【(2)を瞬間部分積分で楽に積分】
\begin{align*}
(x^2-2x)’=2x-2,~(2x-2)’=2
\end{align*}
であるから,(x^2-2x)’=2x-2,~(2x-2)’=2
\end{align*}
\begin{align*}
\dint{}{}\ (x^2-2x)e^{-x}\;dx
&=-\{(x^2-2x)+(2x-2)+2\}e^{-x}+C \\[4pt]
&=-x^2e^{-x}+C
\end{align*}
\dint{}{}\ (x^2-2x)e^{-x}\;dx
&=-\{(x^2-2x)+(2x-2)+2\}e^{-x}+C \\[4pt]
&=-x^2e^{-x}+C
\end{align*}

これは楽ですね!