Contents
2007年 九州大の入試問題の考え方
2007年 九州大自然数 $n$ に対して不等式
\begin{align*}
\log(n+1)<1+\dfrac{1}{2}+\dfrac{1}{3}+\cdots+\dfrac{1}{n}
\end{align*}
が成り立つことを示せ。\log(n+1)<1+\dfrac{1}{2}+\dfrac{1}{3}+\cdots+\dfrac{1}{n}
\end{align*}

ヒロ
最初の東北学院大の問題と似ているから同じように考えることができるね。

ヒロ
$\Sum{k=1}{n}\dfrac{1}{k}$ の方が大きいから,長方形が $y=\dfrac{1}{x}$ のグラフからはみ出る状態を考えよう。
$y=\dfrac{1}{x}$ のグラフは次のようになる。
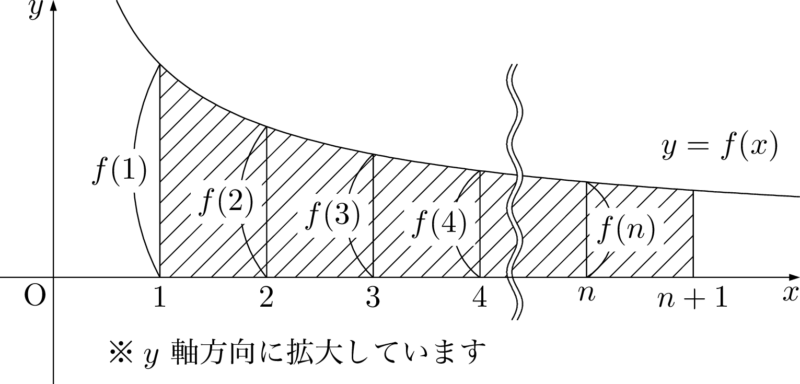
$y=\dfrac{1}{x}$ は単調に減少する関数であるから,$k\leqq x\leqq k+1$ において,$\dfrac{1}{x}\leqq\dfrac{1}{k}$ が成り立つ。等号は常には成り立たないから

$y=\dfrac{1}{x}$ は単調に減少する関数であるから,$k\leqq x\leqq k+1$ において,$\dfrac{1}{x}\leqq\dfrac{1}{k}$ が成り立つ。等号は常には成り立たないから
\begin{align*}
&\dint{k}{k+1}\dfrac{1}{x}\;dx<\dint{k}{k+1}\dfrac{1}{k}\;dx \\[4pt]
&\dint{k}{k+1}\dfrac{1}{x}\;dx<\dfrac{1}{k}
\end{align*}
$k=1,~2,~\cdots,~n$ として辺々を加えると,次のようになる。&\dint{k}{k+1}\dfrac{1}{x}\;dx<\dint{k}{k+1}\dfrac{1}{k}\;dx \\[4pt]
&\dint{k}{k+1}\dfrac{1}{x}\;dx<\dfrac{1}{k}
\end{align*}
\begin{align*}
\Sum{k=1}{n}\dint{k}{k+1}\dfrac{1}{x}\;dx<\Sum{k=1}{n}\dfrac{1}{k}
\end{align*}
ここで\Sum{k=1}{n}\dint{k}{k+1}\dfrac{1}{x}\;dx<\Sum{k=1}{n}\dfrac{1}{k}
\end{align*}
\begin{align*}
(左辺)=\dint{1}{n+1}\dfrac{1}{x}\;dx=\log(n+1)
\end{align*}
であるから(左辺)=\dint{1}{n+1}\dfrac{1}{x}\;dx=\log(n+1)
\end{align*}
\begin{align*}
\log(n+1)<1+\dfrac{1}{2}+\dfrac{1}{3}+\cdots+\dfrac{1}{n}
\end{align*}
が成り立つ。\log(n+1)<1+\dfrac{1}{2}+\dfrac{1}{3}+\cdots+\dfrac{1}{n}
\end{align*}
この問題の結果において,$\dlim{n\to\infty}\log(n+1)=\infty$ であることを考えると,
\begin{align*}
&\dlim{n\to\infty}\Sum{k=1}{n}\dfrac{1}{k}=\infty
\end{align*}
であることが分かる。分かりやすく書けば次のようになる。&\dlim{n\to\infty}\Sum{k=1}{n}\dfrac{1}{k}=\infty
\end{align*}
\begin{align*}
1+\dfrac{1}{2}+\dfrac{1}{3}+\cdots=\infty
\end{align*}
1+\dfrac{1}{2}+\dfrac{1}{3}+\cdots=\infty
\end{align*}


















