定積分と不等式の証明の入試問題 第三弾【東北学院大・九州大・津田塾大】

Contents

2007年津田塾大の入試問題の考え方

2007年津田塾大すべての自然数

$n$ に対して，不等式

$\begin{align*} 1+\dfrac{1}{\sqrt2}+\dfrac{1}{\sqrt3}+\cdots+\dfrac{1}{\sqrt{n}}>2\sqrt{n+1}-2 \end{align*}$

が成り立つことを示せ。

ヒロ

問題を見てすぐに「これは面積の大小関係で証明する問題だ」と，今は分かるだろう。それは似たような問題を既に上で解説していたり，タイトルが定積分を含む不等式の証明となっているのが1つの理由だろう。

ヒロ

しかし，実際に試験会場で，本番の入試を受けている状態を考えて欲しい。自然数に関する不等式の証明では，定積分を利用した証明以外に，大きいものから小さいものを引いて正（0以上）になることを証明したり，数学的帰納法で証明するといった様々な証明方法が考えられる。どちらかというと，そういう証明方法を先に考えるのではないだろうか？

ヒロ

証明するべき不等式を見たときに，どのようにして証明方法を決めているのかについては，あまり語られない。大抵はうまく証明できるのを見せられて「なるほど～」と納得している人が相当数いるのではないだろうか？

ヒロ

そうなると，模試などの問題で分からなかったけど，後で解答を見たときに，「定積分で考える問題だったんだ！それなら出来たはず」と意味不明な自信をもつだけで，結局自力で解けないため，また似たような問題で同じように解けない。

ヒロ

実際には証明するべき不等式を見たときに，その不等式の特徴によって，証明方法を決定している。自然数に関する不等式の証明問題では，数学的帰納法が有効である。

何も分からなくても，「『数学的帰納法で証明する』と書いておけ」と冗談のような指導をされることもあるだろう。そんな1行を書いても部分点なんてもらえないだろうと，多くの受験生は思うはず。

しかし，1993年東京工業大の入試でそれは起こった。

「入試数学伝説の良問100」という書籍のコラムとして次の話が掲載されている。
当時，非常に悪い出来だったらしく，このままだと平均点が0点になってしまうが，そんな報告はできない。

その解決策として，「数学的帰納法で証明する」と書けば部分点を与えることを決定したそうだ。その問題の配点は30点なのに，「数学的帰納法で証明する」と書いたら10点与えた。

冗談みたいな話であるが，実話である。これ以降，分からなくても考えた方針だけは書いておいた方が良いという一例となった。

入試数学　伝説の良問100 （ブルーバックス） [ 安田亨 ]

楽天ブックス

Amazon

楽天

Yahoo!ショッピング

ヒロ

受験生にとって1点は非常に重いものである。1点の間にどれほどの受験生が詰まっているかについては，ほとんど知ることはできない。しかし2007年の入試で偶然にも，その一部を知ることができたので紹介しておく。

2007年立命館大と立命館アジア太平洋大の入試で，国語の問題に出題ミスがあった。受験した3582人を全員を正解として採点し直した結果，立命館大で104人，立命館アジア太平洋大で3人が合格最低点を上回ったため追加合格となった。

このことから，たった4点の中に100人以上がいることを偶然にも知ることができた。

「あ～ミスった！」などと軽く「ミス」という人がいるが，そのミスが頻繁に起こるのなら，それは本当にミスなのだろうか？よく考えて欲しい。野球などで頻繁にエラーをする。ピアノで頻繁に弾き間違いをする。頻繁に計算間違いをする。これらを一括りにミスなどと軽く言って，改善策をとらないようでは上達は見込めないのではないだろうか。

頻繁にミスをするなら，それは単に実力不足と言って良いだろう。たかが1点ではあるが，されど1点なのだ。1点を取ることにもっと必死になろう。4点違えば，100人以上抜くことができると思えば1点を大切にするだろう。

ヒロ

脱線したので，話を戻そう。まずは数学的帰納法による証明から。

数学的帰納法による証明

ヒロ

数学的帰納法を利用すると，証明は次のようになる。

すべての自然数

$n$ に対して，不等式

$\begin{align*} 1+\dfrac{1}{\sqrt2}+\dfrac{1}{\sqrt3}+\cdots+\dfrac{1}{\sqrt{n}}>2\sqrt{n+1}-2~\cdots\cdots① \end{align*}$

が成り立つことを数学的帰納法で証明する。

$n=1$ のとき

$\begin{align*} &(左辺)=1 \\[4pt] &(右辺)=2\sqrt{2}-2 \end{align*}$

であり

$\begin{align*} 1-(2\sqrt{2}-2)&=3-2\sqrt{2} \\[4pt] &=\sqrt{9}-\sqrt{8} \\[4pt] &>0 \end{align*}$

となるから，①は成り立つ。

$n=k$ のときに①が成り立つ，すなわち

$\begin{align*} 1+\dfrac{1}{\sqrt2}+\dfrac{1}{\sqrt3}+\cdots+\dfrac{1}{\sqrt{k}}>2\sqrt{k+1}-2 \end{align*}$

が成り立つと仮定する。両辺に

$\dfrac{1}{\sqrt{k+1}}$ を加えると

$\begin{align*} 1+\dfrac{1}{\sqrt2}+\dfrac{1}{\sqrt3}+\cdots+\dfrac{1}{\sqrt{k}}+\dfrac{1}{\sqrt{k+1}}>2\sqrt{k+1}-2+\dfrac{1}{\sqrt{k+1}}~\cdots\cdots② \end{align*}$

となる。ここで

$\begin{align*} &2\sqrt{k+1}-2+\dfrac{1}{\sqrt{k+1}}-(2\sqrt{k+2}-2) \\[4pt] &>\dfrac{1}{\sqrt{k+1}}-2(\sqrt{k+2}-\sqrt{k+1}) \\[4pt] &=\dfrac{1}{\sqrt{k+1}}-\dfrac{2}{\sqrt{k+2}+\sqrt{k+1}} \\[4pt] &=\dfrac{\sqrt{k+2}-\sqrt{k+1}}{\sqrt{k+1}(\sqrt{k+2}+\sqrt{k+1})} \\[4pt] &>0~\cdots\cdots③ \end{align*}$

②，③より

$\begin{align*} 1+\dfrac{1}{\sqrt2}+\dfrac{1}{\sqrt3}+\cdots+\dfrac{1}{\sqrt{k}}+\dfrac{1}{\sqrt{k+1}}>2\sqrt{k+2}-2 \end{align*}$

となり，

$n=k+1$ のときも①が成り立つ。
以上より，すべての自然数

$n$ に対して①が成り立つ。

ヒロ

ちなみに，証明の最後の部分については次のようにしてもよい。

証明の最後の方について，

$\begin{align*} &\dfrac{1}{\sqrt{k+1}}-\dfrac{2}{\sqrt{k+2}+\sqrt{k+1}} \\[4pt] &=\dfrac{2}{\sqrt{k+1}+\sqrt{k+1}}-\dfrac{2}{\sqrt{k+2}+\sqrt{k+1}} \\[4pt] &>0 \end{align*}$

定積分を利用した証明

ヒロ

不等式 $f(n)>\Sum{k=1}{n}g(k)$ において， $f'(x)=g(x)$ のような関係式が成り立つ場合には，定積分を利用する証明方法が有効である。

ヒロ

今回の不等式を見て， $f(x)=\dfrac{1}{\sqrt{x}}$ , $g(x)=\sqrt{x}$ とすると， $g'(x)=\dfrac{1}{2\sqrt{x}}$ となるから， $g'(x)=\dfrac{1}{2}f(x)$ という関係が成り立つ。

ヒロ

このことから， $f(x)$ の定積分を考えることで不等式を証明できるかもしれないと考えよう。

$\dint{}{}\dfrac{1}{\sqrt{x}}\;dx=2\sqrt{x}+C$ であるから，

$\begin{align*} 2\sqrt{n+1}-2=\dint{1}{n+1}\dfrac{1}{\sqrt{x}}\;dx \end{align*}$

となることが分かる。

ヒロ

$y=\dfrac{1}{\sqrt{x}}$ のグラフを描いて， $1\leqq x\leqq n+1$ の部分に着目することで，与えられた不等式を面積の大小関係を考えよう。

$y=\dfrac{1}{\sqrt{x}}$ のグラフは次のようになる。

ヒロ

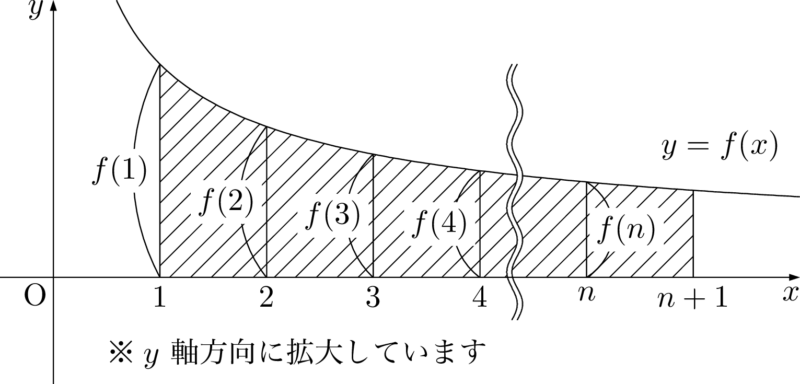
上で計算したように，右辺の $2\sqrt{n+1}-2$ は斜線部分の面積を表している。また，与えられた左辺は右辺より大きいため，斜線部分の面積より大きい面積になるような図形を考えることになる。

ヒロ

今回の問題では，右側に長方形を作ると斜線部分の面積より大きい図形を作ることができると分かる。

【右側に長方形を作った図】

ヒロ

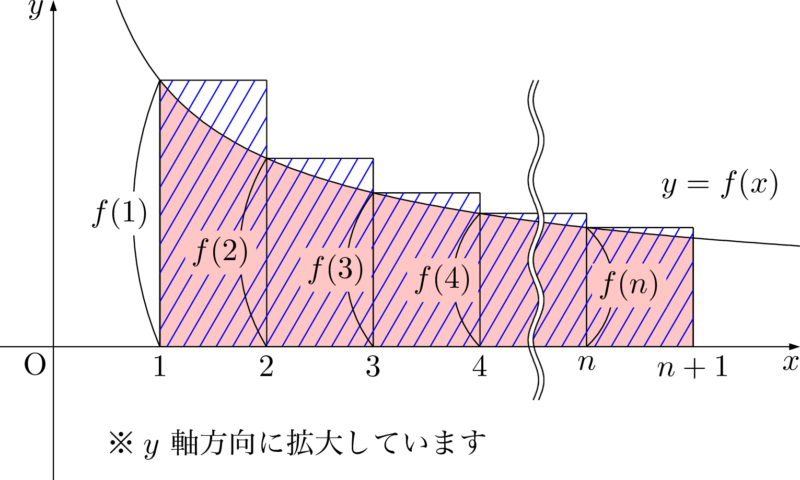
あとは幅が1の区間それぞれに対して証明するだけだね。

関数

$y=\dfrac{1}{\sqrt{x}}$ は単調に減少する関数であるから，

$k$ を自然数とすると，

$k\leqq x\leqq k+1$ において，

$\begin{align*} \dfrac{1}{\sqrt{x}}\leqq\dfrac{1}{\sqrt{k}} \end{align*}$

が成り立つ。常には等号は成り立たないから，次のようになる。

$\begin{align*} &\dint{k}{k+1}\dfrac{1}{\sqrt{x}}\;dx<\dint{k}{k+1}\dfrac{1}{\sqrt{k}}\;dx \\[4pt] &\dint{k}{k+1}\dfrac{1}{\sqrt{x}}\;dx<\dfrac{1}{\sqrt{k}} \end{align*}$

$k=1,~2,~\cdots,~n$ として辺々を加えると

$\begin{align*} \Sum{k=1}{n}\dint{k}{k+1}\dfrac{1}{\sqrt{x}}\;dx<\Sum{k=1}{n}\dfrac{1}{\sqrt{k}} \end{align*}$

となる。ここで

$\begin{align*} \Sum{k=1}{n}\dint{k}{k+1}\dfrac{1}{\sqrt{x}}\;dx&=\dint{1}{n+1}\dfrac{1}{\sqrt{x}}\;dx \\[4pt] &=\tint{2\sqrt{x}}{1}{n+1} \\[4pt] &=2\sqrt{n+1}-2 \end{align*}$

であるから

$\begin{align*} 1+\dfrac{1}{\sqrt2}+\dfrac{1}{\sqrt3}+\cdots+\dfrac{1}{\sqrt{n}}>2\sqrt{n+1}-2 \end{align*}$

が成り立つ。

この問題の結果において，

$\dlim{n\to\infty}(2\sqrt{n+1}-2)=\infty$ であることを考えると，

$\begin{align*} &\dlim{n\to\infty}\Sum{k=1}{n}\dfrac{1}{\sqrt{k}}=\infty \end{align*}$

であることが分かる。分かりやすく書けば次のようになる。

$\begin{align*} 1+\dfrac{1}{\sqrt2}+\dfrac{1}{\sqrt3}+\cdots+\dfrac{1}{\sqrt{n}}+\cdots=\infty \end{align*}$