Contents
3点を通る2次関数を簡単に求める方法の準備

ヒロ
それでは,3点を通る2次関数を簡単に求める方法を説明するよ。

ヒロ
1つ1つ理解する必要があるから,2次関数の求め方について,今日の問題に関係する部分の復習をしていこう。

はい!

ヒロ
まずは次の問題の場合は,求める2次関数をどのようにおく?
補題12点 $(1,0),(-2,0)$ を通る2次関数はどのように表すことができるか?

よくある問題ですね。$y=a(x-1)(x+2)$ とおきます。

ヒロ
そうだね! $a$ の値によって,グラフの形状は変わるね。
【 $y=a(x-1)(x+2)$ のグラフ 】
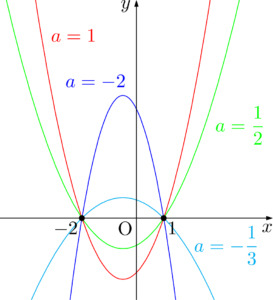
$a$ の値が変わっても,グラフは2点 $(1,0),(-2,0)$ を通る。

ヒロ
では次の問題はどうする?
補題22点 $(1,5),(-2,5)$ を通る2次関数はどのように表すことができるか?

$y$ 座標が2点とも5で同じだけど,これをどうすれば・・・

ヒロ
$y$ 座標が5で同じっていうのには気付いてるよね?

それは分かってるんですけど・・・

ヒロ
補題1では,$y=a(x-1)(x+2)$ とおいたけど,この式を「$x$ に $1$ と $-2$ を代入すると $y=0$ になる式」と捉えよう。

じゃあ,補題2では,「$x$ に $1$ と $-2$ を代入すると $y=5$ になる式」にすれば良いということですね。つまり,$y=a(x-1)(x+2)+5$ ってことですか?

ヒロ
そうだね!$y=a(x-1)(x+2)$ のグラフを $y$ 軸方向に5だけ平行移動したものだと考えても良いよ。
【 $y=a(x-1)(x+2)+5$ のグラフ】
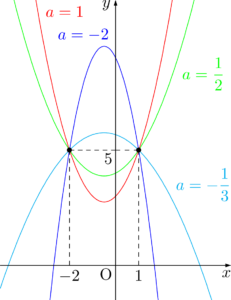
$a$ の値が変わっても,グラフは2点 $(1,5),(-2,5)$ を通る。


















