Contents
3点を通る2次関数を簡単に求める方法

それでは,最初の問題を解いていこう。

はい,お願いします。
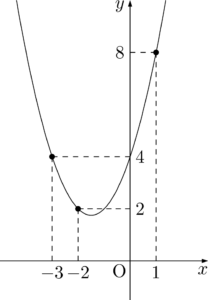
3点 $(1,8),(-2,2),(-3,4)$ を通る2次関数を求めよ。

とりあえず,$y=a(x-1)(x+2)$ を利用しよう。ただし,このままだと $x=1,~-2$ のときに,$y=0$ となってしまうからダメだね。$x=1$ のときには $y=8$ になって,$x=-2$ のときには $y=2$ になってくれるような便利な式があれば良いね。
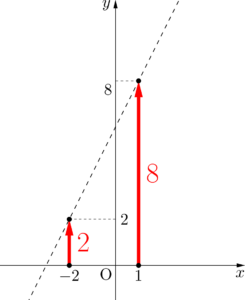

なるほど!2点 $(1,8),(-2,2)$ を通る直線の方程式を考えるんですね!

そうだね!じゃあ,その直線の傾きは?

$\displaystyle \frac{8-2}{1-(-2)}=\frac{6}{3}=2$ だから,傾きは2です。

ということで,一旦 $x=1$ のときに $y=0$ となるように,$y=2(x-1)$ として,実際には $x=1$ のときに $y=8$ だから,$y=2(x-1)+8$ つまり $y=2x+6$ となるね。
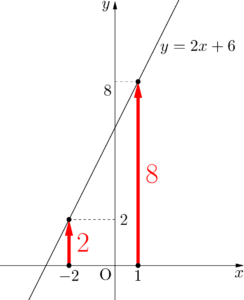

なるほど。他の方法として,傾きが2と分かっているから,一旦 $y=2x$ として,$x=1$ のときに $y=8$ になるように定数項を調整して,$y=2x+6$ としても良いですよね!

そうだね!実際そうやって暗算してる人も多いね。

ということで,2点 $(1,8),(-2,2)$ を通る2次関数は,$y=a(x-1)(x+2)+2x+6$ とおけるね。

なるほど。確かに $x=1$ のときには $y=8$ になって,$x=-2$ のときには $y=2$ になりますね。$2x+6$ が1次式だから,それを $y=a(x-1)(x+2)$ に加えても2次関数のままなんですね。
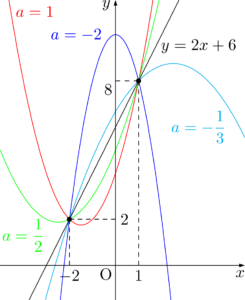
$a$ の値が変わっても,グラフは2点 $(1,5),(-2,5)$ を通る。

確認もバッチリだね。これで1文字だけで表せたんだけど,$a$ はどうやって求めるか分かるよね?

任せて下さい!$x=-3$ と $y=4$ を代入して,$a$ の方程式を解けば良いんですね!

そういうことだね。

でも,これって実際に解答を書くときはどんな風に書けば良いんですか?

次のように書いとけば良いよ。
これが点 $(-3,4)$ を通るから,
&4=a\cdot(-4)\cdot(-1) \\
&4=4a \\
&a=1
\end{align*}
&y=(x-1)(x+2)+2x+6 \\
&y=x^2+3x+4
\end{align*}

分かりました!これで連立方程式を解かなくて良くなりますね!

そうだね。
2次関数の式を求める方法のまとめ

2次関数を求める問題には,様々なタイプがあるけど,それぞれに応じて適切に2次関数を表せるようにしておこう!
- 軸 $x=p$ が与えられたとき
$y={\color{red}{a}}(x-p)^2+{\color{red}{q}}$ - 頂点 $(p,q)$ が与えられたとき
$y={\color{red}{a}}(x-p)^2+q$ - 通る2点 ${\mathrm A}(p,q), {\mathrm B}(r,s)$ が与えられたとき
$y={\color{red}{a}}(x-p)(x-r)+mx+n$
ただし,直線ABの方程式を $y=mx+n$ とする。
※赤文字が未知数となる。



















