Contents
三角関数の最大値と最小値【山梨大】
2018年 山梨大関数 $f(x)=2\cos^2\dfrac{x}{2}+\sin x+3$ の区間 $-\dfrac{\pi}{2}\leqq x\leqq\dfrac{\pi}{2}$ における最大値と最小値を求めよ。また,そのときの $x$ の値を求めよ。
【考え方と解答】
まずは角を統一しよう。$\dfrac{x}{2}$ に揃えると,次数は下がらずサインとコサインが混在することになる。$x$ に揃えるとサインとコサインが混在するが次数が下がるから $x$ に揃えよう。
したがって,$f(x)$ は $x=\dfrac{\pi}{4}$ のとき,最大値 $\sqrt{2}+4$ をとり,$x=-\dfrac{\pi}{2}$ のとき,最小値 $3$ をとる。
まずは角を統一しよう。$\dfrac{x}{2}$ に揃えると,次数は下がらずサインとコサインが混在することになる。$x$ に揃えるとサインとコサインが混在するが次数が下がるから $x$ に揃えよう。
\begin{align*}
f(x)&=2\cos^2\dfrac{x}{2}+\sin x+3 \\[4pt]
&=2\Cdota\dfrac{1+\cos x}{2}+\sin x+3 \\[4pt]
&=\sin x+\cos x+4
\end{align*}
合成することで1つの三角関数で表せるから,最大値と最小値を求めることができる。f(x)&=2\cos^2\dfrac{x}{2}+\sin x+3 \\[4pt]
&=2\Cdota\dfrac{1+\cos x}{2}+\sin x+3 \\[4pt]
&=\sin x+\cos x+4
\end{align*}
\begin{align*}
f(x)=\sqrt{2}\sin\left(x+\dfrac{\pi}{4}\right)+4
\end{align*}
$-\dfrac{\pi}{2}\leqq x\leqq\dfrac{\pi}{2}$ のとき,$-\dfrac{\pi}{4}\leqq x+\dfrac{\pi}{4}\leqq\dfrac{3}{4}\pi$ であるからf(x)=\sqrt{2}\sin\left(x+\dfrac{\pi}{4}\right)+4
\end{align*}
\begin{align*}
-\dfrac{1}{\sqrt{2}}\leqq\sin\left(x+\dfrac{\pi}{4}\right)\leqq1
\end{align*}
よって,-\dfrac{1}{\sqrt{2}}\leqq\sin\left(x+\dfrac{\pi}{4}\right)\leqq1
\end{align*}
\begin{align*}
3\leqq f(x)\leqq\sqrt{2}+4
\end{align*}
$x+\dfrac{\pi}{4}=\dfrac{\pi}{2}$ すなわち $x=\dfrac{\pi}{4}$ のとき,$f(x)$ は最大になる。また $x+\dfrac{\pi}{4}=-\dfrac{\pi}{4}$ すなわち $x=-\dfrac{\pi}{2}$ のtき,$f(x)$ は最小になる。3\leqq f(x)\leqq\sqrt{2}+4
\end{align*}
したがって,$f(x)$ は $x=\dfrac{\pi}{4}$ のとき,最大値 $\sqrt{2}+4$ をとり,$x=-\dfrac{\pi}{2}$ のとき,最小値 $3$ をとる。
三角関数の最大値と最小値【愛知学院大】
2017年 愛知学院大$2\sin x+\cos x$ $\left(0\leqq x\leqq\dfrac{\pi}{2}\right)$ の最大値と最小値を求めなさい。
【考え方と解答】
合成して1つの三角関数に変形して考えよう。
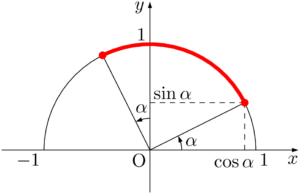
よって,$x+\alpha=\dfrac{\pi}{2}$ すなわち $x=\dfrac{\pi}{2}-\alpha$ のとき最大値 $\sqrt{5}$ をとり,$x=0$ のとき最小値 $1$ をとる。
合成して1つの三角関数に変形して考えよう。
\begin{align*}
2\sin x+\cos x&=\sqrt{5}\sin(x+\alpha)
\end{align*}
ただし,$\alpha$ は2\sin x+\cos x&=\sqrt{5}\sin(x+\alpha)
\end{align*}
\begin{align*}
\cos\alpha=\dfrac{2}{\sqrt{5}},~\sin\alpha=\dfrac{1}{\sqrt{5}}
\end{align*}
をみたす鋭角である。$0\leqq x\leqq\dfrac{\pi}{2}$ のとき,$\alpha\leqq x+\alpha\leqq\dfrac{\pi}{2}+\alpha$ である。\cos\alpha=\dfrac{2}{\sqrt{5}},~\sin\alpha=\dfrac{1}{\sqrt{5}}
\end{align*}

よって,$x+\alpha=\dfrac{\pi}{2}$ すなわち $x=\dfrac{\pi}{2}-\alpha$ のとき最大値 $\sqrt{5}$ をとり,$x=0$ のとき最小値 $1$ をとる。


















