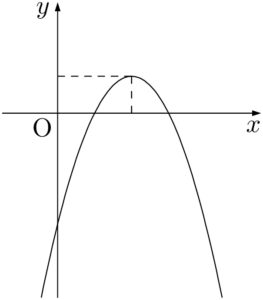
ここでは2次関数のグラフと $x$ 軸の共有点に関する問題を解説します。
2次関数のグラフと $x$ 軸の共有点の $x$ 座標は，2次方程式の解であることもあるため「2次方程式の解の配置問題」と呼ばれます。
2次関数のグラフは放物線であり，解の配置問題では次の4つに着目して考えます。
- 上に凸か下に凸か
- 軸の位置（頂点の $x$ 座標）
- 頂点の $y$ 座標（判別式で代用可能）
- 考える範囲の端点の $y$ 座標
問題で与えられた条件を満たすのは，グラフがどのようになるときかを考えましょう。
慣れないうちはかなり難しく感じますが，諦めなければいつかは解けるようになるでしょう。
また，上に凸か下に凸かを意識していないと，グラフが下に凸の放物線として考えてしまい，符号が逆になってしまうことがあるので注意しましょう。
2次関数のグラフの特徴
ヒロ
ここで，2次関数 $y=ax^2+bx+c$ の $a,~b,~c$ が表しているものを整理しておこう。
ヒロ
例えば，1次関数 $y=ax+b$ の場合は，そのグラフは直線であり，$a$ は直線の傾きを表し，$b$ は切片を表す。
ヒロ
2次関数においても何らかの意味があるはず。
【2次関数 $y=ax^2+bx+c$ の係数の意味】
2次関数のグラフは放物線である。放物線の形状を見ることで，係数 $a,~b,~c$ の符号が分かる。
$a$ の符号によって，放物線が上に凸か下に凸かが決まる。
$a$ が正のときは下に凸であり，$a$ が負のときは上に凸である。
$c$ は放物線の $y$ 切片を表している。
$b$ については，よくあるのは頂点の $x$ 座標 $-\dfrac{b}{2a}$ を考える方法である。
$a$ の符号から $b$ の符号を求めることができる。
2次関数のグラフは放物線である。放物線の形状を見ることで，係数 $a,~b,~c$ の符号が分かる。
$a$ の符号によって，放物線が上に凸か下に凸かが決まる。
$a$ が正のときは下に凸であり，$a$ が負のときは上に凸である。
$c$ は放物線の $y$ 切片を表している。
$b$ については，よくあるのは頂点の $x$ 座標 $-\dfrac{b}{2a}$ を考える方法である。
$a$ の符号から $b$ の符号を求めることができる。
ヒロ
$b,~c$ の符号については，次のように考えて求めることもできる。
【2次関数 $y=ax^2+bx+c$ の $bx+c$ の意味】
$C:y=ax^2+bx+c$ のグラフは放物線であり，$l:y=bx+c$ のグラフは直線である。$C,~l$ の方程式を連立して $y$ を消去すると
つまり，$b,~c$ は放物線 $y=ax^2+bx+c$ 上の点 $(0,~c)$ における接線の傾きと切片を表していることになる。
$C:y=ax^2+bx+c$ のグラフは放物線であり，$l:y=bx+c$ のグラフは直線である。$C,~l$ の方程式を連立して $y$ を消去すると
\begin{align*}
&ax^2+bx+c=bx+c \\[4pt]&ax^2=0 \\[4pt]&x=0（重解）
\end{align*}
$x=0$ が重解であるから，$C$ と $l$ は点 $(0,~c)$ で接することが分かる。&ax^2+bx+c=bx+c \\[4pt]&ax^2=0 \\[4pt]&x=0（重解）
\end{align*}
つまり，$b,~c$ は放物線 $y=ax^2+bx+c$ 上の点 $(0,~c)$ における接線の傾きと切片を表していることになる。
ヒロ
放物線の性質について興味がある人は次の記事も面白く感じるかもしれない。
ヒロ
それでは練習しておこう。
問題2次関数 $y=ax^2+bx+c$ のグラフが次の図のようになっているとき，$a,~b,~c$ の符号を求めよ。
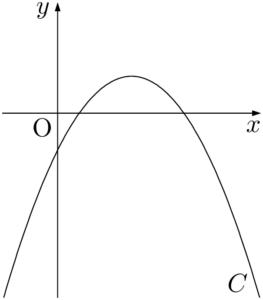
【考え方と解答】
グラフが上に凸であるから，$a$ は負である。
$b,~c$ は次の図のように接線 $l$ を考える。
接線 $l$ は右上がりの直線であるから，$b$ は正である。
$l$ は $y$ 軸と $y$ 座標が負である点と交わるから，$c$ は負である。
グラフが上に凸であるから，$a$ は負である。
$b,~c$ は次の図のように接線 $l$ を考える。
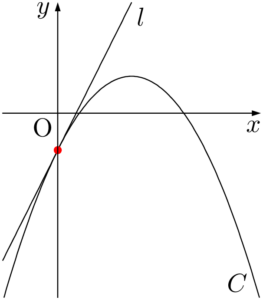
接線 $l$ は右上がりの直線であるから，$b$ は正である。
$l$ は $y$ 軸と $y$ 座標が負である点と交わるから，$c$ は負である。
ヒロ
このように，2次関数のグラフの特徴は頂点と $y$ 切片の2点に現れる。
2次関数のグラフに関する問題
ヒロ
実際に定期テストで出題された問題を解いてみよう。
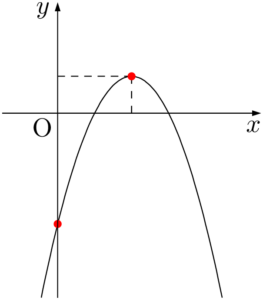
問題 $y=-x^2+(m+2)x+m-6$ のグラフが図のようになるとき，$m$ の値の範囲を求めよ。
【考え方と解答】
赤丸で示した頂点と $y$ 切片に着目して考える。
平方完成すると
頂点が第1象限にあるから，
②より
①’，②’，③より，$2<m<6$
赤丸で示した頂点と $y$ 切片に着目して考える。
平方完成すると
\begin{align*} y=&-x^2+(m+2)x+m-6 \\[4pt] &=-\left(x-\dfrac{m+2}{2}\right)^2+\dfrac{(m+2)^2}{4}+m-6 \\[4pt] &=-\left(x-\dfrac{m+2}{2}\right)^2+\dfrac{1}{4}m^2+2m-5 \end{align*}
頂点の座標は $\left(\dfrac{m+2}{2},~\dfrac{1}{4}m^2+2m-5\right)$ である。頂点が第1象限にあるから，
\begin{align*} \begin{cases} \dfrac{m+2}{2}>0 &~\cdots\cdots① \\[4pt] \dfrac{1}{4}m^2+2m-5 &~\cdots\cdots② \end{cases} \end{align*}
①より，$m>-2~\cdots\cdots①’$②より
\begin{align*} &m^2+8m-20>0 \\[4pt] &(m+10)(m-2)>0 \\[4pt] &m<-10,~2<m~\cdots\cdots②’ \end{align*}
$y$ 切片が負であるから\begin{align*} &m-6<0 \\[4pt] &m<6~\cdots\cdots③ \end{align*}
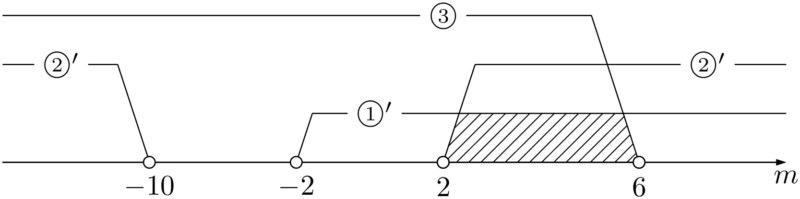
①’，②’，③より，$2<m<6$
ヒロ
②については判別式を $D$ を用いて $D>0$ としても良い。
ヒロ
また，最後の数直線では，大小関係があっていれば，数の間隔は適当で良い。
2次関数と $x$ 軸の共有点に関する問題2
ヒロ
次も定期テストで出題された問題。
問題放物線 $y=x^2-2mx+3m+10$ が $x$ 軸の $-1$ より小さい部分で異なる2点で交わるとき，定数 $m$ の値の範囲を求めよ。
【考え方と解答】
放物線 $y=x^2-2mx+3m+10$ のグラフ $C$ が $x$ 軸の $-1$ より小さい部分で異なる2点で交わるとき，次のようになっている。
ここで，説明のために $C$ と $x$ 軸の共有点の $x$ 座標を $\alpha,~\beta~(\alpha<\beta)$ とおく。 問題文の条件から，青丸で示した2つの解 $\alpha,~\beta$ に着目して
放物線 $y=x^2-2mx+3m+10$ のグラフ $C$ が $x$ 軸の $-1$ より小さい部分で異なる2点で交わるとき，次のようになっている。
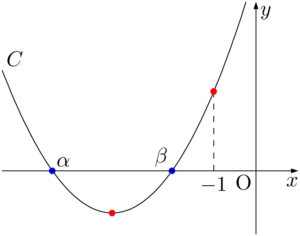
ここで，説明のために $C$ と $x$ 軸の共有点の $x$ 座標を $\alpha,~\beta~(\alpha<\beta)$ とおく。 問題文の条件から，青丸で示した2つの解 $\alpha,~\beta$ に着目して
\begin{align*} \beta<-1 \end{align*}
という不等式を立てて考える人がいるが，解くのに少し苦労するかもしれない。ヒロ
授業で説明されることは少ないだろうから，ここでは解いておく。
【解に着目した解答】
条件をみたすとき，$x^2-2mx+3m+10=0~\cdots\cdots①$ は異なる2つの実数解をもつから，判別式を $D$ とすると $D>0$ で
$m<-2$ のとき，②の両辺は正であるから，2乗すると
\begin{align*} &\dfrac{D}{4}=m^2-(3m+10)>0 \\[4pt] &m^2-3m-10>0 \\[4pt] &(m-5)(m+2)>0 \\[4pt] &m<-2,~5<m \end{align*}
このとき①を解くと\begin{align*} x=m\pm\sqrt{m^2-3m-10} \end{align*}
となり，これらはともに $-1$ より小さいから \begin{align*} &m+\sqrt{m^2-3m-10}<-1 \\[4pt] &\sqrt{m^2-3m-10}<-m-1~\cdots\cdots② \end{align*}
$m>5$ のとき，②の右辺は負であるから②は成り立たない。（②の左辺は正だから）$m<-2$ のとき，②の両辺は正であるから，2乗すると
\begin{align*} &m^2-3m-10<(-m-1)^2 \\[4pt] &m^2-3m-10<m^2+2m+1 \\[4pt] &-5m<11 \\[4pt] &m>-\dfrac{11}{5} \end{align*}
$m<-2$ との共通部分を考えて，求める $m$ の値の範囲は \begin{align*} -\dfrac{11}{5}<m<-2 \end{align*}
ヒロ
解の配置問題では，青丸の解を直接扱わず，赤丸で示した頂点や端点で考えることが多い。
ヒロ
頂点は上下左右の動きを考えて，端点は上下の動きを考えて条件をみたすようにしよう。
【考え方と解答】
$f(x)=x^2-2mx+3m+10$ とおくと，条件をみたすのは
①，②$’$，③$’$より，$-\dfrac{11}{5}<m<-2$
\begin{align*} y&=x^2-2mx+3m+10 \\[4pt] &=(x-m)^2-m^2+3m+10 \end{align*}
より，頂点の座標は $(m,~-m^2+3m+10)$$f(x)=x^2-2mx+3m+10$ とおくと，条件をみたすのは
\begin{align*} \begin{cases} 頂点の~x~座標：m<-1 &~\cdots\cdots① \\[4pt] 頂点の~y~座標：-m^2+3m+10<0 &~\cdots\cdots② \\[4pt] 端点：f(-1)=5m+11>0 &~\cdots\cdots③ \end{cases} \end{align*}
②より\begin{align*} &m^2-3m-10>0 \\[4pt] &(m-5)(m+2)>0 \\[4pt] &m<-2,~5<m ~\cdots\cdots②’ \end{align*}
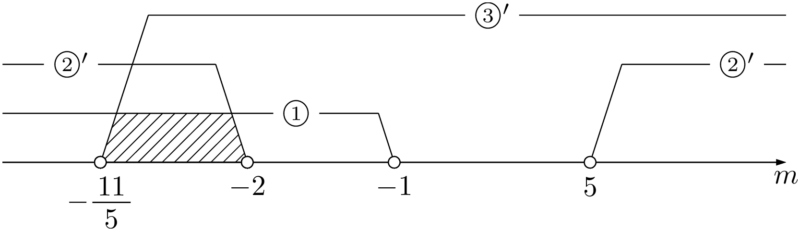
③より，$m>-\dfrac{11}{5} ~\cdots\cdots③’$①，②$’$，③$’$より，$-\dfrac{11}{5}<m<-2$
2次関数と $x$ 軸の共有点に関する問題3
ヒロ
次も定期テストで出題された問題。
問題 関数 $y=x^2+2ax+2a+3$ のグラフを $x$ 軸が次の範囲において異なる2点で交わるとき，定数 $a$ の値の範囲を求めよ。1点は $0<x<1$，他の1点は $2<x<3$
【考え方と解答】
条件をみたすとき，$C:y=x^2+2ax+2a+3$ のグラフは次のようになる。
この問題でも，青丸で示した2つの解（$x=\alpha,~\beta$）を考えるのではなく，赤丸で示した端点の上下の動きを考える。$f(x)=x^2+2ax+2a+3$ とおくと，条件を満たすのは
条件をみたすとき，$C:y=x^2+2ax+2a+3$ のグラフは次のようになる。
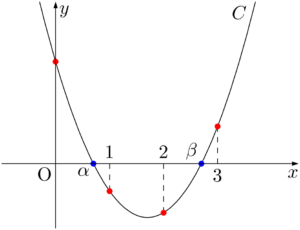
この問題でも，青丸で示した2つの解（$x=\alpha,~\beta$）を考えるのではなく，赤丸で示した端点の上下の動きを考える。$f(x)=x^2+2ax+2a+3$ とおくと，条件を満たすのは
\begin{align*} \begin{cases} f(0)>0 &~\cdots\cdots① \\[4pt] f(1)<0 &~\cdots\cdots② \\[4pt] f(2)<0 &~\cdots\cdots③ \\[4pt] f(3)>0 &~\cdots\cdots④ \end{cases} \end{align*}
①より \begin{align*} &2a+3>0 \\[4pt] &a>-\dfrac{3}{2}~\cdots\cdots①’ \end{align*}
②より \begin{align*} &4a+4<0 \\[4pt] &a<-1~\cdots\cdots②’ \end{align*}
③より \begin{align*} &6a+7<0 \\[4pt] &a<-\dfrac{7}{6}~\cdots\cdots③’ \end{align*}
④より \begin{align*} &8a+12>0 \\[4pt] &a>-\dfrac{3}{2}~\cdots\cdots④’ \end{align*}
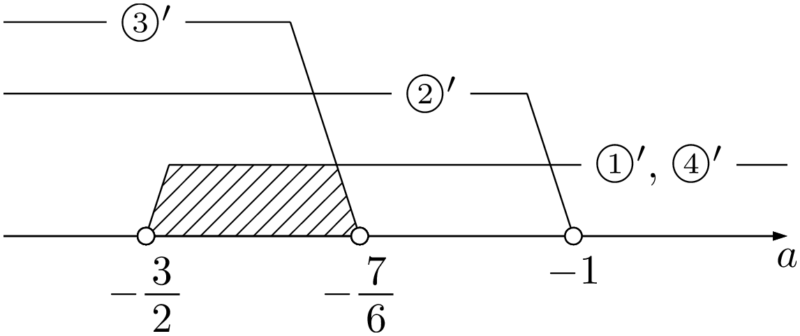
①’～④’より，$-\dfrac{3}{2}<a<-\dfrac{7}{6}$