Contents
- ページ1
- ページ2
- 1 正弦のグラフ
- ページ3
- 1 余弦のグラフ
- ページ4
- 1 正接のグラフ
- ページ5
- 1 三角関数のグラフの対称性
- 2 三角関数のグラフの周期性
三角関数のグラフの対称性

ヒロ
$y=\sin\theta$,$y=\cos\theta$,$y=\tan\theta$ のグラフの対称性について理解しておこう。

ヒロ
そのために,偶関数と奇関数について知っておこう。
偶関数と奇関数関数 $f(x)$ について,$f(-x)=f(x)$ が成り立つものを偶関数といい,$f(-x)=-f(x)$ が成り立つものを奇関数という。偶関数のグラフは $y$ 軸に関して対称であり,奇関数のグラフは原点に関して対称である。

ヒロ
偶関数・奇関数に着目して,基本的な三角関数のグラフの対称性を理解しよう。
【三角関数のグラフの対称性】
$\sin(-\theta)=-\sin\theta$ であるから,$y=\sin\theta$ は奇関数であり,そのグラフは原点に関して対称である。
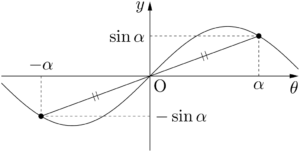
$\cos(-\theta)=\cos\theta$ であるから,$y=\cos\theta$ は偶関数であり,そのグラフは $y$ 軸に関して対称である。
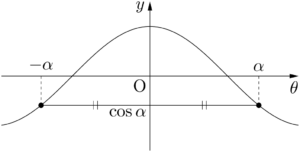
$\tan(-\theta)=-\tan\theta$ であるから,$y=\tan\theta$ は奇関数であり,そのグラフは原点に関して対称である。
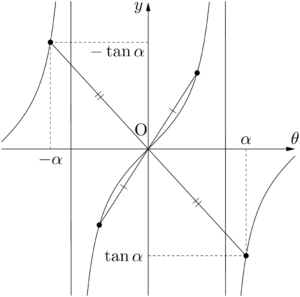
$\sin(-\theta)=-\sin\theta$ であるから,$y=\sin\theta$ は奇関数であり,そのグラフは原点に関して対称である。

$\cos(-\theta)=\cos\theta$ であるから,$y=\cos\theta$ は偶関数であり,そのグラフは $y$ 軸に関して対称である。

$\tan(-\theta)=-\tan\theta$ であるから,$y=\tan\theta$ は奇関数であり,そのグラフは原点に関して対称である。

三角関数のグラフの周期性

ヒロ
三角関数のグラフは,円周上の点と連動する点によって描かれるため,同じことが繰り返されるグラフとなる。

ヒロ
「同じことが一定間隔で繰り返されること」を「周期的」というため,三角関数のグラフは「周期的なグラフ」である。
周期関数とは関数 $f(x)$ において,ある定数 $p$ に対して
周期が複数ある場合は,正の値の最小のものを基本周期という。また,基本周期のことを単に周期ということが多い。
\begin{align*}
f(x+p)=f(x)
\end{align*}
が成り立つとき,$f(x)$ を周期関数といい,定数 $p$ を $f(x)$ の周期という。f(x+p)=f(x)
\end{align*}
周期が複数ある場合は,正の値の最小のものを基本周期という。また,基本周期のことを単に周期ということが多い。

ヒロ
基本的な三角関数の周期を理解しよう。
【三角関数の周期】
$n$ を整数とすると
$n$ を整数とすると
\begin{align*}
&\sin(\theta+2n\pi)=\sin\theta \\[4pt]
&\cos(\theta+2n\pi)=\cos\theta \\[4pt]
&\tan(\theta+n\pi)=\tan\theta
\end{align*}
が成り立つから,$\sin\theta$ と $\cos\theta$ の基本周期はともに $2\pi$ であり,$\tan\theta$ の基本周期は $\pi$ である。&\sin(\theta+2n\pi)=\sin\theta \\[4pt]
&\cos(\theta+2n\pi)=\cos\theta \\[4pt]
&\tan(\theta+n\pi)=\tan\theta
\end{align*}



















