ここでは連立不等式の表す領域について説明します。
大学入試で出題される領域の問題のほとんどは,連立不等式が表す領域を扱っています。
不等式がどの領域を表しているかを正確に把握できるようにしましょう。
Contents
円と放物線を境界線とする領域【東北大】
2016年 東北大連立不等式
\begin{align*}
\begin{cases}
x^2+y^2\leqq1 \\[4pt]
y\geqq x^2-1
\end{cases}
\end{align*}
の表す領域を $D$ とおく。領域 $D$ の概形を図示せよ。\begin{cases}
x^2+y^2\leqq1 \\[4pt]
y\geqq x^2-1
\end{cases}
\end{align*}
【考え方と解答】
領域 $D$ の境界は,円と放物線でそれらの方程式はそれぞれ
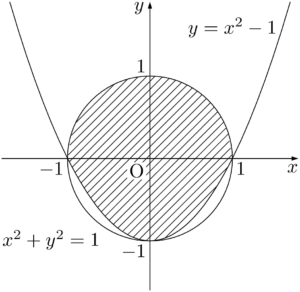
領域 $D$ の境界は,円と放物線でそれらの方程式はそれぞれ
\begin{align*}
&x^2+y^2=1~\cdots\cdots① \\[4pt]
&y=x^2-1~\cdots\cdots②
\end{align*}
である。①,②より $x$ を消去すると&x^2+y^2=1~\cdots\cdots① \\[4pt]
&y=x^2-1~\cdots\cdots②
\end{align*}
\begin{align*}
&(y+1)+y^2=1 \\[4pt]
&y(y+1)=0 \\[4pt]
&y=0,~-1
\end{align*}
$y=0$ のとき,②より&(y+1)+y^2=1 \\[4pt]
&y(y+1)=0 \\[4pt]
&y=0,~-1
\end{align*}
\begin{align*}
&x^2-1=0 \\[4pt]
&x=\pm1
\end{align*}
$y=-1$ のとき,②より&x^2-1=0 \\[4pt]
&x=\pm1
\end{align*}
\begin{align*}
&x^2=0 \\[4pt]
&x=0
\end{align*}
よって,円①と放物線②は共有点を3つもち,それらの座標は $(-1,~0)$,$(1,~0)$,$(0,~-1)$ である。$x^2+y^2\leqq1$ は円①の周および内部を表し,$y\geqq x^2-1$ は放物線②の上側の部分(境界を含む)を表す。2つの領域の共通部分が領域 $D$ であるから,求める領域は下図の斜線部分となる。ただし,境界を含む。&x^2=0 \\[4pt]
&x=0
\end{align*}



















