Contents
三角形の成立条件と領域【学習院大】
2019年 学習院大平面上の点 (x, y) について，次の条件
3辺の長さが 1,~x,~y であるような三角形が存在する。
を満たす点 (x,~y) からなる領域を求め，図示せよ。
3辺の長さが 1,~x,~y であるような三角形が存在する。
を満たす点 (x,~y) からなる領域を求め，図示せよ。
ヒロ
三角形の成立条件については，次の記事を参考にしよう。
【考え方と解答】
3辺の長さが 1,~x,~y である三角形が存在する条件は
3辺の長さが 1,~x,~y である三角形が存在する条件は
\begin{align*} \abs{x-y}<1<x+y \end{align*}
である。x\geqq y のとき \begin{align*} &x-y<1<x+y \\[4pt] &\begin{cases} y>x-1 \\[4pt] y>-x+1 \end{cases} \end{align*}
x\leqq y のとき\begin{align*} &y-x<1<x+y \\[4pt] &\begin{cases} y<x+1 \\[4pt] y>-x+1 \end{cases} \end{align*}
以上より，条件をみたす点 (x,~y) の存在範囲は下図の斜線部分となる。ただし，境界を含まない。直線を境界線とする領域【中京大】
2020年 中京大a\geqq0,~b\geqq0,~c\geqq0，a+b+c=1 のとき，x=a+3b+2c，y=3a+4b+c で表せる点 (x,~y) が存在する範囲を求め，その領域を xy 平面上に図示せよ。
【考え方と解答】
3つの等式から，a,~b,~c を x,~y で表すことができる。a\geqq0,~b\geqq0,~c\geqq0 に代入することで，x,~y の不等式を3つ作ることができる。あとは，その3つの不等式が表す領域を図示すれば終わりだね。
a+b+c=1 より，c=1-a-b
x=a+3b+2c，y=3a+4b+c に代入して
求める領域は，\sankaku{PQR} の周および内部で，下図の斜線部分である。ただし，境界を含む。
3つの等式から，a,~b,~c を x,~y で表すことができる。a\geqq0,~b\geqq0,~c\geqq0 に代入することで，x,~y の不等式を3つ作ることができる。あとは，その3つの不等式が表す領域を図示すれば終わりだね。
a+b+c=1 より，c=1-a-b
x=a+3b+2c，y=3a+4b+c に代入して
\begin{align*} x&=a+3b+2(1-a-b) \\[4pt] &=-a+b+2 \cdots\cdots① \\[4pt] y&=3a+4b+(1-a-b) \\[4pt] &=2a+3b+1 \cdots\cdots② \end{align*}
①\times3-② より\begin{align*} &3x-y=-5a+5 \\[4pt] &a=\dfrac{1}{5}(-3x+y+5)~\cdots\cdots③ \end{align*}
①\times2+② より\begin{align*} &2x+y=5b+5 \\[4pt] &b=\dfrac{1}{5}(2x+y-5)~\cdots\cdots④ \end{align*}
③を a\geqq0 に代入して\begin{align*} -3x+y-5\geqq0~\cdots\cdots⑤ \end{align*}
④を b\geqq0 に代入して\begin{align*} 2x+y-5\geqq0~\cdots\cdots⑥ \end{align*}
c\geqq0 より，1-a-b\geqq0 であるから，③と④を代入して\begin{align*} &1-\dfrac{1}{5}(-3x+y+5)-\dfrac{1}{5}(2x+y-5)\geqq0 \\[4pt] &x-2y+5\geqq0~\cdots\cdots⑦ \end{align*}
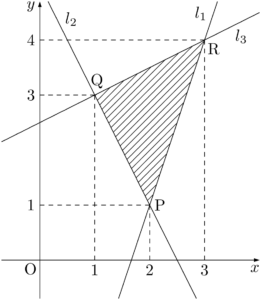
⑤，⑥，⑦の境界線 -3x+y-5=0，2x+y-5=0，x-2y+5=0 をそれぞれ l_1,~l_2,~l_3 とし，l_1 と l_2 の交点をP(2,~1)，l_2 と l_3 の交点をQ(1,~3)，l_3 と l_1 の交点をR(3,~4) とする。求める領域は，\sankaku{PQR} の周および内部で，下図の斜線部分である。ただし，境界を含む。