Contents
不等式の表す領域に関する問題【東京電機大】
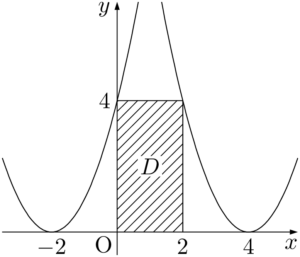
2020年 東京電機大不等式 $0\leqq x\leqq2$,$0\leqq y\leqq4$ で表される領域を $D$ とする。さらに実数 $t$ に対して,不等式 $y\geqq(x-t)^2$ で表される領域を $E_t$ とする。$D$ と $E_t$ が共有点をもつような $t$ の値の範囲を求めよ。
【考え方と解答】
領域 $D$ は下図の斜線部分の長方形の周および内部である。

領域 $E_t$ は放物線 $y=(x-t)^2$ の上側(境界を含む)の部分である。
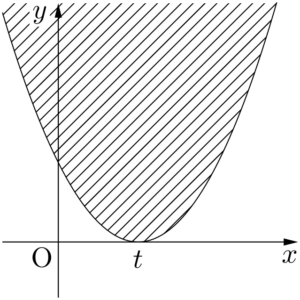
$t$ の値を変えると,放物線は $x$ 軸に接しながら動くことを考えて,$D$ と $E_t$ が共有点をもつような $t$ の値の範囲を求めよう。
上のアニメーションから,放物線 $y=(x-t)^2$ が点 $(0,~4)$ を通るときと点 $(2,~4)$ を通るときが,2つの領域 $D,~E_t$ が共有点をギリギリもつときであることが分かる。共有点をもつかどうかの境界となる $t$ の値を求めよう。
$y=(x-t)^2$ が点 $(0,~4)$ を通るとき,
以上より,$D$ と $E_t$ が共有点をもつための $t$ の値の範囲は,$-2\leqq t\leqq4$ である。
領域 $D$ は下図の斜線部分の長方形の周および内部である。

領域 $E_t$ は放物線 $y=(x-t)^2$ の上側(境界を含む)の部分である。

$t$ の値を変えると,放物線は $x$ 軸に接しながら動くことを考えて,$D$ と $E_t$ が共有点をもつような $t$ の値の範囲を求めよう。
上のアニメーションから,放物線 $y=(x-t)^2$ が点 $(0,~4)$ を通るときと点 $(2,~4)$ を通るときが,2つの領域 $D,~E_t$ が共有点をギリギリもつときであることが分かる。共有点をもつかどうかの境界となる $t$ の値を求めよう。
$y=(x-t)^2$ が点 $(0,~4)$ を通るとき,
\begin{align*}
&(-t)^2=4 \\[4pt]
&t=\pm2
\end{align*}
$y=(x-t)^2$ が点 $(2,~4)$ を通るとき,&(-t)^2=4 \\[4pt]
&t=\pm2
\end{align*}
\begin{align*}
&(2-t)^2=4 \\[4pt]
&2-t=\pm2 \\[4pt]
&t=0,~4
\end{align*}
それぞれのときに対応する $t$ の値が2つ出てきたが,グラフを見ることで,どちらの $t$ が知りたい値かを判断しよう。&(2-t)^2=4 \\[4pt]
&2-t=\pm2 \\[4pt]
&t=0,~4
\end{align*}

以上より,$D$ と $E_t$ が共有点をもつための $t$ の値の範囲は,$-2\leqq t\leqq4$ である。


















