Contents
円を境界線とする領域

ヒロ
円 $(x-a)^2+(y-b)^2=r^2$ を $C$ とする。
円を境界線とする領域
- 不等式 $(x-a)^2+(y-b)^2>r^2$ の表す領域は,円 $C$ の外部である。ただし,境界を含まない。
- 不等式 $(x-a)^2+(y-b)^2<r^2$ の表す領域は,円 $C$ の内部である。ただし,境界を含まない。
不等式の表す領域とは

ヒロ
「領域」とはどのようなものかを理解しておこう。
不等式の表す領域不等式をみたす点全体の集合を,その不等式の表す領域という。

ヒロ
例として「$y>\dfrac{1}{2}x+1$ の表す領域」を考える。
【$y>\dfrac{1}{2}x+1~\cdots\cdots(*)$ の表す領域】
$y=\dfrac{1}{2}x+1$ は傾き $\dfrac{1}{2}$,切片1の直線 $l$ を表すから,ある点の座標が $y=\dfrac{1}{2}x+1$ をみたすとき,その点は直線 $l$ 上にある。例えば,点 $(2,~2)$ は $2=\dfrac{1}{2}\Cdot2+1$ となるから,直線 $l$ 上にある。
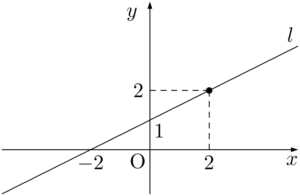
点 $(2,~2)$ と $x$ 座標が等しく $y$ 座標が大きい点 $(2,~3)$ は,$3>\dfrac{1}{2}\Cdot2+1$ が成り立つから,点 $(2,~3)$ は不等式(*)を満たす点である。
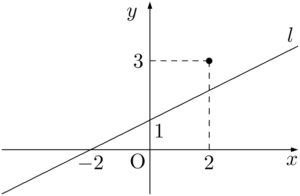
$x$ 座標を2に固定して考えると,$y$ 座標が2より大きい点は,すべて不等式(*)をみたすことが分かる。
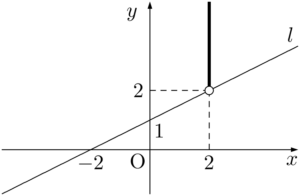
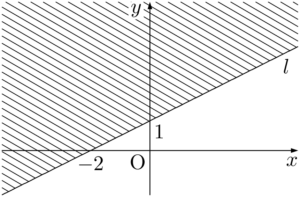
$x$ 座標を動かすことで,不等式 $y>\dfrac{1}{2}x+1$ が表す領域は直線 $y=\dfrac{1}{2}x+1$ の上側(境界を含まない)であることが分かる。図示すると,下図の斜線部分となる。

ヒロ
境界を含まないときに,斜線を境界線に付けないように描いているものもあるが,本ブログでは,常に斜線を境界線に付けて描く。


















