Contents
不等式の表す領域に関する問題【東北学院大】
2018年 東北学院大不等式 $x^2+y^2\leqq3$ の表す領域 $A$,不等式 $\abs{x-\sqrt{3}}+\sqrt{3}\abs{y}<\sqrt{3}$ で表す領域を $B$ とする。以下の問いに答えよ。
(1) $A$ を図示せよ。
(2) $B$ を図示せよ。
(1) $A$ を図示せよ。
(2) $B$ を図示せよ。
【(1)の考え方と解答】
領域 $A$ は円 $x^2+y^2=3$ の周および内部であるから,次の斜線部分(境界を含む)となる。

領域 $A$ は円 $x^2+y^2=3$ の周および内部であるから,次の斜線部分(境界を含む)となる。

(2) $B$ を図示せよ。
【(2)の考え方と解答】
2つの絶対値の中身の符号で場合分けをしよう。
①より
(ii) $x\geqq\sqrt{3},~y\leqq0$ のとき
①より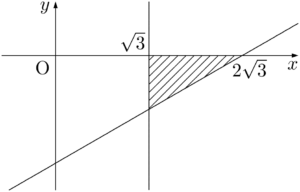
(iii) $x\leqq\sqrt{3},~y\geqq0$ のとき
①より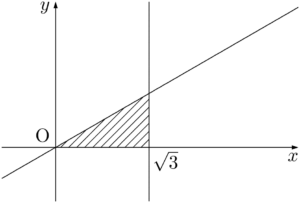
(iv) $x\leqq\sqrt{3},~y\leqq0$ のとき
①より
(i)~(iv)より,領域 $B$ は下図の斜線部分(境界を含まない)となる。

2つの絶対値の中身の符号で場合分けをしよう。
\begin{align*} \abs{x-\sqrt{3}}+\sqrt{3}\abs{y}<\sqrt{3}~\cdots\cdots① \end{align*}
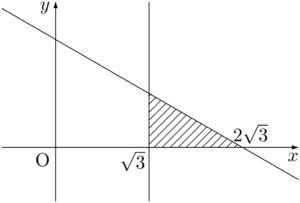
とする。 (i) $x\geqq\sqrt{3},~y\geqq0$ のとき①より
\begin{align*} &x-\sqrt{3}+\sqrt{3}y<\sqrt{3} \\[4pt] &x+\sqrt{3}y<2\sqrt{3} \end{align*}
1つずつ図示する必要はないが,(i)の領域は下図の斜線部分となる。
(ii) $x\geqq\sqrt{3},~y\leqq0$ のとき
①より
\begin{align*} &x-\sqrt{3}-\sqrt{3}y<\sqrt{3} \\[4pt] &x-\sqrt{3}y<2\sqrt{3} \end{align*}

(iii) $x\leqq\sqrt{3},~y\geqq0$ のとき
①より
\begin{align*} &-(x-\sqrt{3})+\sqrt{3}y<\sqrt{3} \\[4pt] &x-\sqrt{3}y>0
\end{align*}
\end{align*}

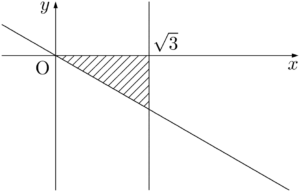
(iv) $x\leqq\sqrt{3},~y\leqq0$ のとき
①より
\begin{align*}
&-(x-\sqrt{3})-\sqrt{3}y<\sqrt{3} \\[4pt] &x+\sqrt{3}y>0
\end{align*}
&-(x-\sqrt{3})-\sqrt{3}y<\sqrt{3} \\[4pt] &x+\sqrt{3}y>0
\end{align*}

(i)~(iv)より,領域 $B$ は下図の斜線部分(境界を含まない)となる。



















