Contents
円と直線で囲まれる領域と2次式の最大・最小【関西学院大】
2020年 関西学院大$xy$ 平面において,連立不等式
点 $(x,~y)$ が領域 $D$ を動くとき,$x^2+y^2-10x-10y$ の最大値は $\myhako$ であり,最小値は $\myhako$ である。
\begin{align*}
x\geqq0,~y\geqq0,~3x+2y\geqq6,~x^2+y^2+2x+2y-34\leqq0
\end{align*}
が表す領域を $D$ とする。x\geqq0,~y\geqq0,~3x+2y\geqq6,~x^2+y^2+2x+2y-34\leqq0
\end{align*}
点 $(x,~y)$ が領域 $D$ を動くとき,$x^2+y^2-10x-10y$ の最大値は $\myhako$ であり,最小値は $\myhako$ である。
【考え方と解答】
この問題で考えるのは,$x^2+y^2-10x-10y$ の最大値と最小値であるが,$x^2+y^2-10x-10y=k$ とおくと,円の方程式のように見えるだろう。変形してみると
また,別の捉え方として,
それでは領域 $D$ を図示して考えよう。領域 $D$ の境界線は座標軸と直線 $3x+2y=6$ と円 $x^2+y^2+2x+2y-34=0$ である。円の方程式は
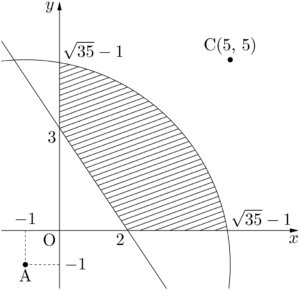
以上より,領域 $D$ は下図の斜線部分(境界を含む)となる。
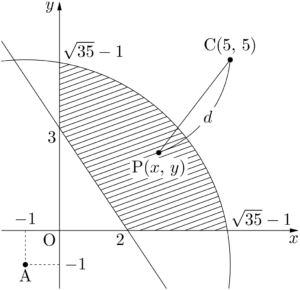
領域 $D$ 内の点P$(x,~y)$ と点C$(5,~5)$ との距離を $d$ とすると,$k=d^2-50$ より,$d$ が最大のとき $k$ が最大となり,$d$ が最小のとき $k$ が最小となる。$d$ が最大や最小になるのは,点Pがどの位置にあるときかを考える。
その際,CPの長さが変わらないように,領域 $D$ 内で点Pを動かすと点Pは点Cを中心とする円弧を描く。逆に言うと,下図の赤色の円弧上で点Pを動かしても,CPの長さは変わらないということである。
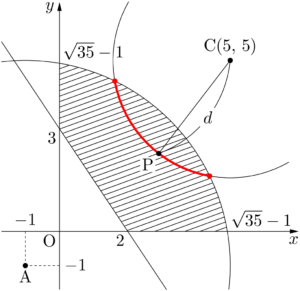
$d$ が最小になるのは,点Cを中心とする半径 $d$ の円と点Aを中心とする半径6の円が外接するときである。$d$ が最大になるのは,点Pが $(2,~0)$ か $(0,~3)$ と一致するときであるが,3点A,O,Cが直線 $y=x$ 上に並んでいることを考えると,点Pが $(2,~0)$ と一致するときに $d$ が最大となることが分かる。これについては,それぞれの距離を計算で求めて確認しても良い。$d$ が最大になる点PをP$_1$ とし,$d$ が最小になる点PをP$_2$ とする。

まず $k$ の最大値を求める。CP$_1$ の長さは
直線ACの傾きが1で,2点の $x$ 座標の差が6であるから,CAの長さは $6\sqrt{2}$ である。したがって,
この問題で考えるのは,$x^2+y^2-10x-10y$ の最大値と最小値であるが,$x^2+y^2-10x-10y=k$ とおくと,円の方程式のように見えるだろう。変形してみると
\begin{align*}
(x-5)^2+(y-5)^2=k+50~\cdots\cdots①
\end{align*}
となるから,$k+50$ が正のとき,①は点C$(5,~5)$ を中心とする半径 $\sqrt{k+50}$ の円を表す。$k+50=0$ のとき,①は1点 $(5,~5)$ を表す。(x-5)^2+(y-5)^2=k+50~\cdots\cdots①
\end{align*}
また,別の捉え方として,
\begin{align*}
k=(x-5)^2+(y-5)^2-50
\end{align*}
と変形すると,$k$ は点 $(5,~5)$ と点P$(x,~y)$ との距離 $d$ の2乗から50を引いたものと考えることができる。k=(x-5)^2+(y-5)^2-50
\end{align*}
それでは領域 $D$ を図示して考えよう。領域 $D$ の境界線は座標軸と直線 $3x+2y=6$ と円 $x^2+y^2+2x+2y-34=0$ である。円の方程式は
\begin{align*}
(x+1)^2+(y+1)^2=36
\end{align*}
と変形できるから,点A$(-1,~-1)$ を中心とする半径6の円である。(x+1)^2+(y+1)^2=36
\end{align*}
以上より,領域 $D$ は下図の斜線部分(境界を含む)となる。

領域 $D$ 内の点P$(x,~y)$ と点C$(5,~5)$ との距離を $d$ とすると,$k=d^2-50$ より,$d$ が最大のとき $k$ が最大となり,$d$ が最小のとき $k$ が最小となる。$d$ が最大や最小になるのは,点Pがどの位置にあるときかを考える。

その際,CPの長さが変わらないように,領域 $D$ 内で点Pを動かすと点Pは点Cを中心とする円弧を描く。逆に言うと,下図の赤色の円弧上で点Pを動かしても,CPの長さは変わらないということである。

$d$ が最小になるのは,点Cを中心とする半径 $d$ の円と点Aを中心とする半径6の円が外接するときである。$d$ が最大になるのは,点Pが $(2,~0)$ か $(0,~3)$ と一致するときであるが,3点A,O,Cが直線 $y=x$ 上に並んでいることを考えると,点Pが $(2,~0)$ と一致するときに $d$ が最大となることが分かる。これについては,それぞれの距離を計算で求めて確認しても良い。$d$ が最大になる点PをP$_1$ とし,$d$ が最小になる点PをP$_2$ とする。

まず $k$ の最大値を求める。CP$_1$ の長さは
\begin{align*}
\text{CP}_1&=\sqrt{(5-2)^2+5^2}=\sqrt{34}
\end{align*}
であるから,$k$ の最大値は\text{CP}_1&=\sqrt{(5-2)^2+5^2}=\sqrt{34}
\end{align*}
\begin{align*}
k&=(\sqrt{34})^2-50=-16
\end{align*}
次に $k$ の最小値を求める。k&=(\sqrt{34})^2-50=-16
\end{align*}
直線ACの傾きが1で,2点の $x$ 座標の差が6であるから,CAの長さは $6\sqrt{2}$ である。したがって,
\begin{align*}
\text{CP}_2&=\text{AC}-\text{AP}_2 \\[4pt]
&=6\sqrt{2}-6
\end{align*}
となるから,$k$ の最小値は\text{CP}_2&=\text{AC}-\text{AP}_2 \\[4pt]
&=6\sqrt{2}-6
\end{align*}
\begin{align*}
k&=(6\sqrt{2}-6)^2-50 \\[4pt]
&=36(3-2\sqrt{2})-50 \\[4pt]
&=58-72\sqrt{2}
\end{align*}
k&=(6\sqrt{2}-6)^2-50 \\[4pt]
&=36(3-2\sqrt{2})-50 \\[4pt]
&=58-72\sqrt{2}
\end{align*}


















