Contents
円と直線で囲まれる領域と最大・最小【学習院大】
2020年 学習院大連立不等式
点P$(x,~y)$ が領域 $D$ を動くとき,$2y-x$ の最大値および最小値を求めよ。
\begin{align*}
x+2y\geqq2,~x^2+y^2\leqq2x
\end{align*}
の表す領域を $D$ とする。x+2y\geqq2,~x^2+y^2\leqq2x
\end{align*}
点P$(x,~y)$ が領域 $D$ を動くとき,$2y-x$ の最大値および最小値を求めよ。
【考え方と解答】
$2y-x=k$ とおくと,これは直線を表す方程式であることが分かるから,領域 $D$ を描いて考えよう。
直線 $x+2y=2~\cdots\cdots①$ と円 $x^2+y^2=2x~\cdots\cdots②$ の共有点を求める。
①より $x=-2y+2$
②に代入すると
したがって,領域 $D$ は下図の斜線部分(境界を含む)となる。
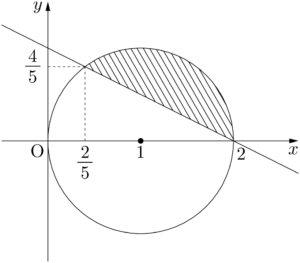
$2y-x=k$ とおくと,$y=\dfrac{1}{2}x+\dfrac{k}{2}$ となるから,グラフは傾き $\dfrac{1}{2}$,切片 $\dfrac{k}{2}$ の直線 $l$ である。$k$ が最大になるのは切片が最大になるときであり,$k$ が最小になるのは切片が最小になるときである。
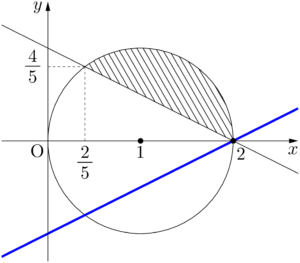
よって,直線 $l$ が点 $(2,~0)$ を通るとき,$k$ は最小になり,最小値は
直線 $l$ が点 $\left(\dfrac{2}{5},~\dfrac{4}{5}\right)$ を通るとき,$k$ の値は
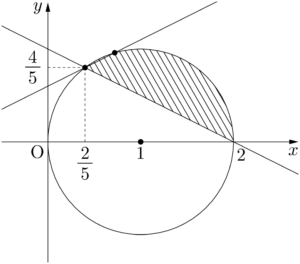
したがって,$k$ が最大になるのは,直線 $l$ と円 $C$ が第1象限で接するときである。直線 $l$ と円 $C$ の中心との距離が1であるから
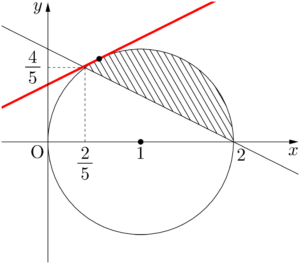
円の中心 $(1,~0)$ を通り,直線 $l$ に垂直な直線 $m$ の方程式は
二式から $y$ を消去すると
よって,接点の座標は $\left(\dfrac{5-\sqrt{5}}{5},~\dfrac{2\sqrt{5}}{5}\right)$
したがって,$2y-x$ は,$(x,~y)=\left(\dfrac{5-\sqrt{5}}{5},~\dfrac{2\sqrt{5}}{5}\right)$ のとき,最大値 $\sqrt{5}-1$ をとり,$(x,~y)=(2,~0)$ のとき,最小値 $-2$ をとる。
$2y-x=k$ とおくと,これは直線を表す方程式であることが分かるから,領域 $D$ を描いて考えよう。
直線 $x+2y=2~\cdots\cdots①$ と円 $x^2+y^2=2x~\cdots\cdots②$ の共有点を求める。
①より $x=-2y+2$
②に代入すると
\begin{align*}
&(-2y+2)^2+y^2=2(-2y+2) \\[4pt]
&5y^2-4y=0 \\[4pt]
&y(5y-4)=0 \\[4pt]
&y=0,~\dfrac{4}{5}
\end{align*}
よって,直線①と円②は2点 $(2,~0)$,$\left(\dfrac{2}{5},~\dfrac{4}{5}\right)$ で交わる。②は $(x-1)^2+y^2=1$ と変形できるから,円②は点 $(1,~0)$ を中心とする半径1の円 $C$ である。&(-2y+2)^2+y^2=2(-2y+2) \\[4pt]
&5y^2-4y=0 \\[4pt]
&y(5y-4)=0 \\[4pt]
&y=0,~\dfrac{4}{5}
\end{align*}
したがって,領域 $D$ は下図の斜線部分(境界を含む)となる。

$2y-x=k$ とおくと,$y=\dfrac{1}{2}x+\dfrac{k}{2}$ となるから,グラフは傾き $\dfrac{1}{2}$,切片 $\dfrac{k}{2}$ の直線 $l$ である。$k$ が最大になるのは切片が最大になるときであり,$k$ が最小になるのは切片が最小になるときである。

よって,直線 $l$ が点 $(2,~0)$ を通るとき,$k$ は最小になり,最小値は
\begin{align*}
k=2\Cdota0-2=-2
\end{align*}
次に $k$ の最大値を求める。直線 $l$ を平行移動して考えると,$k$ が最大になるのは,$l$ が点 $\left(\dfrac{2}{5},~\dfrac{4}{5}\right)$ を通るときか円 $C$ に接するときのいずれかである。どちらの場合が,$l$ が領域 $D$ とギリギリ共有点をもつときかを調べる。k=2\Cdota0-2=-2
\end{align*}
直線 $l$ が点 $\left(\dfrac{2}{5},~\dfrac{4}{5}\right)$ を通るとき,$k$ の値は
\begin{align*}
k=2\Cdota\dfrac{4}{5}-\dfrac{2}{5}=\dfrac{6}{5}
\end{align*}
であるから,$l$ の方程式はk=2\Cdota\dfrac{4}{5}-\dfrac{2}{5}=\dfrac{6}{5}
\end{align*}
\begin{align*}
&2y-x=\dfrac{6}{5} \\[4pt]
&x-2y+\dfrac{6}{5}=0
\end{align*}
となる。このとき,円 $C$ の中心 $(1,~0)$ との距離を $d$ とすると&2y-x=\dfrac{6}{5} \\[4pt]
&x-2y+\dfrac{6}{5}=0
\end{align*}
\begin{align*}
d&=\dfrac{\abs{1+\dfrac{6}{5}}}{\sqrt{5}}=\dfrac{11}{5\sqrt{5}}
\end{align*}
となる。$11^2=121$,$(5\sqrt{5})^2=125$ より,$d<=1$ であることが分かるから,$l$ は $C$ と2点で交わる。d&=\dfrac{\abs{1+\dfrac{6}{5}}}{\sqrt{5}}=\dfrac{11}{5\sqrt{5}}
\end{align*}

したがって,$k$ が最大になるのは,直線 $l$ と円 $C$ が第1象限で接するときである。直線 $l$ と円 $C$ の中心との距離が1であるから
\begin{align*}
&\dfrac{\abs{k+1}}{\sqrt{5}}=1 \\[4pt]
&k+1=\pm\sqrt{5} \\[4pt]
&k=-1\pm\sqrt{5}
\end{align*}
$l$ と $C$ が第1象限で接するのは,$k>0$ のときであるから,$k=-1+\sqrt{5}$ のときである。&\dfrac{\abs{k+1}}{\sqrt{5}}=1 \\[4pt]
&k+1=\pm\sqrt{5} \\[4pt]
&k=-1\pm\sqrt{5}
\end{align*}

円の中心 $(1,~0)$ を通り,直線 $l$ に垂直な直線 $m$ の方程式は
\begin{align*}
&y=-2(x-1) \\[4pt]
&y=-2x+2
\end{align*}
である。$l$ と $C$ の接点は,$l:2y-x=-1+\sqrt{5}$ と $m$ の交点である。&y=-2(x-1) \\[4pt]
&y=-2x+2
\end{align*}
二式から $y$ を消去すると
\begin{align*}
&2(-2x+2)-x=-1+\sqrt{5} \\[4pt]
&5x=5-\sqrt{5} \\[4pt]
&x=\dfrac{5-\sqrt{5}}{5}
\end{align*}
このとき,$y=\dfrac{2\sqrt{5}}{5}$&2(-2x+2)-x=-1+\sqrt{5} \\[4pt]
&5x=5-\sqrt{5} \\[4pt]
&x=\dfrac{5-\sqrt{5}}{5}
\end{align*}
よって,接点の座標は $\left(\dfrac{5-\sqrt{5}}{5},~\dfrac{2\sqrt{5}}{5}\right)$
したがって,$2y-x$ は,$(x,~y)=\left(\dfrac{5-\sqrt{5}}{5},~\dfrac{2\sqrt{5}}{5}\right)$ のとき,最大値 $\sqrt{5}-1$ をとり,$(x,~y)=(2,~0)$ のとき,最小値 $-2$ をとる。


















