Contents
直線で囲まれる領域と最大・最小【日本大】
2020年 日本大連立不等式
\begin{align*}
\begin{cases}
y\leqq-\dfrac{1}{5}x+3, \\[4pt]
y\geqq x-2, \\[4pt]
x\geqq0, \\[4pt]
y\geqq-\dfrac{2}{3}x+2
\end{cases}
\end{align*}
により囲まれる図形を $D$ で表す。$(x,~y)$ を $D$ の点とするとき,$x+3y$ の最小値は $\myhako$ であり,最大値は $\myhako$ である。\begin{cases}
y\leqq-\dfrac{1}{5}x+3, \\[4pt]
y\geqq x-2, \\[4pt]
x\geqq0, \\[4pt]
y\geqq-\dfrac{2}{3}x+2
\end{cases}
\end{align*}

ヒロ
「まず,連立不等式で表された図形 $D$ を描こう。」と言いたいところであるが,「その後の方針」は頭の中にあるかどうかが重要である。

ヒロ
もし,図形 $D$ を描いたあと,どのように考えて $x+3y$ の最大値と最小値を求めるのかさっぱり分かっていなければ意味がない。

ヒロ
記述式試験なら部分点をもらえるだろうが,今回のような空欄補充では答えが合っているかどうかで得点できるかどうかが決まる。

ヒロ
したがって,図形 $D$ を描いた後の方針から説明することにする。
$x+3y$ は $x$ と $y$ の値が変化すると値が変わる式であり,2つの文字を同時に色々な値に変えて,その式の最大値や最小値を求めるなんてことはかなり難しいし面倒なことである。
例えば,$(x,~y)=(1,~2)$ のとき,$x+3y=7$ となるが,値を変えて $(x,~y)=(4,~1)$ のときを調べても $x+3y=7$ となり,$x,~y$ の値を変えているのに $x+3y$ の値が変わらないこともある。
$(x,~y)$ の組を基準に $x+3y$ の値の変化を考えるのではなく,$x+3y$ の値を決めて,その値に対応する $(x,~y)$ の組を考える。
例えば $x+3y=7$ となる $(x,~y)$ の値の組を考えてみる。具体的な値の組を考えようとしたときに,$x+3y=7$ のグラフを考える人が多いだろう。その時点で,$x+3y=7$ は直線を表すことに気付き,直線上の点であれば,常に $x+3y$ の値が7になることが分かる。
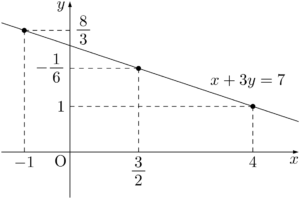
直線 $x+3y=7$ が図形 $D$ と共有点をもっていれば,そのすべての共有点 $(x,~y)$ に対して $x+3y=7$ が成り立つ。逆に直線 $x+3y=7$ が図形 $D$ と共有点をもっていなければ,$x+3y=7$ となる $(x,~y)$ は存在しないことになる。
したがって,$x+3y=k$ とおいて,直線 $x+3y=k$ が図形 $D$ と共有点をもつような最大の $k$ と最小の $k$ を探すことで $x+3y$ の最大値と最小値を求めることができる。$x+3y=k$ を変形すると $y=-\dfrac{1}{3}x+\dfrac{k}{3}$ となるから,傾き $-\dfrac{1}{3}$ で切片 $\dfrac{k}{3}$ の直線である。この直線は傾きが $-\dfrac{1}{3}$ で一定であるから,$k$ の値を変化させると,上下に平行移動する。
切片が $\dfrac{k}{3}$ であることから,切片が最大となるときに $k$ が最大,すなわち,$x+3y$ が最大となる。また,切片が最小となるときに $x+3y$ が最小となることが分かる。
【考え方と解答】
図形 $D$ は下図の斜線部分(境界を含む)である。
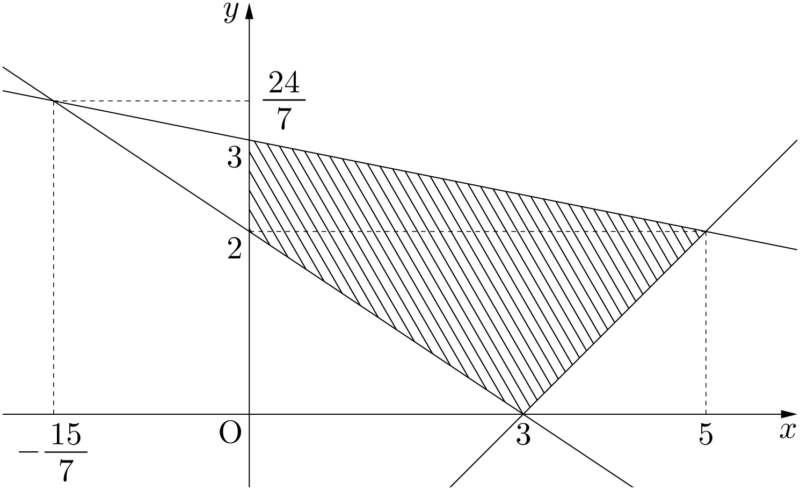
くどいかもしれないが,例として考えた $x+3y=7$ のときを考える。直線 $x+3y=7$ 上の点で,図形 $D$ 内の部分を赤色で描くと次のようになる。当然のことであるが,赤い線分上の点 $(x,~y)$ では,必ず $x+3y$ の値が7になる。
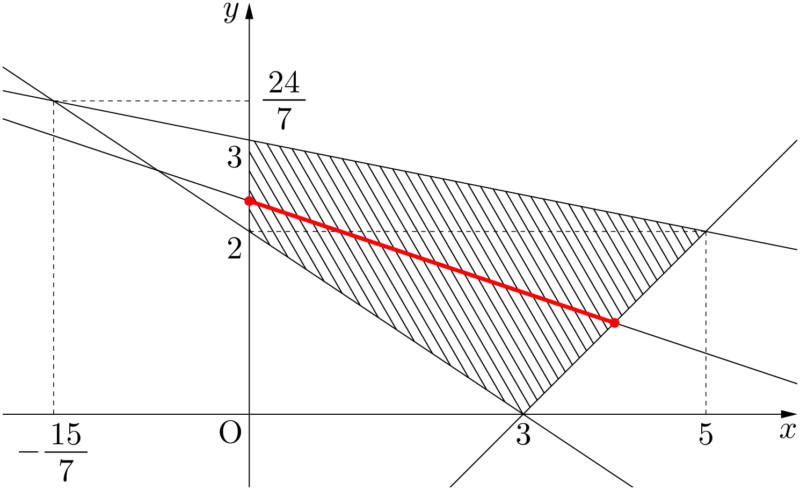
グラフを見れば $k$ の値を7より大きい値をとることができそうである。そこで文字を利用して考える。
$x+3y=k$ とおくと,$y=-\dfrac{1}{3}x+\dfrac{k}{3}$ となるから,グラフは傾き $-\dfrac{1}{3}$ で切片 $\dfrac{k}{3}$ の直線 $l$ である。$k$ の値を変えることで,直線 $l$ が上下に動くから,図形 $D$ と共有点をもつ範囲で上下に動かして切片が最大になるときと最小になるときを求める。
直線 $l$ が点 $(3,~0)$ を通るとき $k$ は最小で,このとき
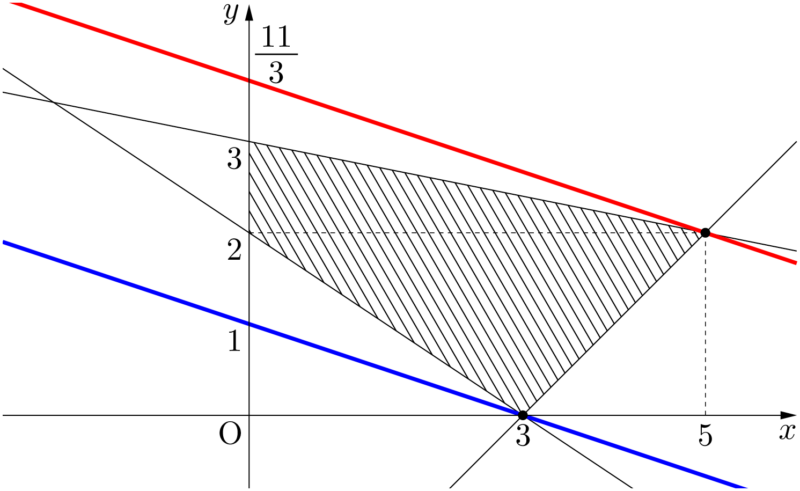
図形 $D$ は下図の斜線部分(境界を含む)である。

くどいかもしれないが,例として考えた $x+3y=7$ のときを考える。直線 $x+3y=7$ 上の点で,図形 $D$ 内の部分を赤色で描くと次のようになる。当然のことであるが,赤い線分上の点 $(x,~y)$ では,必ず $x+3y$ の値が7になる。

グラフを見れば $k$ の値を7より大きい値をとることができそうである。そこで文字を利用して考える。
$x+3y=k$ とおくと,$y=-\dfrac{1}{3}x+\dfrac{k}{3}$ となるから,グラフは傾き $-\dfrac{1}{3}$ で切片 $\dfrac{k}{3}$ の直線 $l$ である。$k$ の値を変えることで,直線 $l$ が上下に動くから,図形 $D$ と共有点をもつ範囲で上下に動かして切片が最大になるときと最小になるときを求める。
直線 $l$ が点 $(3,~0)$ を通るとき $k$ は最小で,このとき
\begin{align*}
k&=3+3\Cdota0=3
\end{align*}
直線 $l$ が点 $(5,~2)$ を通るとき $k$ は最大で,このときk&=3+3\Cdota0=3
\end{align*}
\begin{align*}
k&=5+3\Cdota2=11
\end{align*}
k&=5+3\Cdota2=11
\end{align*}



















