前回に引き続き,三角比を利用して空間図形の問題を解く方法について説明します。
空間図形の問題では,体積を求める問題が多く出題されるため,様々な問題を解いて慣れておくことが重要です。
平面図形の問題として考える部分と,空間図形の問題として考える部分をうまく切り替えられるようになりましょう。
三角錐と三角比の問題

ヒロ
空間図形の基礎力を鍛える問題が茨城大で出題されている。
2019年 茨城大$x$ を正の実数とする。四面体OABCにおいて,
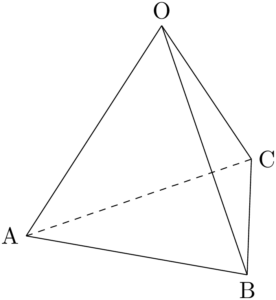
(1) $x$ のとり得る値の範囲を求めよ。
(2) 四面体OABCの体積を $x$ を用いて表せ。
(3) $x$ が(1)の範囲を動くとき,四面体OABCの体積の最大値を求めよ。
\begin{align*}
\text{OA}=\text{OB}=\text{OC}=\text{AC}=\text{BC}=1,~\text{AB}=2x
\end{align*}
とするとき,以下の各問に答えよ。\text{OA}=\text{OB}=\text{OC}=\text{AC}=\text{BC}=1,~\text{AB}=2x
\end{align*}

(1) $x$ のとり得る値の範囲を求めよ。
(2) 四面体OABCの体積を $x$ を用いて表せ。
(3) $x$ が(1)の範囲を動くとき,四面体OABCの体積の最大値を求めよ。

ヒロ
(1)は三角形の成立条件を考えよう。

ヒロ
一言で「三角形の成立条件を考えよう。」と言っても,あまりよく考えずに解くと間違えてしまう。
【(1)の誤答例】
$\sankaku{OAB}$ と $\sankaku{CAB}$ のどちらに着目しても次のようになる。
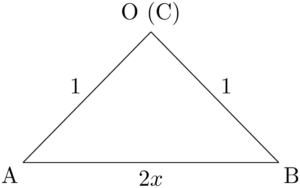
したがって,三角形の成立条件より

したがって,三角形の成立条件より
\begin{align*} &\abs{1-1}<2x<1+1 \\[4pt] &0<x<1 \end{align*}

ヒロ
一見,何も問題がないように見えるが,辺OC上の任意の点をPとしたときに,$\sankaku{PAB}$ に対しても三角形の成立条件を満たす必要がある。

ヒロ
PAやPBの長さはOAやOBより短くなるため,$x$ の値の取り方次第では,$\sankaku{PAB}$ が存在しなくなる。

ヒロ
正しい解答は次のようになる。
【(1)の考え方と解答】
与えられた辺の長さから $\sankaku{OAC}$ と $\sankaku{OBC}$ はともに1辺が1の正三角形であることが分かる。ABの長さが変化するとき,2平面OAC, OBCのなす角が変化する。
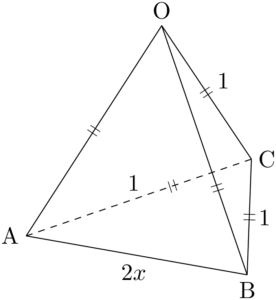
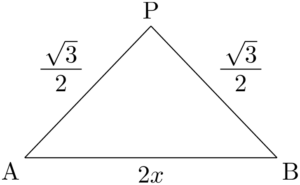

辺OCに垂直で,2点A, Bを通る平面とOCとの交点をPとすると,$\kaku{APB}$ が2平面OAC, OBCのなす角である。

$\sankaku{OAC}$ と $\sankaku{OBC}$ が正三角形であるから,PはOCの中点である。したがって
\begin{align*} \text{PA}=\text{PB}=\dfrac{\sqrt{3}}{2} \end{align*}
となる。
条件をみたす四面体OABCが存在するのは,$\sankaku{PAB}$ が存在するときである。よって,$\sankaku{PAB}$ の成立条件より
\begin{align*} &\dfrac{\sqrt{3}}{2}-\dfrac{\sqrt{3}}{2}<2x<\dfrac{\sqrt{3}}{2}+\dfrac{\sqrt{3}}{2} \\[4pt] &0<x<\dfrac{\sqrt{3}}{2} \end{align*}
(2) 四面体OABCの体積を $x$ を用いて表せ。
【(2)の考え方と解答】
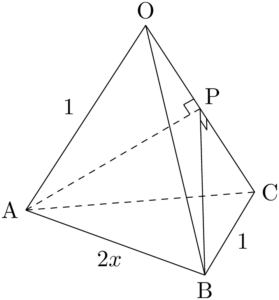
四面体OABCの体積を求めるために,底面と高さを考えよう。もし,$\sankaku{ABC}$ を底面とすると,高さは点Oから底面ABCに下ろした垂線の長さとなる。この考え方だと,やってみれば分かるが,計算が少し面倒になる。今回は(1)でOCに垂直な平面ABPを考えているから,これをうまく利用しよう。
つまり,四面体OABCを平面ABPで切って2つの四面体に分割すると,それぞれの四面体の高さがOP, PCとなる。したがって,四面体OABCの体積を $V$ とすると
\begin{align*} V&=\text{四面体OABP}+\text{四面体PABC} \\[4pt] &=\dfrac{1}{3}\sankaku{ABP}\Cdota\text{OP}+\dfrac{1}{3}\sankaku{ABP}\Cdota\text{PC} \\[4pt] &=\dfrac{1}{3}\sankaku{ABP}\Cdota\text{OC} \end{align*}
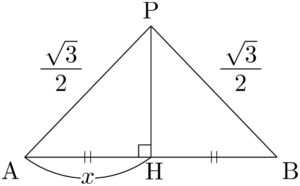
$\sankaku{ABP}$ が二等辺三角形であるから,点Pから辺ABに垂線PHを下ろすとHはABの中点となる。
よって
\begin{align*} \text{PH}&=\sqrt{\left(\dfrac{\sqrt{3}}{2}\right)^2-x^2} \\[4pt] &=\dfrac{1}{2}\sqrt{3-4x^2} \end{align*}
となるから \begin{align*} \sankaku{ABP}&=\dfrac{1}{2}\Cdota\text{AB}\Cdota\text{PH} \\[4pt] &=\dfrac{1}{2}\Cdota2x\Cdota\dfrac{1}{2}\sqrt{3-4x^2} \\[4pt] &=\dfrac{1}{2}x\sqrt{3-4x^2} \end{align*}
したがって \begin{align*} V&=\dfrac{1}{3}\Cdota\dfrac{1}{2}x\sqrt{3-4x^2}\Cdota1 \\[4pt] &=\dfrac{1}{6}x\sqrt{3-4x^2} \end{align*}
(3) $x$ が(1)の範囲を動くとき,四面体OABCの体積の最大値を求めよ。
【(3)の考え方と解答】
(2)で求めた $V$ の最大値を考える方法としては,数学IIIの微分を利用する方法がある。しかし,この問題は,数学IIIが出題範囲ではない大学(学部)で出題されることもあるので,工夫の仕方を知っておくと良いだろう。$x$ を根号内に入れると
\begin{align*} V&=\dfrac{1}{6}\sqrt{3x^2-4x^4} \end{align*}
となり,根号内が複二次式となるため,2次関数の最大値を求める問題として考えることができる。\begin{align*} V&=\dfrac{1}{6}\sqrt{-4\left(x^2-\dfrac{3}{8}\right)^2+\dfrac{9}{16}} \end{align*}
$0<x^2<\dfrac{3}{4}$ より,$x^2=\dfrac{3}{8}$ のとき,$V$ は最大となる。すなわち,$x=\dfrac{\sqrt{3}}{2\sqrt{2}}=\dfrac{\sqrt{6}}{4}$ のとき,$V$ は最大値 $\dfrac{1}{8}$ をとる。正四面体と三角比の問題

ヒロ
三角錐(四面体)の中でも,4つの面すべてが正三角形であるとき,正四面体という。

ヒロ
正四面体は入試でよく出題されるので,練習しておこう。
2017年 大阪市立大・文系1辺の長さが2の正四面体OABCの辺OA上にA以外の点Pをとる。点Pから平面ABCへ垂線をおろし,その垂線と平面ABCの交点をHとする。$\text{PA}=t$ とするとき,次の問いに答えよ。
(1) 三角形HBCの面積 $S$ を $t$ を用いて表せ。
(2) 線分PHの長さを $t$ を用いて表せ。
(3) 四面体PHBCの体積 $V$ が最大となるような $t$ と,そのときの $V$ の値を求めよ。
(1) 三角形HBCの面積 $S$ を $t$ を用いて表せ。
(2) 線分PHの長さを $t$ を用いて表せ。
(3) 四面体PHBCの体積 $V$ が最大となるような $t$ と,そのときの $V$ の値を求めよ。
【(1)の考え方と解答】
図を描くと次のようになる。
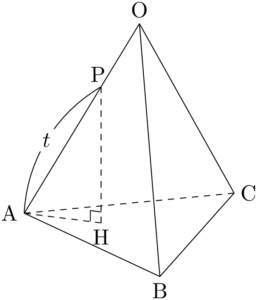
$\text{OA}=\text{OB}=\text{OC}$ であるから,点Oから平面ABCに下した垂線の足は $\sankaku{ABC}$ の外心となる。$\sankaku{ABC}$ の外心をGとすると,点Hは直線AG上にあり,直線AGと辺BCの交点はBCの中点Mとなる。
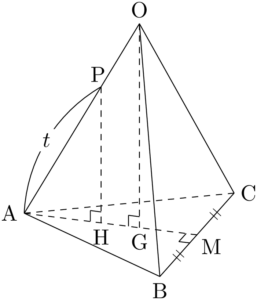
したがって,$\sankaku{HBC}$ の面積を求めるために,$\text{HM}$ の長さを求める。そのために $\text{AM}:\text{HM}$ を調べる。$\text{OA}=3$ であるから,
図を描くと次のようになる。

$\text{OA}=\text{OB}=\text{OC}$ であるから,点Oから平面ABCに下した垂線の足は $\sankaku{ABC}$ の外心となる。$\sankaku{ABC}$ の外心をGとすると,点Hは直線AG上にあり,直線AGと辺BCの交点はBCの中点Mとなる。

したがって,$\sankaku{HBC}$ の面積を求めるために,$\text{HM}$ の長さを求める。そのために $\text{AM}:\text{HM}$ を調べる。$\text{OA}=3$ であるから,
\begin{align*}
\text{AH}:\text{AG}&=\text{AP}:\text{AO} \\[4pt]&=t:2
\end{align*}
また,点Gは $\sankaku{ABC}$ の重心であるから\text{AH}:\text{AG}&=\text{AP}:\text{AO} \\[4pt]&=t:2
\end{align*}
\begin{align*}
\text{AG}:\text{GM}=2:1
\end{align*}
したがって\text{AG}:\text{GM}=2:1
\end{align*}
\begin{align*}
&\text{AH}:\text{HG}:\text{GM}=t:(2-t):1 \\[4pt]&\text{AM}:\text{HM}=3:(3-t)
\end{align*}
$\sankaku{ABM}$ は $1:2:\sqrt{3}$ の直角三角形であるから,$\text{AM}=\sqrt{3}$ となり,&\text{AH}:\text{HG}:\text{GM}=t:(2-t):1 \\[4pt]&\text{AM}:\text{HM}=3:(3-t)
\end{align*}
\begin{align*}
\text{HM}&=\dfrac{3-t}{3}\text{AM} \\[4pt]&=\dfrac{(3-t)\sqrt{3}}{3}
\end{align*}
よって $\sankaku{HBC}$ の面積 $S$ は\text{HM}&=\dfrac{3-t}{3}\text{AM} \\[4pt]&=\dfrac{(3-t)\sqrt{3}}{3}
\end{align*}
\begin{align*}
S&=\dfrac{1}{2}\text{BC}\Cdota\text{HM} \\[4pt]&=\dfrac{1}{2}\Cdota2\Cdota\dfrac{(3-t)\sqrt{3}}{3} \\[4pt]&=\sqrt{3}-\dfrac{\sqrt{3}}{3}t
\end{align*}
S&=\dfrac{1}{2}\text{BC}\Cdota\text{HM} \\[4pt]&=\dfrac{1}{2}\Cdota2\Cdota\dfrac{(3-t)\sqrt{3}}{3} \\[4pt]&=\sqrt{3}-\dfrac{\sqrt{3}}{3}t
\end{align*}
(2) 線分PHの長さを $t$ を用いて表せ。
【(2)の考え方と解答】
$\sankaku{APH}$ に着目して三平方の定理を利用しよう。
$\text{AH}:\text{AM}=t:3$ より
$\sankaku{APH}$ に着目して三平方の定理を利用しよう。
$\text{AH}:\text{AM}=t:3$ より
\begin{align*}
\text{AH}=\dfrac{t}{3}\text{AM}=\dfrac{\sqrt{3}t}{3}
\end{align*}
であるから\text{AH}=\dfrac{t}{3}\text{AM}=\dfrac{\sqrt{3}t}{3}
\end{align*}
\begin{align*}
\text{PH}&=\sqrt{\text{AP}^2-\text{AH}^2} \\[4pt]&=\sqrt{t^2-\dfrac{t^2}{3}} \\[4pt]&=\sqrt{\dfrac{2}{3}t^2}=\dfrac{\sqrt{6}}{3}t
\end{align*}
\text{PH}&=\sqrt{\text{AP}^2-\text{AH}^2} \\[4pt]&=\sqrt{t^2-\dfrac{t^2}{3}} \\[4pt]&=\sqrt{\dfrac{2}{3}t^2}=\dfrac{\sqrt{6}}{3}t
\end{align*}
(3) 四面体PHBCの体積 $V$ が最大となるような $t$ と,そのときの $V$ の値を求めよ。
【(3)の考え方と解答】
$\sankaku{HBC}$ を底面,$\text{PH}$ を高さとみて体積を求めよう。
$\sankaku{HBC}$ を底面,$\text{PH}$ を高さとみて体積を求めよう。
\begin{align*} V&=\dfrac{1}{3}\sankaku{HBC}\Cdota\text{PH} \\[4pt] &=\dfrac{1}{3}\Cdota\dfrac{\sqrt{3}(3-t)}{3}\Cdota\dfrac{\sqrt{2}}{\sqrt{3}}t \\[4pt] &=\dfrac{\sqrt{2}}{9}(3-t)t \\[4pt] &=\dfrac{\sqrt{2}}{9}\left\{-\left(t-\dfrac{3}{2}\right)^2+\dfrac{9}{4}\right\} \end{align*}
$0<t\leqq2$ より $t=\dfrac{3}{2}$ のとき $V$ は最大値 $\dfrac{\sqrt{2}}{4}$ をとる。正四面体の体積

ヒロ
正四面体の体積については,よく出題されるため,公式として覚えている人もいる。
正四面体の体積1辺の長さが $a$ の正四面体OABCの体積を $V$ とする。

三角形ABCの面積を $S$ とすると

三角形ABCの面積を $S$ とすると
\begin{align*}
S=\dfrac{\sqrt{3}}{4}a^2
\end{align*}
であり,点Oから底面ABCに垂線OHを下ろし,OHの長さを $h$ とするとS=\dfrac{\sqrt{3}}{4}a^2
\end{align*}
\begin{align*}
h=\dfrac{\sqrt{6}}{3}a
\end{align*}
となるから,h=\dfrac{\sqrt{6}}{3}a
\end{align*}
\begin{align*}
V&=\dfrac{1}{3}Sh \\[4pt]&=\dfrac{1}{3}\Cdota\dfrac{\sqrt{3}}{4}a^2\Cdota\dfrac{\sqrt{6}}{3}a \\[4pt]&=\dfrac{\sqrt{2}}{12}a^3
\end{align*}
V&=\dfrac{1}{3}Sh \\[4pt]&=\dfrac{1}{3}\Cdota\dfrac{\sqrt{3}}{4}a^2\Cdota\dfrac{\sqrt{6}}{3}a \\[4pt]&=\dfrac{\sqrt{2}}{12}a^3
\end{align*}