Contents
2つの放物線で囲まれる領域と分数式の最大値【酪農学園大】
2020年 酪農学園大連立不等式
(1) 領域 $A$ を図示せよ。
(2) 点 $(x,~y)$ が領域 $A$ を動くとき,$\dfrac{2y-16}{x-5}$ の最大値とそのときの $(x,~y)$ を求めよ。
\begin{align*}
y\geqq x^2-1,~y\leqq-x^2+4x+5
\end{align*}
の表す領域を $A$ とする。次の各問いに答えよ。y\geqq x^2-1,~y\leqq-x^2+4x+5
\end{align*}
(1) 領域 $A$ を図示せよ。
(2) 点 $(x,~y)$ が領域 $A$ を動くとき,$\dfrac{2y-16}{x-5}$ の最大値とそのときの $(x,~y)$ を求めよ。
【(1)の考え方と解答】
領域 $A$ の境界線は,次の2つの放物線である。
したがって,求める領域 $A$ は下図の斜線部分(境界を含む)である。
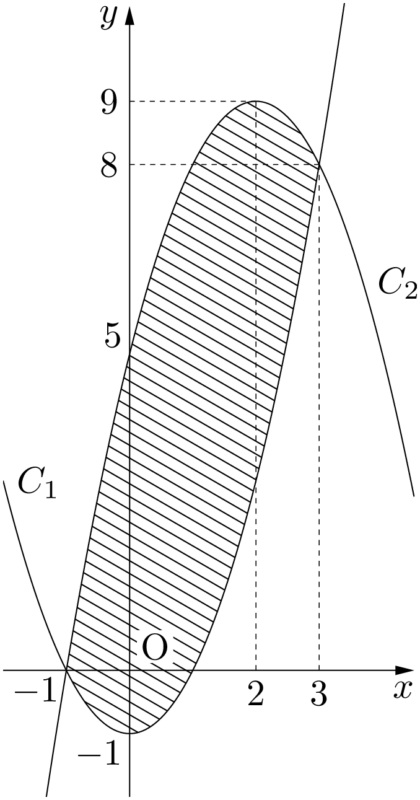
領域 $A$ の境界線は,次の2つの放物線である。
\begin{align*}
&C_1:y=x^2-1 \\[4pt]
&C_2:y=-x^2+4x+5
\end{align*}
2つの放物線の交点を求める。二式より $y$ を消去すると&C_1:y=x^2-1 \\[4pt]
&C_2:y=-x^2+4x+5
\end{align*}
\begin{align*}
&2x^2-4x-6=0 \\[4pt]
&x^2-2x-3=0 \\[4pt]
&(x-3)(x+1)=0 \\[4pt]
&x=-1,~3
\end{align*}
よって,2つの放物線は2点 $(-1,~0)$,$(3,~8)$ で交わる。&2x^2-4x-6=0 \\[4pt]
&x^2-2x-3=0 \\[4pt]
&(x-3)(x+1)=0 \\[4pt]
&x=-1,~3
\end{align*}
したがって,求める領域 $A$ は下図の斜線部分(境界を含む)である。

(2) 点 $(x,~y)$ が領域 $A$ を動くとき,$\dfrac{2y-16}{x-5}$ の最大値とそのときの $(x,~y)$ を求めよ。
【(2)の考え方と解答】
まず,分母が $x-5$ より,$x\neq5$ である。
$\dfrac{2y-16}{x-5}=k$ とおくと,
\begin{align*}
&2y-16=k(x-5) \\[4pt]
&y=\dfrac{k}{2}(x-5)+8
\end{align*}
となるから,これは点A$(5,~8)$ を通り,傾き $\dfrac{k}{2}$ の直線であり,$l$ とする。しかし,$x\neq5$ であるから,実際には点Aを通ることはなく,除かなければならない。
&2y-16=k(x-5) \\[4pt]
&y=\dfrac{k}{2}(x-5)+8
\end{align*}
$k$ が最大になるのは,傾きが最大になるときであり,直線 $l$ が $C_1$ と接するときである。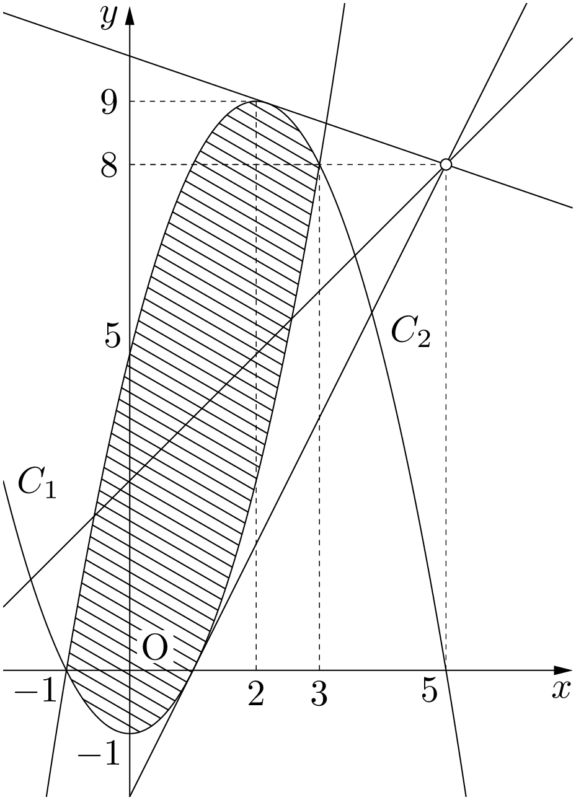
$l,~C_1$ の方程式から $y$ を消去して
\begin{align*}
&x^2-1=\dfrac{k}{2}(x-5)+8 \\[4pt]
&2x^2-kx+5k-18=0
\end{align*}
判別式を $D_1$ とすると $D_1=0$ であるから&x^2-1=\dfrac{k}{2}(x-5)+8 \\[4pt]
&2x^2-kx+5k-18=0
\end{align*}
\begin{align*}
&D_1=k^2-8(5k-18)=0 \\[4pt]
&k^2-40k+144=0 \\[4pt]
&(k-4)(k-36)=0 \\[4pt]
&k=4,~36
\end{align*}
接点の $x$ 座標は $\dfrac{k}{4}$ であり,$-1\leqq x\leqq2$ をみたすのは $k=4$ のときである。このとき,接点の座標は $(1,~0)$ である。&D_1=k^2-8(5k-18)=0 \\[4pt]
&k^2-40k+144=0 \\[4pt]
&(k-4)(k-36)=0 \\[4pt]
&k=4,~36
\end{align*}
graphs-of-inequalities-and-max-and-min-part2-06.png
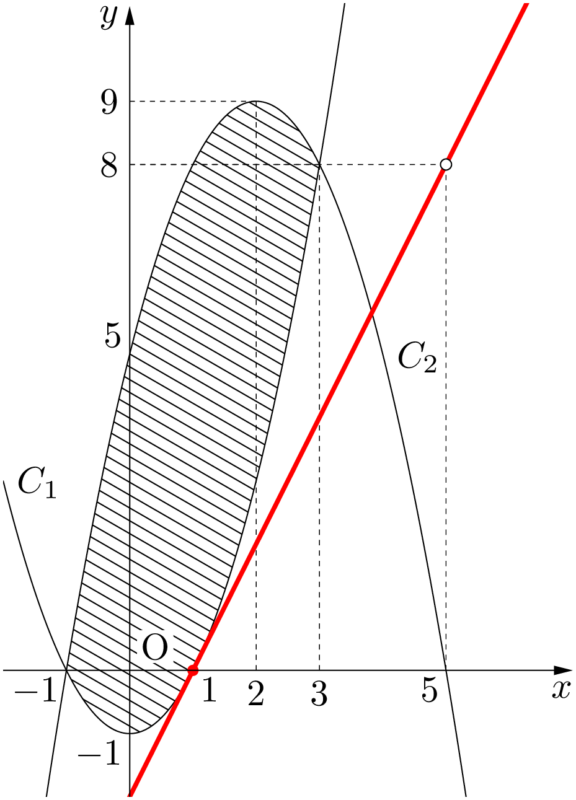
よって,$(x,~y)=(1,~0)$ のとき,$\dfrac{2y-16}{x-5}$ は最大値4をとる。


















