「すべての放物線は相似である」ということを一度は聞いたことがあっても,あまり納得していない人は多いのではないでしょうか?
この記事では,三角形の相似を扱うことで,相似の位置とはどういう意味か,相似の中心とは何かというレベルから説明しています。
この記事を読むことで,すべての放物線が相似であることに納得できるでしょう。
Contents
相似の位置と相似の中心とは

ヒロ
まずは三角形の相似を考えることで,相似の位置と相似の中心について説明していく。
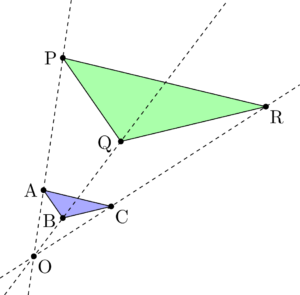
点Oから $\sankaku{ABC}$ の3つの頂点までの距離を3倍にした点をそれぞれP, Q, Rとする。3点P, Q, Rを結んでできる $\sankaku{PQR}$ は $\sankaku{ABC}$ と相似な三角形になる。
このとき,OP, OQ, ORの長さはそれぞれOA, OB, OCの長さの3倍であり,3辺PQ, QR, RPの長さもそれぞれAB, BC, CAの長さの3倍になっている。このように,2つの図形の対応する点を通るすべての直線が点Oを通り,点Oから対応する点までの長さの比がすべて等しいとき,2つの三角形は相似の位置にあるといい,点Oを相似の中心という。
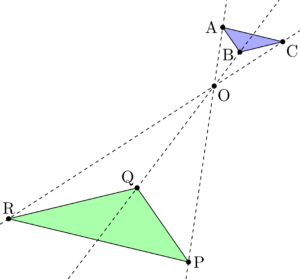
このとき,OP, OQ, ORの長さはそれぞれOA, OB, OCの長さの3倍であり,3辺PQ, QR, RPの長さもそれぞれAB, BC, CAの長さの3倍になっている。このように,2つの図形の対応する点を通るすべての直線が点Oを通り,点Oから対応する点までの長さの比がすべて等しいとき,2つの三角形は相似の位置にあるといい,点Oを相似の中心という。