Contents
部分分数分解を楽に速くする方法

ヒロ
それでは部分分数分解を楽に速くする方法を説明していくことにしよう。
\begin{align*}
\frac{-3x+1}{x(x+3)}=\frac{a}{x}+\frac{b}{x+3}
\end{align*}
$a$ を求める場合は,元の式で分母の $x$ を手で隠して残りの部分に,隠した式が0になる $x$ の値,つまり $x=0$ を代入しよう。
\frac{-3x+1}{x(x+3)}=\frac{a}{x}+\frac{b}{x+3}
\end{align*}
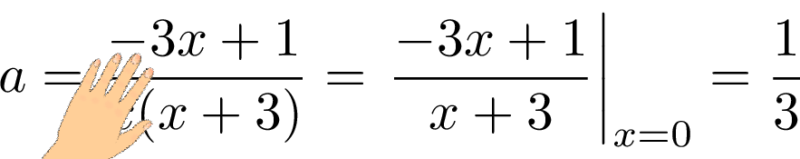
$b$ を求める場合は,元の式で分母の $x+3$ を手で隠して残りの部分に,隠した式が0になる $x$ の値,つまり $x=-3$ を代入しよう。
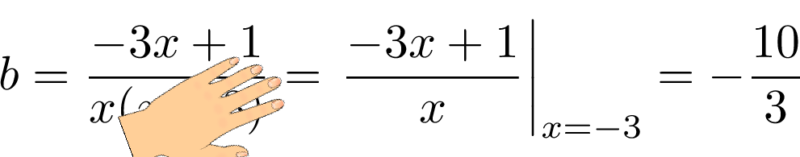

めちゃくちゃ簡単ですね!

ヒロ
積分の問題では,部分分数分解をする過程を書く必要はないから,これでスピードアップ間違いなしだね。
部分分数分解を速くできる理由を知ろう!

ヒロ
次に,何故こんな方法で $a,b$ の値を求めることができて,部分分数分解することができるのかを理解しよう。
\begin{align*}
\frac{-3x+1}{x(x+3)}=\frac{a}{x}+\frac{b}{x+3}
\end{align*}
の両辺に $x$ を掛けると\frac{-3x+1}{x(x+3)}=\frac{a}{x}+\frac{b}{x+3}
\end{align*}
\begin{align*}
\frac{-3x+1}{x+3}=a+\frac{x}{x+3}b
\end{align*}
ここで,$x=0$ を代入すると,$b$ の項が0になるから,$\displaystyle a=\frac{1}{3}$ となる。\frac{-3x+1}{x+3}=a+\frac{x}{x+3}b
\end{align*}
これは結局は,元の分数式の $x$ を手で隠して,隠した式が0になる $x$ を代入することと同じってこと。$b$ を求めたい場合は,元の式の両辺に $x+3$ 掛けて
\begin{align*}
\frac{-3x+1}{x}=\frac{x+3}{x}a+b
\end{align*}
ここで,$x=-3$ を代入すると,$a$ の項が0になるから,$\displaystyle b=-\frac{10}{3}$ となる。\frac{-3x+1}{x}=\frac{x+3}{x}a+b
\end{align*}

なるほど!分かりました。

ヒロ
これで (2) は速く解けるね!


















