Contents
円の方程式

ヒロ
円の定義を考えて,円周上の点がみたすべき等式を導こう。
【円の方程式の導出】
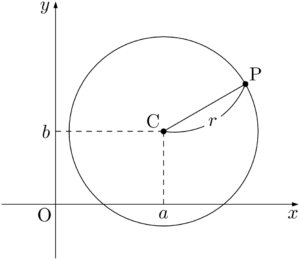
円の中心をC$(a,~b)$,半径を $r$ とする。円周上の点をP$(x,~y)$ とすると,CPの長さが $r$ であるから
\begin{align*}
&\text{CP}^2=r^2 \\[4pt]
&(x-a)^2+(y-b)^2=r^2
\end{align*}
この形を基本形という。&\text{CP}^2=r^2 \\[4pt]
&(x-a)^2+(y-b)^2=r^2
\end{align*}

ヒロ
公式として書いておこう。
円の方程式点$(a,~b)$ を中心とする半径 $r$ の円の方程式は
\begin{align*}
(x-a)^2+(y-b)^2=r^2
\end{align*}
と表される。特に,原点を中心とする半径 $r$ の円の方程式は(x-a)^2+(y-b)^2=r^2
\end{align*}
\begin{align*}
x^2+y^2=r^2
\end{align*}
となる。x^2+y^2=r^2
\end{align*}

ヒロ
ちなみに,半径が1の円のことを単位円ということも覚えておこう。
円の方程式を求める問題【愛媛大】
2018年 愛媛大2点A$(-2,~-1)$ とB$(0,~1)$ について,線分ABを $3:1$ に外分する点を中心とし,点Bを通る円の方程式を求めよ。
【考え方と解答】
円の中心をC$(a,~b)$ とする。線分ABを $3:1$ に外分する点の座標を求めよう。
円の中心をC$(a,~b)$ とする。線分ABを $3:1$ に外分する点の座標を求めよう。
\begin{align*}
&a=\dfrac{3\Cdot0-1\Cdot(-2)}{3-1}=1 \\[4pt]
&b=\dfrac{3\Cdot1-1\Cdot(-1)}{3-1}=2
\end{align*}
よって,円の中心はC$(1,~2)$ である。半径はBCの長さに等しいから&a=\dfrac{3\Cdot0-1\Cdot(-2)}{3-1}=1 \\[4pt]
&b=\dfrac{3\Cdot1-1\Cdot(-1)}{3-1}=2
\end{align*}
\begin{align*}
\text{BC}^2=(1-0)^2+(2-1)^2=2
\end{align*}
したがって,求める円の方程式は\text{BC}^2=(1-0)^2+(2-1)^2=2
\end{align*}
\begin{align*}
(x-1)^2+(y-2)^2=2
\end{align*}
(x-1)^2+(y-2)^2=2
\end{align*}
円の方程式を求める問題【津田塾大】
2011年 津田塾大中心の $x$ 座標が $a$ で,2点$(4,~0)$,$(0,~2)$ を通る円の方程式を求めよ。
【考え方と解答】
まず,円の中心の $y$ 座標を $a$ で表そう。弦の垂直二等分線が円の中心を通ることを利用しよう。A$(4,~0)$,B$(0,~2)$ として,ABの中点をMとすると,M$(2,~1)$ となる。ABの傾きは
まず,円の中心の $y$ 座標を $a$ で表そう。弦の垂直二等分線が円の中心を通ることを利用しよう。A$(4,~0)$,B$(0,~2)$ として,ABの中点をMとすると,M$(2,~1)$ となる。ABの傾きは
\begin{align*}
\dfrac{0-2}{4-0}=-\dfrac{1}{2}
\end{align*}
であるから,ABの垂直二等分線の方程式は\dfrac{0-2}{4-0}=-\dfrac{1}{2}
\end{align*}
\begin{align*}
&y=2(x-2)+1 \\[4pt]
&y=2x-3
\end{align*}
$x=a$ のとき,$y=2a-3$ となるから,円の中心はC$(a,~2a-3)$ となる。半径を $r$ とすると,&y=2(x-2)+1 \\[4pt]
&y=2x-3
\end{align*}
\begin{align*}
r^2&=\text{CA}^2 \\[4pt]
&=(a-4)^2+(2a-3)^2 \\[4pt]
&5a^2-20a+25
\end{align*}
したがって,求める円の方程式はr^2&=\text{CA}^2 \\[4pt]
&=(a-4)^2+(2a-3)^2 \\[4pt]
&5a^2-20a+25
\end{align*}
\begin{align*}
(x-a)^2+(y-(2a-3))^2=5(a^2-4a+5)
\end{align*}
(x-a)^2+(y-(2a-3))^2=5(a^2-4a+5)
\end{align*}


















