問題文に「実数」という単語があり,2文字の対称式が条件として与えられた2変数関数の最大最小問題の考え方と解法を説明します。
問題文に「$x,y$ は実数とする」なんてあっても気にしない人が多いのではないでしょうか。また,与えられている条件式が対称式かどうかを気にしないのも損をしています。
ここでは次のような問題を楽に解けるようになることを目標とします。
Contents
すべての対称式は基本対称式だけで表すことができる

この問題の特徴は与えられている数式が対称式であることだね。

ここで,対称式について,次のことを知っておかなければならない。

つまり今回の問題に出てくる数式は対称式だから,基本対称式の $x+y,~xy$ のみで表せるということだね。

$x+y=u,~xy=v$ とおくと,$2x^2+3xy+2y^2=1$ はどんな式になるかな?

対称式の変形ですね。
&2x^2+3xy+2y^2=1 \\[4pt]&2(x+y)^2-xy=1 \\[4pt]&2u^2-v=1 \\[4pt]&v=2u^2-1~\cdots\cdots ①
\end{align*}

よし,大丈夫だね。

次に $x+y+xy$ を $u,v$ で表すと,$x+y+xy=u+v~\cdots\cdots$ ② となるね。

もうできますね!
x+y+xy&=u+(2u^2-1) \\[4pt]&=2\left(u+\dfrac{1}{4}\right)^2-\dfrac{9}{8}
\end{align*}
$u=-\dfrac{1}{4}$ のとき,最小値 $-\dfrac{9}{8}$ をとる。
最大値は存在しない。

残念ながら間違ってるよ?

え・・・?でもちゃんと条件考えましたよ?

確かに与えられた条件を考えたような気になってるね。

他に条件なんてないと思うんですけど・・・
変数を変換したときは,存在範囲に注意しよう【実数条件】

「$x,y$ は実数」っていうのがあるけどこれは考えないの?

虚数を扱ってるわけじゃないから,別に考えなくても良いんじゃないんですか?

仮に $x,y$ がすべての実数をとったとしても,変数変換したあとの $u,v$ もすべての実数をとるとは言えないんだよ。

そうなんですか?

例えば $(u,v)=(-1,1)$ としてみよう。これに対応する実数の組 $(x,y)$ を求めてみて?

和と積が分かってるから,解と係数の関係で2次方程式作れば求められますね!
&t^2+t+1=0
\end{align*}

確かに,$(u,v)=(-1,1)$ となる実数の組 $(x,y)$ は存在しませんね・・・

いまは1組の $(u,v)$ に対応する $(x,y)$ を考えたけど,これを逆に実数の組 $(x,y)$ からどんな組 $(u,v)$ が存在するのかを考えないといけないね。

次のように考えよう。
&t^2-(x+y)t+xy=0 \\[4pt]&t^2-ut+v=0
\end{align*}
$D\geqq0$ となるから,
&u^2-4v\geqq0
\end{align*}

$x,y$ がすべての実数値を取ったとしても $x+y=u,xy=v$ と置き換えると,$u,v$ には制限がかかるんですね。

実際に $xy$ 平面に図示すると次のようになるよ。


$x+y=u,xy=v$ と置き換えるときは,いつもこの条件を考えないといけないってことですね。

そいういうこと。この条件を忘れたら,入試ではほぼ0点になるだろうね。その結果,解ける人と解けない人の点数差が広がり合否を分ける問題になるってこと。
例題の解答

実数条件の処理は問題で与えられている条件式にかかわらず,同じことを書けば良いため最初に書いてしまおう。

テンプレにするってことですね!

それでは例題の解答を仕上げよう。

任せて下さい!
t^2-ut+v=0
\end{align*}
u^2-4v\geqq0 \cdots\cdots ①
\end{align*}
&2x^2+3xy+2y^2=1 \\[4pt]&2\{(x+y)^2-2xy\}+3xy=1 \\[4pt]&2(u^2-2v)+3v=1 \\[4pt]&v=2u^2-1 \cdots\cdots ②
\end{align*}
&u^2-4(2u^2-1)\geqq0 \\[4pt]&7u^2\leqq4 \\[4pt]&-\dfrac{2}{\sqrt7}\leqq u\leqq\dfrac{2}{\sqrt7}~\cdots\cdots ③
\end{align*}
z&=u+v \\[4pt]&=u+2u^2-1 \\[4pt]&=2\left(u+\dfrac14\right)^2-\dfrac98
\end{align*}
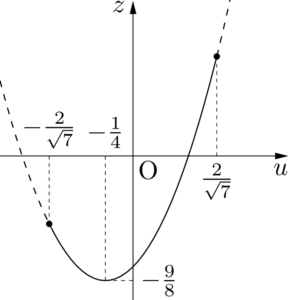
グラフより,$u=-\dfrac14$のとき,$z$は最小値$-\dfrac98$をとり,$u=\dfrac{2}{\sqrt7}$のとき,$z$は最大値
\dfrac{2}{\sqrt7}+2\cdot\dfrac47-1=\dfrac{1+2\sqrt7}{7}
\end{align*}
よって,最大値 $\dfrac{1+2\sqrt7}{7}$,最小値 $-\dfrac89$

最大値も存在するんですね。$u$ の範囲を調べてないと,頂点で最小値をとることも言えないから,ほぼ0点になってしまうんですね。
【2012年 京都大】2文字の対称式の最大最小問題

次の2012年に京都大で出題された入試問題で練習してみよう。
x^2y+xy^2-x^2-2xy-y^2+x+y
\end{align*}

やってみます。
t^2-ut+v=0
\end{align*}
u^2-4v\geqq0 \cdots\cdots ①
\end{align*}
&(x+y)^2-xy=6 \\[4pt]&u^2-v=6 \\[4pt]&v=u^2-6~\cdots\cdots ②
\end{align*}
&u^2-4(u^2-6)\geqq0 \\
&-3u^2+24\geqq0 \\
&u^2\leqq8 \\
&\therefore -2\sqrt2\leqq u\leqq2\sqrt2~\cdots\cdots ③
\end{align*}
z=x^2y+xy^2-x^2-2xy-y^2+x+y
\end{align*}
z&=xy(x+y)-(x+y)^2+(x+y) \\
&=uv-u^2+u \\
&=u(u^2-6)-u^2+u \\
&=u^3-u^2-5u
\end{align*}
\dfrac{dz}{du}&=3u^2-2u-5 \\[4pt]&=(u+1)(3u-5)
\end{align*}
よって,$z$ の増減は次のようになる。
| $u$ | $-2\sqrt{2}$ | $\cdots$ | $-1$ | $\cdots$ | $\dfrac{5}{3}$ | $\cdots$ | $2\sqrt{2}$ |
| $\dfrac{du}{dz}$ | $+$ | $0$ | $-$ | $0$ | $+$ | ||
| $z$ | $-6\sqrt{2}-8$ | $\nearrow$ | $3$ | $\searrow$ | $-\dfrac{175}{27}$ | $\nearrow$ | $6\sqrt{2}-8$ |
増減表より,求める$z$のとりうる値の範囲は
-6\sqrt2-8\leqq z\leqq3
\end{align*}
まとめ

問題文中の対称式と実数という単語には敏感になろう。絶対に実数条件を忘れないようにしよう!




















