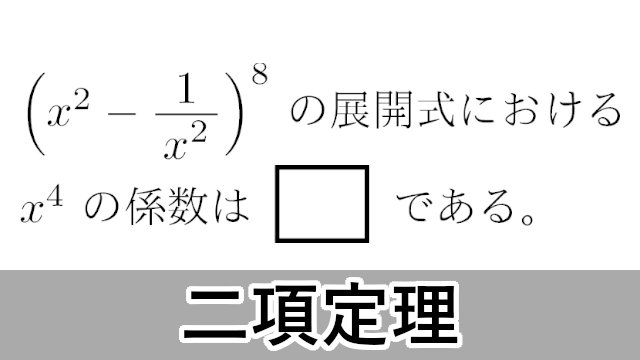
ここでは二項定理について説明します。
2項式の2乗や3乗については,展開公式があるため,公式を利用することで展開することができます。
同じようにして,4乗や5乗についても,公式を作れば良いのでしょうが,それぞれの公式を覚えて使いこなすのは難しいでしょう。
1つずつ公式を作るなら,まとめてn乗で考えて,展開式がどのようになるかという意味を考えた方が楽です。
2項式や3項式のn乗を展開するときに,どのような項が現れて,係数がどうなるのかを知ることで,様々な式を楽に展開することができるようになるでしょう。
Contents
二項定理とは

ヒロ
それでは,まずは二項定理とはどのようなものかを知ろう。
二項定理$(a+b)^n$ を展開すると
\begin{align*}
(a+b)^n=\nCk{n}{0}a^n&+\nCk{n}{1}a^{n-1}b+\cdots \\[4pt]
&\cdots+\nCk{n}{n-1}ab^{n-1}+\nCk{n}{n}a^0b^n
\end{align*}
(a+b)^n=\nCk{n}{0}a^n&+\nCk{n}{1}a^{n-1}b+\cdots \\[4pt]
&\cdots+\nCk{n}{n-1}ab^{n-1}+\nCk{n}{n}a^0b^n
\end{align*}

ヒロ
この等式を意味を説明することなく「頑張って覚えよう!」と言っている授業をみたことがある。

ヒロ
しかし,個人的には二項定理を意味を理解せずに覚えるのは無理,というか「二項定理はそもそも覚えるものではない」と思っている。