【数学ⅡB】二項定理【広島工業大・中部大・立教大】

Contents

二項定理に関する入試問題

2020年広島工業大$(2x+1)^n$ の展開式における $x^2$ の項の係数を264とする。このとき，自然数 $n$ の値を求めよ。

【考え方と解答】
$(2x+1)^n$ の展開式の $x^2$ の項は $\nCk{n}{2}(2x)^2$ であり，$x^2$ の係数が264のとき

\begin{align*}
&\nCk{n}{2}2^2=264 \\[4pt]
&n(n-1)=132 \\[4pt]
&n^2-n-132=0 \\[4pt]
&(n-12)(n+11)=0 \\[4pt]
&n=12,~-11
\end{align*}

$n$ は自然数であるから，$n=12$

二項定理に関する入試問題2

2018年中部大・改次の式の値を求めよ。

\begin{align*}
\nCk{8}{0}-\nCk{8}{1}2^{-1}+\nCk{8}{2}2^{-2}-\nCk{8}{3}2^{-3}+\cdots-\nCk{8}{7}2^{-7}+\nCk{8}{8}2^{-8}
\end{align*}

【考え方と解答】
式の形から「与えられた式は二項定理を用いて展開した式」だと思えるようにしよう。

\begin{align*}
(与式)&=\nCk{8}{0}-\nCk{8}{1}2^{-1}+\nCk{8}{2}2^{-2}-\nCk{8}{3}2^{-3}+\cdots-\nCk{8}{7}2^{-7}+\nCk{8}{8}2^{-8} \\[4pt]&=\nCk{8}{0}\Cdota(-1)^8+\nCk{8}{1}\Cdota\dfrac{1}{2}\Cdota(-1)^7+\nCk{8}{2}\left(\dfrac{1}{2}\right)^2\Cdota(-1)^6-\nCk{8}{3}\left(\dfrac{1}{2}\right)^2\Cdota(-1)^6+ \\[4pt]&　　　\cdots-\nCk{8}{7}\left(\dfrac{1}{2}\right)^7\Cdota(-1)+\nCk{8}{8}\left(\dfrac{1}{2}\right)^8 \\[4pt]&=\left(-1+\dfrac{1}{2}\right)^8=\left(-\dfrac{1}{2}\right)^8 \\[4pt]&=\dfrac{1}{256}
\end{align*}

二項定理に関する入試問題

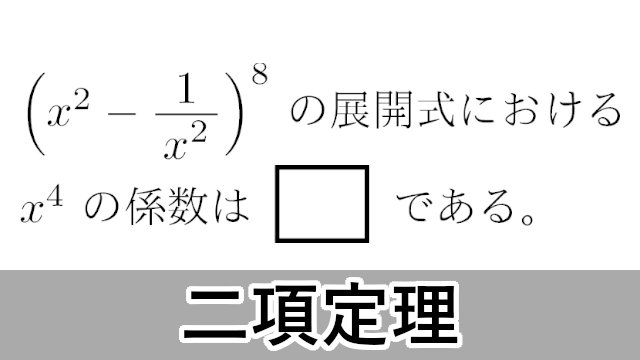
2019年立教大$\left(x^2-\dfrac{1}{x^2}\right)^8$ の展開式における $x^4$ の係数は $\myhako$ である。

【考え方と解答】
$\left(x^2-\dfrac{1}{x^2}\right)^8$ の展開式の一般項は

\begin{align*}
\nCk{8}{k}(x^2)^k\left(-\dfrac{1}{x^2}\right)^{8-k}=(-1)^{8-k}\nCk{8}{k}x^{4k-16}
\end{align*}

となり，これが $x^4$ の項を表すときを考えて

\begin{align*}
&4x-16=4 \\[4pt]
&k=5
\end{align*}

よって，求める $x^4$ の係数は

\begin{align*}
(-1)^{8-5}\nCk{8}{5}&=-\nCk{8}{3}=-56
\end{align*}