2つの曲線の間の面積を求める方法を説明します。
これまでで面積を求めることができる図形は「三角形,台形,平行四辺形,円」などです。定積分による面積の求め方を知ることで,曲線で囲まれる部分の図形の面積も求めることができるようになります。
定積分による面積の求め方をしっかり理解しましょう。
曲線と $x$ 軸の間の部分の面積

ヒロ
曲線と $x$ 軸の間の部分の面積を求める公式は次のようになっている。
定積分で面積を求める区間 $a\leqq x\leqq b$ において,常に $f(x)\geqq0$ であるとき,曲線 $y=f(x)$ と $x$ 軸,および2直線 $x=a,~x=b$ で囲まれた部分の面積 $S$ は次のようになる。
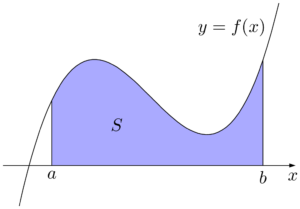
区間 $a\leqq x\leqq b$ において,常に $f(x)\leqq0$ であるとき,曲線 $y=f(x)$ と $x$ 軸,および2直線 $x=a,~x=b$ で囲まれた部分の面積 $S$ は次のようになる。
\begin{align*}
S=\dint{a}{b}f(x)\;dx
\end{align*}
S=\dint{a}{b}f(x)\;dx
\end{align*}

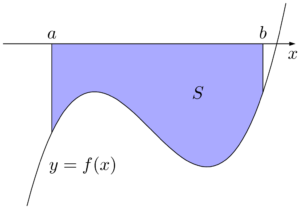
区間 $a\leqq x\leqq b$ において,常に $f(x)\leqq0$ であるとき,曲線 $y=f(x)$ と $x$ 軸,および2直線 $x=a,~x=b$ で囲まれた部分の面積 $S$ は次のようになる。
\begin{align*}
S=\dint{a}{b}\{-f(x)\}\;dx
\end{align*}
S=\dint{a}{b}\{-f(x)\}\;dx
\end{align*}


ヒロ
グラフが $x$ 軸の上側にあればそのまま積分し,$x$ 軸の下側にあれば $-1$ をかけて積分することで面積を求めることができる。
2つの曲線の間の面積

ヒロ
次に,2つの曲線の間の面積を求める公式は次のようになっている。
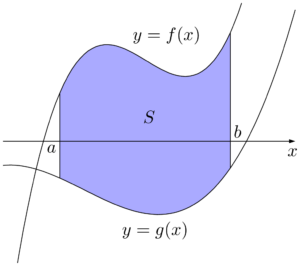
2つの曲線の間の面積区間 $a\leqq x\leqq b$ において,常に $f(x)\geqq g(x)$ であるとき,2曲線 $y=f(x)$,$y=g(x)$ および2直線 $x=a,~x=b$ で囲まれた部分の面積 $S$ は次のようになる。
\begin{align*}
S=\dint{a}{b}\{f(x)-g(x)\}\;dx
\end{align*}
S=\dint{a}{b}\{f(x)-g(x)\}\;dx
\end{align*}


ヒロ
実はこの公式だけ覚えていれば,最初の公式を覚える必要はない。それは $x$ 軸の方程式は $y=0$ だからである。
2020年 学習院大
2020年 学習院大$a$ を実数とし,2つの放物線
(1) $S$ を求めよ。
(2) $a$ が実数全体を動くとき,$S$ の最小値と最小値を与える $a$ の値を求めよ。
\begin{align*}
C_1:y=x^2+1,~C_2:y=1-2(x-1)^2
\end{align*}
と2つの直線 $x=a,~x=a+1$ とで囲まれる図形の面積の面積を $S$ とする。C_1:y=x^2+1,~C_2:y=1-2(x-1)^2
\end{align*}
(1) $S$ を求めよ。
(2) $a$ が実数全体を動くとき,$S$ の最小値と最小値を与える $a$ の値を求めよ。
【解答と考え方】
まずは,2つの放物線が $a\leqq x\leqq a+1$ の間に共有点をもっているかどうかを調べよう。もし共有点が存在するなら,その点の前後で上下関係が変わっている可能性がある(接している場合は上限関係は変わらない)ので,積分区間を分けて定積分の計算を行う必要がある。
$C_1,~C_2$ の方程式を連立して $y$ を消去すると

よって,求める面積 $S$ は次のようになる。
まずは,2つの放物線が $a\leqq x\leqq a+1$ の間に共有点をもっているかどうかを調べよう。もし共有点が存在するなら,その点の前後で上下関係が変わっている可能性がある(接している場合は上限関係は変わらない)ので,積分区間を分けて定積分の計算を行う必要がある。
$C_1,~C_2$ の方程式を連立して $y$ を消去すると
\begin{align*}
&x^2+1=1-2(x-1)^2 \\[4pt]
&3x^2-4x+2=0~\cdots\cdots①
\end{align*}
この方程式の判別式を $D$ とすると&x^2+1=1-2(x-1)^2 \\[4pt]
&3x^2-4x+2=0~\cdots\cdots①
\end{align*}
\begin{align*}
\dfrac{D}{4}&=4-6=-2<0 \end{align*}
となるから,①は実数解をもたない。つまり,$C_1,~C_2$ は共有点をもたず,区間 $a\leqq x\leqq a+1$ において,常に $C_1$ が $C_2$ の上側にある。実際に2つの曲線のグラフを描いても分かる。\dfrac{D}{4}&=4-6=-2<0 \end{align*}

よって,求める面積 $S$ は次のようになる。
\begin{align*} S&=\dint{a}{a+1}\{(x^2+1)-1+2(x-1)^2\}\;dx \\[4pt] &=\dint{a}{a+1}(3x^2-4x+2)\;dx \\[4pt] &=\tint{x^3-2x^2+2x}{a}{a+1} \\[4pt] &=(a+1)^3-a^3-2\{(a+1)^2-a^2\}+2\{(a+1)-a\} \\[4pt] &=3a^2+3a+1-2(2a+1)+2 \\[4pt] &=3a^2-a+1 \end{align*}
(2) $a$ が実数全体を動くとき,$S$ の最小値と最小値を与える $a$ の値を求めよ。
【解答と考え方】
\begin{align*} S&=3a^2-a+1 \\[4pt] &=3\left(a-\dfrac{1}{6}\right)^2+\dfrac{11}{12} \end{align*}
よって,$S$ は $a=\dfrac{1}{6}$ のとき最小値 $\dfrac{11}{12}$ をとる。

















