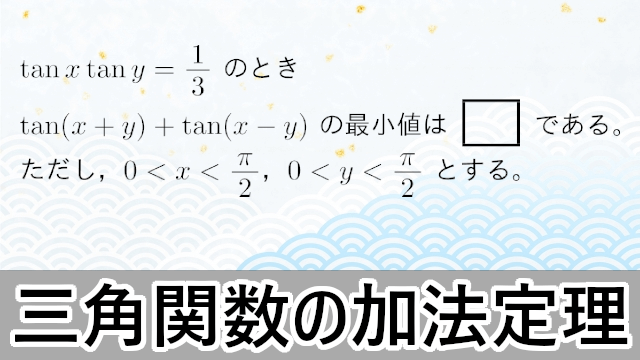
ここでは,三角関数の加法定理について説明します。
三角関数の加法定理を正確に覚えて,使いこなせるようにすることが重要です。
しかし,東京大学でも加法定理の導出が出題されているため,その証明も出来るようにしておいた方が良いでしょう。
次の記事ではベクトルを用いた証明を載せています。
Contents
三角関数の加法定理

ヒロ
まず,三角関数の加法定理とは,次のようなものである。
三角関数の加法定理

ヒロ
数学が苦手な人は,導出を後回しにして,加法定理を使って問題を解けるようにするのが良いだろう。
【加法定理の覚え方の例】
角については $\alpha,~\beta$ の順になっているため,サインとコサインについてはその順番だけを覚えれば良い。
正弦(サイン)の加法定理の覚え方として有名なものは「咲いたコスモスコスモス咲いた」だろう。「咲いた」が $\sin$ を表し,「コスモス」が $\cos$ を表している。つまり,「サインコサインコサインサイン」の順になっていることを表している。角が $\alpha+\beta$ のように和になっていれば,右辺もそのまま和にすれば良い。
余弦(コサイン)の加法定理の覚え方として有名なものに「コスモスコスモス咲かない咲かない」がある。「コスモス」が $\cos$ を表し「咲かない」が $\sin$ を表している。「咲かない」と否定形になっていることで「マイナスイメージ」があり,$\cos\alpha\cos\beta$ と $\sin\alpha\sin\beta$ の間が「マイナス」であることにつながっている。
正接(タンジェント)の加法定理の覚え方として有名なものは「1マイタンタンタンプラタン」がある。分母,分子の順に省略しながら読んでいるだけである。「マイ」はマイナス,「プラ」はプラス,「タン」は $\tan$ を表している。