ここでは2次不等式を含む連立不等式の解き方を説明します。
「連立」と付いても連立方程式のように未知数が複数あるわけではなく，未知数は1つです。
複数の不等式を満たす未知数の値の範囲を求めるだけです。
連立不等式を解くこと自体は少しの練習で出来るようになるはずですが，多くの場合，問題となるのは連立不等式を立てることができるかどうかです。
与えられた条件から正しく不等式を立てて解くことができるようになりましょう。
連立不等式に関する問題
ヒロ
実際に定期テストで出題された問題を解いてみよう。
問題連立不等式 $\begin{cases}
x^2-2x>1 \\[4pt]
x^2-x<6 \end{cases}$ を解け。
x^2-2x>1 \\[4pt]
x^2-x<6 \end{cases}$ を解け。
ヒロ
それぞれの不等式を解いて，共通範囲を考えよう。
【考え方と解答】
$x^2-2x>1$ より $x^2-2x-1>0$ 左辺は有理数の範囲で因数分解できないから，解の公式を利用して $x^2-2x-1=0$ を満たす $x$ を求める。 $x^2-2x-1=0$ を解くと，$x=1\pm\sqrt{2}$ であるから，$x^2-2x-1>0$ の解は
\begin{align*} x<1-\sqrt{2},~1+\sqrt{2}<x\cdots\cdots① \end{align*}
$x^2-x<6$ より \begin{align*} &x^2-x-6<0 \\[4pt] &(x-3)(x+2)<0 \\[4pt] &-2<x<3\cdots\cdots② \end{align*}
①，②の共通部分を求めて \begin{align*} -2<x<1-\sqrt{2},~1+\sqrt{2}<x<3 \end{align*}
連立不等式に関する問題2
ヒロ
次も定期テストで出題された問題。
問題2次方程式 $x^2-2ax+3a=0\cdots\cdots①$, $x^2+ax+1=0\cdots\cdots②$ について次の問いに答えよ。
(1) ①，②がともに実数解をもつような $a$ の値の範囲を求めよ。
(2) 少なくとも一方が実数解をもつような $a$ の値の範囲を求めよ。
(1) ①，②がともに実数解をもつような $a$ の値の範囲を求めよ。
(2) 少なくとも一方が実数解をもつような $a$ の値の範囲を求めよ。
ヒロ
「実数解をもつ」と書かれている場合は，「少なくとも1個もつ」と考えよう。
【(1)の考え方と解答】
①，②の判別式をそれぞれ $D_1,~D_2$ とすると
①，②の判別式をそれぞれ $D_1,~D_2$ とすると
\begin{align*}
\dfrac{D_1}{4}=a^2-3a,~D_2=a^2-4
\end{align*}
①，②がともに実数解をもつとき\dfrac{D_1}{4}=a^2-3a,~D_2=a^2-4
\end{align*}
\begin{align*}
D_1\geqq0~かつ~D_2\geqq0
\end{align*}
であるからD_1\geqq0~かつ~D_2\geqq0
\end{align*}
\begin{align*}
&\begin{cases}
a^2-3a\geqq0 \\[4pt]
a^2-4\geqq0
\end{cases} \\[4pt]
&\begin{cases}
a(a-3)\geqq0 \\[4pt]
(a-2)(a+2)\geqq0
\end{cases} \\[4pt]
&\begin{cases}
a\leqq0,~3\leqq a \\[4pt]
a\leqq-2,~2\leqq a
\end{cases}
\end{align*}
したがって，求める $a$ の値の範囲は $a\leqq-2,~3\leqq a$&\begin{cases}
a^2-3a\geqq0 \\[4pt]
a^2-4\geqq0
\end{cases} \\[4pt]
&\begin{cases}
a(a-3)\geqq0 \\[4pt]
(a-2)(a+2)\geqq0
\end{cases} \\[4pt]
&\begin{cases}
a\leqq0,~3\leqq a \\[4pt]
a\leqq-2,~2\leqq a
\end{cases}
\end{align*}
(2) 少なくとも一方が実数解をもつような $a$ の値の範囲を求めよ。
【(2)の考え方と解答】
①，②のうち，少なくとも一方が実数解をもつとき
①，②のうち，少なくとも一方が実数解をもつとき
\begin{align*}
D_1\geqq0~または~D_2\geqq0
\end{align*}
したがって，求める $a$ の値の範囲は $a\leqq0,~2\leqq a$D_1\geqq0~または~D_2\geqq0
\end{align*}
連立不等式を満たす整数の個数に関する問題
ヒロ
不等式を満たす整数の個数に関する問題にも強くなっておこう。
問題連立不等式 $\begin{cases}
3x^2+11x>4 \\[4pt]
x^2-(a+1)x+a\leqq0
\end{cases}$ を満たす整数 $x$ がちょうど3個存在するとき，定数 $a$ の値の範囲を求めよ。
3x^2+11x>4 \\[4pt]
x^2-(a+1)x+a\leqq0
\end{cases}$ を満たす整数 $x$ がちょうど3個存在するとき，定数 $a$ の値の範囲を求めよ。
ヒロ
まずはそれぞれの不等式を解こう。
【考え方と解答】
$3x^2+11x>4$ より
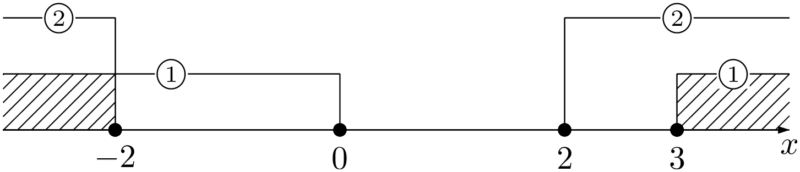
(i) $a<1$ のとき ①と②の共通部分は次の斜線部分である。
$\dfrac{1}{3}<x\leqq1$ に整数が1つ（$x=1$）含まれるから，$a\leqq x<4$ に整数がちょうど2個存在するような $a$ の値の範囲を考える。 含まれる2個の整数は $x=-6,~-5$ であるから，$x=a$ が含まれることに注意すると，
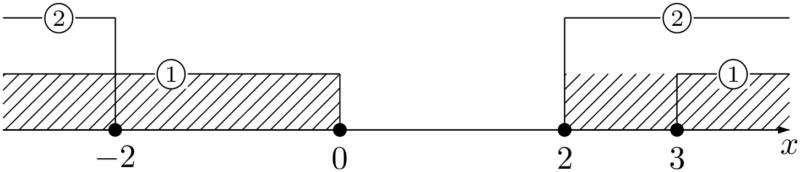
(iii) $a>1$ のとき ①と④の共通部分は次の斜線部分である。
$1\leqq x\leqq a$ に整数がちょうど3個存在するとき，その整数は $x=1,~2,~3$ である。$x=a$ が含まれることに注意すると，$a$ の値の範囲は $3\leqq a<4$ である。 以上より，求める $a$ の値の範囲は，
$3x^2+11x>4$ より
\begin{align*} &(x+4)(3x-1)>0 \\[4pt] &x<-4,~\dfrac{1}{3}<x~\cdots\cdots① \end{align*}
$x^2-(a+1)x+a\leqq0$ より \begin{align*} (x-1)(x-a)\leqq0 \end{align*}
$a$ の値によって不等式の解が変わるので場合分けをしよう。 \begin{align*} \begin{cases} a<1~のとき~~a\leqq x\leqq 1 ~ &\cdots\cdots② \\[4pt] a=1~のとき~~x=1 ~ &\cdots\cdots③ \\[4pt] a>1~のとき~~1\leqq x\leqq a ~ &\cdots\cdots④ \end{cases} \end{align*}
3つのそれぞれについて連立不等式を満たす整数 $x$ がちょうど3個存在するときの $a$ の値の範囲を考えよう。(i) $a<1$ のとき ①と②の共通部分は次の斜線部分である。
$\dfrac{1}{3}<x\leqq1$ に整数が1つ（$x=1$）含まれるから，$a\leqq x<4$ に整数がちょうど2個存在するような $a$ の値の範囲を考える。 含まれる2個の整数は $x=-6,~-5$ であるから，$x=a$ が含まれることに注意すると，
\begin{align*} -7<a\leqq-6 \end{align*}
(ii) $a=1$ のとき ①と③を同時に満たす整数は $x=1$ のみの1個だから条件を満たさない。(iii) $a>1$ のとき ①と④の共通部分は次の斜線部分である。
$1\leqq x\leqq a$ に整数がちょうど3個存在するとき，その整数は $x=1,~2,~3$ である。$x=a$ が含まれることに注意すると，$a$ の値の範囲は $3\leqq a<4$ である。 以上より，求める $a$ の値の範囲は， \begin{align*} -7<a\leqq-6,~3\leqq a<4 \end{align*}