定積分を含む不等式の証明の第三弾です。具体的な入試問題を扱って説明します。
Contents
2006年 東北学院大の入試問題の考え方
\dfrac{1}{2}+\dfrac{1}{3}+\cdots\dfrac{1}{n}<\log n
\end{align*}

この問題では「定積分を用いて」とあるから,$\dfrac{1}{x}$ の原始関数を考えると $\log\abs{x}$ となることが頭に浮かぶ。
\log n=\dint{1}{n}\dfrac{1}{x}\;dx
\end{align*}


ということで,右辺を面積として捉えたのだから,左辺も面積として捉えよう。

また,今回は不等式の証明をするのだから,上図の斜線部分の面積より小さくなるような図形として,左辺を捉えなければならない。

そのために,もう一度グラフを見て,左辺の式を図形として捉えていこう。
\dfrac{1}{2},~\dfrac{1}{3},~\dfrac{1}{4},~\cdots,~\dfrac{1}{n}
\end{align*}
f(2),~f(3),~f(4),~\cdots,~f(n)
\end{align*}
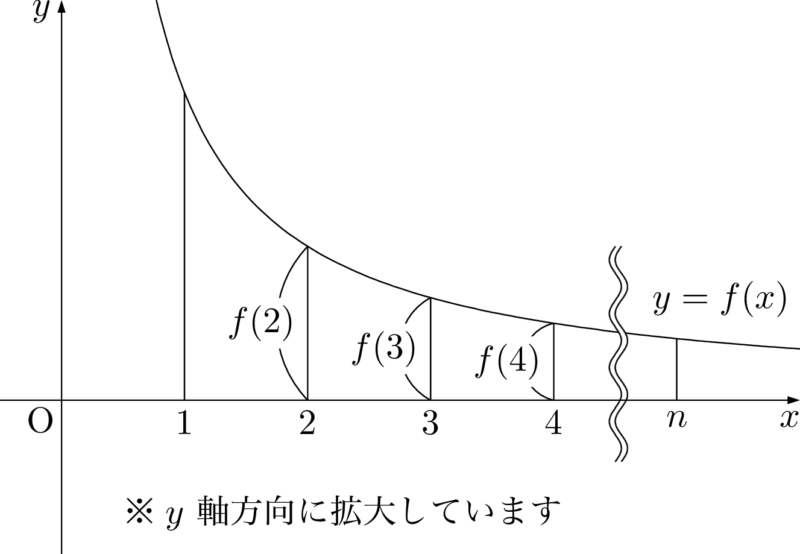
ここで,
f(2)+f(3)+f(4)+\cdots+f(n)
\end{align*}

ただ,ここで1つの疑問が生じる。左側と右側のどちらに長方形を作るのか?
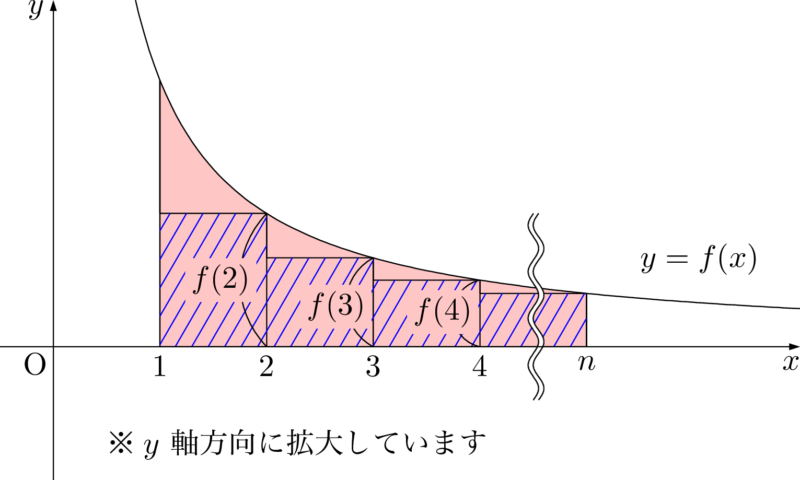
【右側に長方形を作った場合】
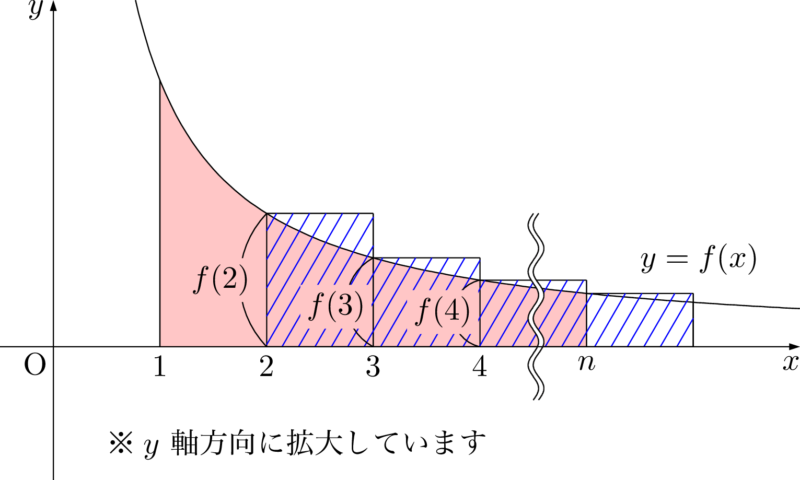

いま,証明したいことは,赤色部分の面積が青色斜線部分より大きいことだね。どちらの図で考えると,簡単に証明できるかを考えよう。両端が揃っている図で考えた方が,楽だろうということは分かるはず。
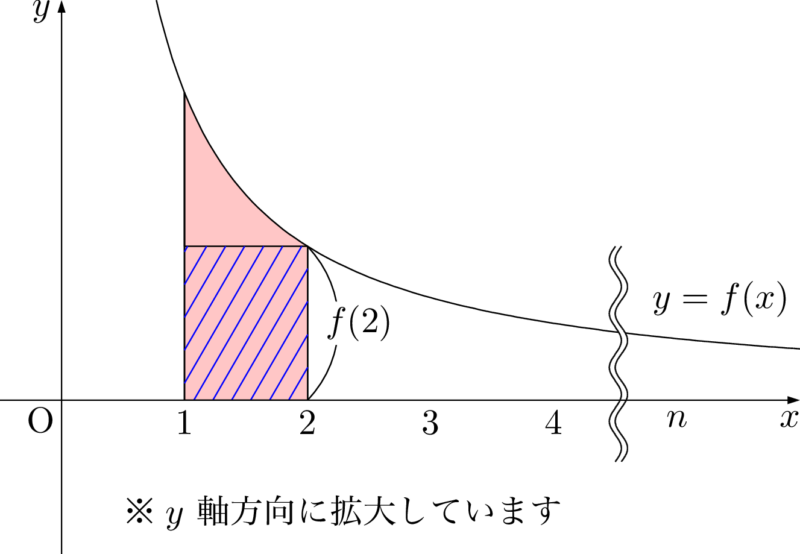

このことが $1\leqq x\leqq 2$, $2\leqq x\leqq3$, $\cdots, n-1\leqq x\leqq n$ のすべての部分で成り立つことを証明すれば良い。

一気に証明するために文字を利用しよう。つまり,$k\leqq x\leqq k+1~(k=1,~2,~\cdots,~n-1)$ において,斜線部分の面積が赤色部分の面積より小さいことを証明しよう。
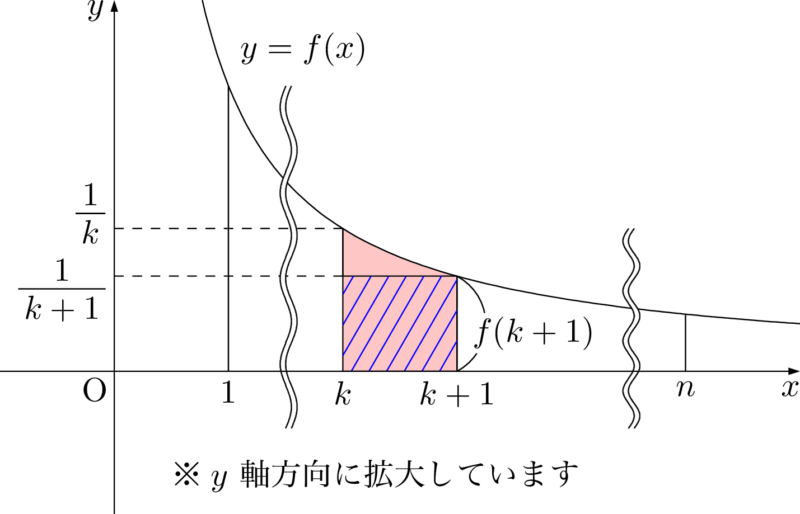
常には等号は成り立たないから,
&\dint{k}{k+1}\dfrac{1}{k+1}\;dx<\dint{k}{k+1}\dfrac{1}{x}\;dx \\[4pt]
&\dfrac{1}{k+1}<\dint{k}{k+1}\dfrac{1}{x}\;dx
\end{align*}

左辺の定積分は,$\dfrac{1}{k+1}$ が $x$ によらない定数であることに注意しよう。積分範囲が1だから,被積分関数である $\dfrac{1}{k+1}$ がそのまま出てくる。というか,そもそも幅1,高さ $\dfrac{1}{k+1}$ の長方形の面積を考えているから,この結果は当然であるともいえる。

上の不等式は $k$ が自然数であれば成り立つことを利用すれば,与えられた不等式の証明はできるね。
&\dfrac{1}{2}<\dint{1}{2}\dfrac{1}{x}\;dx \\[4pt]
&\dfrac{1}{3}<\dint{2}{3}\dfrac{1}{x}\;dx \\[4pt]
&\quad\quad\vdots \\[4pt]
&\dfrac{1}{n}<\dint{n-1}{n}\dfrac{1}{x}\;dx
\end{align*}
&\dfrac{1}{2}+\dfrac{1}{3}+\cdots+\dfrac{1}{n}<\dint{1}{2}\dfrac{1}{x}\;dx+\dint{2}{3}\dfrac{1}{x}\;dx+\cdots+\dint{n-1}{n}\dfrac{1}{x}\;dx
\end{align*}
(右辺)&=\dint{1}{n}\dfrac{1}{x}\;dx=\log n
\end{align*}
\dfrac{1}{2}+\dfrac{1}{3}+\cdots+\dfrac{1}{n}<\log n
\end{align*}


















