ここでは三角比を含む方程式について解説します。
常に三角比の定義「サインはy座標,コサインはx座標,タンジェントは傾き」を意識しましょう。
単位円と三角比の値の位置関係

ヒロ
まずはサインとコサインの値が与えられたときに,描く必要がある直線の書き方をマスターしよう。

ヒロ
三角定規に現れる角度のサインやコサインの値で正のものは $\dfrac{1}{2},~\dfrac{1}{\sqrt{2}},~\dfrac{\sqrt{3}}{2}$ である。

ヒロ
このうち,描くのが最も簡単な $\dfrac{1}{2}$ から説明する。
【直線 $x=\dfrac{1}{2}$ の描き方】
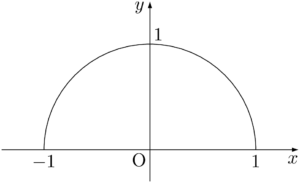
原点を中心とする半径1の半円(上半分)を描こう。
直線 $x=\dfrac{1}{2}$ を描きたいときは,点 $\left(\dfrac{1}{2},~0\right)$ (図の赤い点)を通り $x$ 軸に垂直な直線を描こう。
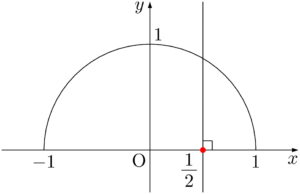
原点を中心とする半径1の半円(上半分)を描こう。

直線 $x=\dfrac{1}{2}$ を描きたいときは,点 $\left(\dfrac{1}{2},~0\right)$ (図の赤い点)を通り $x$ 軸に垂直な直線を描こう。

【直線 $y=\dfrac{1}{2}$ の描き方】
直線 $y=\dfrac{1}{2}$ も同じように簡単に描くことができる。点 $\left(0,~\dfrac{1}{2}\right)$ (図の赤い点)を通り $y$ 軸に垂直な直線を描くだけだ。
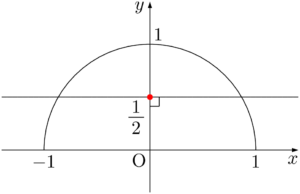
直線 $y=\dfrac{1}{2}$ も同じように簡単に描くことができる。点 $\left(0,~\dfrac{1}{2}\right)$ (図の赤い点)を通り $y$ 軸に垂直な直線を描くだけだ。

【2直線 $x=\dfrac{1}{\sqrt{2}},~y=\dfrac{1}{\sqrt{2}}$ の描き方】
直線 $x=\dfrac{1}{\sqrt{2}}$ の描き方を知ろう。そのために
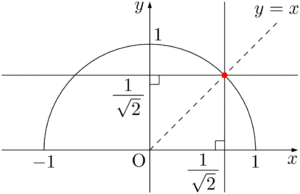
直線 $x=\dfrac{1}{\sqrt{2}}$ の描き方を知ろう。そのために
\begin{align*}
\left(\dfrac{1}{\sqrt{2}}\right)^2+\left(\dfrac{1}{\sqrt{2}}\right)^2=1
\end{align*}
であることを知っておこう。つまり,直線 $y=x$ と半円の交点が $\left(\dfrac{1}{\sqrt{2}},~\dfrac{1}{\sqrt{2}}\right)$ である。したがって,点 $\left(\dfrac{1}{\sqrt{2}},~\dfrac{1}{\sqrt{2}}\right)$ (図の赤い点)を通るように各座標軸に垂直な直線を引くことで,直線 $x=\dfrac{1}{\sqrt{2}}$ や線 $y=\dfrac{1}{\sqrt{2}}$ を簡単に描くことができる。\left(\dfrac{1}{\sqrt{2}}\right)^2+\left(\dfrac{1}{\sqrt{2}}\right)^2=1
\end{align*}

【直線 $x=\dfrac{\sqrt{3}}{2}$ の描き方】
次は直線 $x=\dfrac{\sqrt{3}}{2}$ の描き方を知ろう。$x$ 座標が $\dfrac{\sqrt{3}}{2}$ になる点を正確に取るのは少し難しいため工夫する。青い点 $\left(0,~\dfrac{1}{2}\right)$ を利用して直線 $y=\dfrac{1}{2}$(破線)を引いて半円との交点(図の赤い点)をとる。実際には破線を引かずに,赤い点の位置を一瞬で取れるようにすると良い。
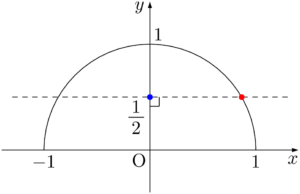
赤い点の $x$ 座標は $\dfrac{\sqrt{3}}{2}$ であるから,赤い点を通り,$x$ 軸に垂直な直線の方程式が $x=\dfrac{\sqrt{3}}{2}$ となる。
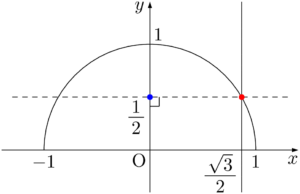
次は直線 $x=\dfrac{\sqrt{3}}{2}$ の描き方を知ろう。$x$ 座標が $\dfrac{\sqrt{3}}{2}$ になる点を正確に取るのは少し難しいため工夫する。青い点 $\left(0,~\dfrac{1}{2}\right)$ を利用して直線 $y=\dfrac{1}{2}$(破線)を引いて半円との交点(図の赤い点)をとる。実際には破線を引かずに,赤い点の位置を一瞬で取れるようにすると良い。

赤い点の $x$ 座標は $\dfrac{\sqrt{3}}{2}$ であるから,赤い点を通り,$x$ 軸に垂直な直線の方程式が $x=\dfrac{\sqrt{3}}{2}$ となる。

【直線 $y=\dfrac{\sqrt{3}}{2}$ の描き方】
最後に直線 $y=\dfrac{\sqrt{3}}{2}$ の描き方を知ろう。青い点 $\left(\dfrac{1}{2},~0\right)$ を利用して直線 $x=\dfrac{1}{2}$(破線)を引いて半円との交点(図の赤い点)をとる。先程と同様に,実際には破線を引かず,赤点の位置を取れるようにすると良い。
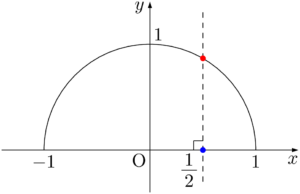
赤い点の $y$ 座標は $\dfrac{\sqrt{3}}{2}$ であるから,赤い点を通り,$y$ 軸に垂直な直線の方程式が $y=\dfrac{\sqrt{3}}{2}$ となる。
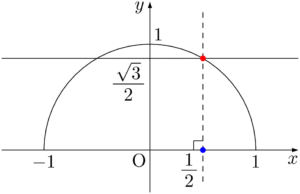
最後に直線 $y=\dfrac{\sqrt{3}}{2}$ の描き方を知ろう。青い点 $\left(\dfrac{1}{2},~0\right)$ を利用して直線 $x=\dfrac{1}{2}$(破線)を引いて半円との交点(図の赤い点)をとる。先程と同様に,実際には破線を引かず,赤点の位置を取れるようにすると良い。

赤い点の $y$ 座標は $\dfrac{\sqrt{3}}{2}$ であるから,赤い点を通り,$y$ 軸に垂直な直線の方程式が $y=\dfrac{\sqrt{3}}{2}$ となる。


ヒロ
上で描いた直線を自由に描くことができれば,赤い点を第2象限にとることで $x=-\dfrac{1}{2}$, $x=-\dfrac{1}{\sqrt{2}}$, $x=-\dfrac{\sqrt{3}}{2}$ も簡単に描くことができるだろう。

ヒロ
次はタンジェントの値が与えられたときに,描く必要がある直線の書き方をマスターしよう。

ヒロ
$y=x$, $y=\sqrt{3}x$, $y=\dfrac{1}{\sqrt{3}}x$ の3種類を描けるようになる必要があるが,直線 $y=x$ は簡単なのでそれ以外の直線を描けるようにしよう。
【直線 $y=\sqrt{3}x$ の描き方】
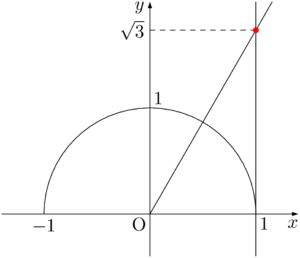
$y=\sqrt{3}x$ のグラフは原点を通り,傾きが $\sqrt{3}$ である直線であるから,次の図のように,赤い点 $(1,~\sqrt{3})$ と原点を結んだ直線が $y=\sqrt{3}x$ である。
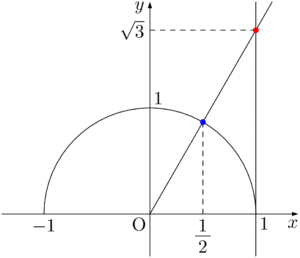
$y$ 座標が $\sqrt{3}$ になるような点を正確に取るのが難しく感じる人は,$x$ 座標が $\dfrac{1}{2}$ である半円上の点(青い点)を通るようにすると良い。
$y=\sqrt{3}x$ のグラフは原点を通り,傾きが $\sqrt{3}$ である直線であるから,次の図のように,赤い点 $(1,~\sqrt{3})$ と原点を結んだ直線が $y=\sqrt{3}x$ である。

$y$ 座標が $\sqrt{3}$ になるような点を正確に取るのが難しく感じる人は,$x$ 座標が $\dfrac{1}{2}$ である半円上の点(青い点)を通るようにすると良い。

【直線 $y=\dfrac{1}{\sqrt{3}}x$ の描き方】
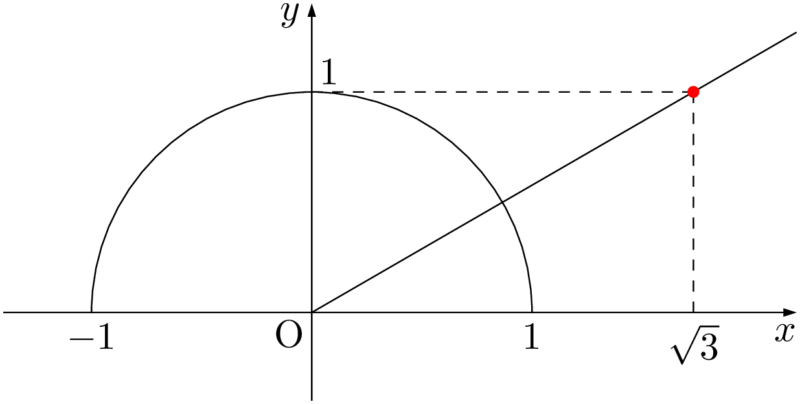
直線 $x=1$ 上の点で $y$ 座標が $\dfrac{1}{\sqrt{3}}$ である点をとることが難しいので工夫する。傾きが $\dfrac{1}{\sqrt{3}}$ であるから,次の図のように,赤い点 $(\sqrt{3},~1)$ と原点を結んだ直線が $y=\dfrac{1}{\sqrt{3}}x$ である。
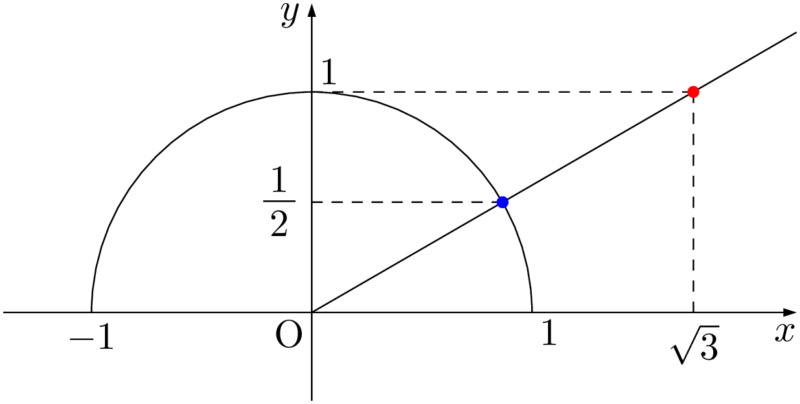
$x$ 座標が $\sqrt{3}$ になるような点を正確に取るのが難しく感じる人は,$y$ 座標が $\dfrac{1}{2}$ である半円上の点(青い点)を通るようにすると良い。
赤い点を第2象限にとると同じようにして $y=-\sqrt{3}x$, $y=-\dfrac{1}{\sqrt{3}}x$ も簡単に描くことができるだろう。
直線 $x=1$ 上の点で $y$ 座標が $\dfrac{1}{\sqrt{3}}$ である点をとることが難しいので工夫する。傾きが $\dfrac{1}{\sqrt{3}}$ であるから,次の図のように,赤い点 $(\sqrt{3},~1)$ と原点を結んだ直線が $y=\dfrac{1}{\sqrt{3}}x$ である。

$x$ 座標が $\sqrt{3}$ になるような点を正確に取るのが難しく感じる人は,$y$ 座標が $\dfrac{1}{2}$ である半円上の点(青い点)を通るようにすると良い。
赤い点を第2象限にとると同じようにして $y=-\sqrt{3}x$, $y=-\dfrac{1}{\sqrt{3}}x$ も簡単に描くことができるだろう。

三角比を含む方程式の問題
問題$0\Deg\leqq\theta\leqq180\Deg$ のとき,次の等式を満たす $\theta$ を求めよ。
(1) $\sin\theta=\dfrac{1}{2}$
(2) $\cos\theta=\dfrac{1}{\sqrt{2}}$
(3) $\tan\theta=-\sqrt{3}$
(1) $\sin\theta=\dfrac{1}{2}$
(2) $\cos\theta=\dfrac{1}{\sqrt{2}}$
(3) $\tan\theta=-\sqrt{3}$
【(1)の考え方と解答】
サインは $y$ 座標を表すから,直線 $y=\dfrac{1}{2}$ を引いて半円との交点(図の赤い点)を得る。
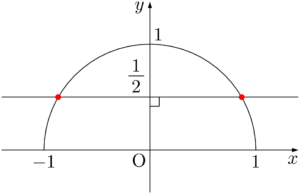
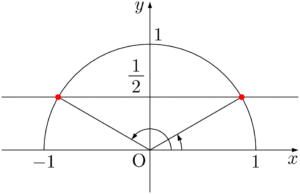
求める角 $\theta$ は,原点と赤い点を結んだ線分と $x$ 軸の正の向きとで作られる角で,2つある。
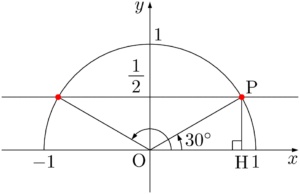
次の図で $\sankaku{OPH}$ は $\text{PH}:\text{OP}:\text{OH}=1:2:\sqrt{3}$ の直角三角形であるから,$\kaku{POH}=30\Deg$ である。
半円上で $y$ 座標が $\dfrac{1}{2}$ であるもう1つの点をQとすると対称性から $\kaku{HOQ}=150\Deg$ と分かる。
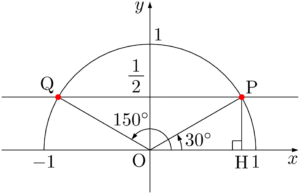
したがって,$\theta=30\Deg,~150\Deg$
サインは $y$ 座標を表すから,直線 $y=\dfrac{1}{2}$ を引いて半円との交点(図の赤い点)を得る。

求める角 $\theta$ は,原点と赤い点を結んだ線分と $x$ 軸の正の向きとで作られる角で,2つある。

次の図で $\sankaku{OPH}$ は $\text{PH}:\text{OP}:\text{OH}=1:2:\sqrt{3}$ の直角三角形であるから,$\kaku{POH}=30\Deg$ である。

半円上で $y$ 座標が $\dfrac{1}{2}$ であるもう1つの点をQとすると対称性から $\kaku{HOQ}=150\Deg$ と分かる。

したがって,$\theta=30\Deg,~150\Deg$
(2) $\cos\theta=\dfrac{1}{\sqrt{2}}$
【(2)の考え方と解答】
コサインは $x$ 座標を表すから,破線で引いた直線 $y=x$ と半円との交点(赤い点)を通るように,直線 $y=\dfrac{1}{\sqrt{2}}$ を引く。
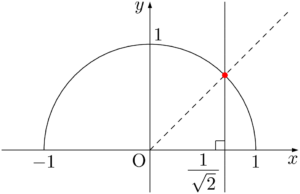
求める角 $\theta$ は,原点と赤い点を結んだ線分と $x$ 軸の正の向きとで作られる角である。
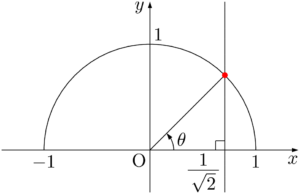
次の図で $\sankaku{OPH}$ は直角二等辺三角形であるから,$\kaku{POH}=45\Deg$ である。そもそも赤い点を考えた時点で直線 $y=x$ を引いていて,$\kaku{POH}=45\Deg$ であることは分かっていたりする。まさに「鶏が先か卵が先か」状態。
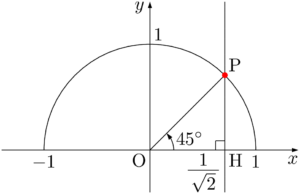
したがって,求める角 $\theta$ は $\theta=45\Deg$
コサインは $x$ 座標を表すから,破線で引いた直線 $y=x$ と半円との交点(赤い点)を通るように,直線 $y=\dfrac{1}{\sqrt{2}}$ を引く。

求める角 $\theta$ は,原点と赤い点を結んだ線分と $x$ 軸の正の向きとで作られる角である。

次の図で $\sankaku{OPH}$ は直角二等辺三角形であるから,$\kaku{POH}=45\Deg$ である。そもそも赤い点を考えた時点で直線 $y=x$ を引いていて,$\kaku{POH}=45\Deg$ であることは分かっていたりする。まさに「鶏が先か卵が先か」状態。

したがって,求める角 $\theta$ は $\theta=45\Deg$
(3) $\tan\theta=-\sqrt{3}$
【(3)の考え方と解答】
タンジェントは傾きを表すから直線 $y=-\sqrt{3}x$ を描こう。
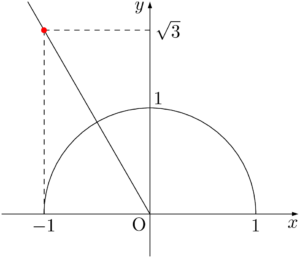
求める角 $\theta$ は,原点と赤い点を結んだ線分と $x$ 軸の正の向きとで作られる角である。
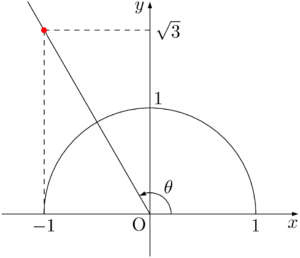
$\sankaku{POH}$ は $\text{OH}:\text{OP}:\text{PH}=1:2:\sqrt{3}$ の直角三角形であるから,$\kaku{POH}=60\Deg$ である。
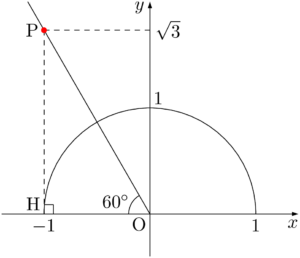
したがって,求める角 $\theta$ は $\theta=120\Deg$
タンジェントは傾きを表すから直線 $y=-\sqrt{3}x$ を描こう。

求める角 $\theta$ は,原点と赤い点を結んだ線分と $x$ 軸の正の向きとで作られる角である。

$\sankaku{POH}$ は $\text{OH}:\text{OP}:\text{PH}=1:2:\sqrt{3}$ の直角三角形であるから,$\kaku{POH}=60\Deg$ である。

したがって,求める角 $\theta$ は $\theta=120\Deg$
三角比を含む方程式の問題
問題$0\Deg\leqq\theta\leqq180\Deg$ のとき,次の等式を満たす $\theta$ を求めよ。
(1) $\sin\theta=\dfrac{1}{\sqrt{2}}$
(2) $\cos\theta=-\dfrac{1}{2}$
(3) $\tan\theta=-\dfrac{1}{\sqrt{3}}$
(1) $\sin\theta=\dfrac{1}{\sqrt{2}}$
(2) $\cos\theta=-\dfrac{1}{2}$
(3) $\tan\theta=-\dfrac{1}{\sqrt{3}}$

ヒロ
慣れてきたら,サクサク解いていこう。
【(1)の考え方と解答】
半円と直線 $y=\dfrac{1}{\sqrt{2}}$ を描こう。
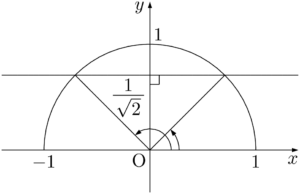
求める角 $\theta$ は上図の矢印で示した角であるから,$\theta=45\Deg,~135\Deg$
半円と直線 $y=\dfrac{1}{\sqrt{2}}$ を描こう。

求める角 $\theta$ は上図の矢印で示した角であるから,$\theta=45\Deg,~135\Deg$
(2) $\cos\theta=-\dfrac{1}{2}$
【(2)の考え方と解答】
半円と直線 $x=-\dfrac{1}{2}$ を描こう。
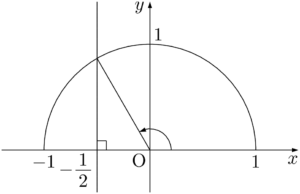
図より,$\theta=120\Deg$
半円と直線 $x=-\dfrac{1}{2}$ を描こう。

図より,$\theta=120\Deg$
(3) $\tan\theta=-\dfrac{1}{\sqrt{3}}$
【(3)の考え方と解答】
半円と直線 $y=-\dfrac{1}{\sqrt{3}}x$ を描こう。
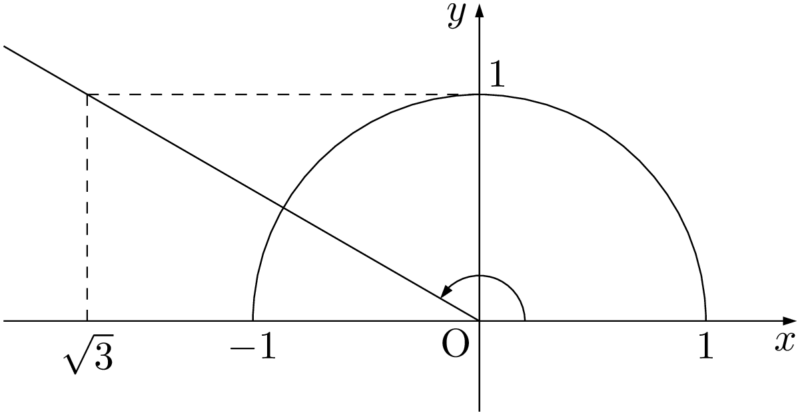
図より,$\theta=150\Deg$
半円と直線 $y=-\dfrac{1}{\sqrt{3}}x$ を描こう。

図より,$\theta=150\Deg$




















